Adding and Subtracting Radical Expressions With Square Roots and Cube Roots
Summary
TLDRThis lesson covers the addition, subtraction, and multiplication of radical expressions. It emphasizes how like terms are essential for adding or subtracting radicals and demonstrates the process of simplifying square and cube roots. The video provides several examples of combining radicals, breaking them down using perfect squares or cubes, and solving equations with distributed terms. Through various problem-solving steps, the video illustrates the importance of simplifying radicals and recognizing when terms can be combined, concluding with an advanced example involving the multiplication of conjugates and expanded expressions.
Takeaways
- 🔢 You can add or subtract radical expressions if they have the same radicals (like terms), such as combining 4√5 + 6√5 into 10√5.
- ❌ Expressions like 4√3 + 6√5 cannot be combined because the radicals are different.
- ➕ When adding or subtracting radical expressions with the same radical, only the coefficients are combined, like simplifying 7√2 - 3√2 + 5√2 into 9√2.
- 🟢 Simplifying radicals can make expressions combinable, such as breaking down √8 and √18 to form like terms √2, allowing the expressions to be combined.
- ✂️ Radicals like √12, √27, and √48 can be simplified into common radicals (like √3), which allows terms to be combined, yielding a result like 9√3.
- 🧮 Cube roots can be handled similarly, and simplification to like terms (such as cube root of 2) makes combining expressions possible.
- 🔄 Distributive property applies when multiplying radical expressions, such as in (√3)(7 + √3), which simplifies through distribution.
- 🧩 Multiplying conjugates (like 4 - √6 and 4 + √6) eliminates the middle terms, simplifying the result.
- 📐 For expressions like (2 + √3)², fully expanding by using FOIL helps combine the middle terms and results in simplified answers.
- 🔢 Complex problems involving radicals raised to powers can be simplified step-by-step using FOIL and multiplication, as shown with (4√3 + 2)³.
Q & A
What is the sum of 4√5 and 6√5?
-Since both terms have the same radical (√5), you can add the coefficients, 4 and 6. The result is 10√5.
Why can't you add 4√3 and 6√5?
-You can't add 4√3 and 6√5 because their radicals (√3 and √5) are different. You can only combine terms with the same radical.
How would you simplify the expression 7√2 - 3√2 + 5√2?
-Since all the terms have the same radical (√2), you can combine the coefficients. 7 - 3 + 5 equals 9, so the answer is 9√2.
How do you simplify 3√8 - 5√18?
-First, simplify the radicals: √8 becomes 2√2, and √18 becomes 3√2. After that, 3(2√2) = 6√2 and 5(3√2) = 15√2. Finally, subtract: 6√2 - 15√2 = -9√2.
What is the simplified form of 4√12 + 3√27 - 2√48?
-Simplify the radicals: √12 becomes 2√3, √27 becomes 3√3, and √48 becomes 4√3. Then, the expression becomes 8√3 + 9√3 - 8√3. The result is 9√3.
How do you simplify cube roots in expressions like 16^(1/3), 54^(1/3), and 128^(1/3)?
-You break the numbers down into perfect cubes. For example, 16 = 8 * 2, 54 = 27 * 2, and 128 = 64 * 2. Simplify the cube roots, and since all terms share a common radical (³√2), combine the coefficients.
What is the result of multiplying √3 by (7 + √3)?
-Distribute √3: √3 * 7 = 7√3, and √3 * √3 = 3. So, the final answer is 7√3 + 3.
How do you simplify the expression 4√5 * √7 - √3?
-First, multiply 4√5 by √7, which gives 4√35. Then multiply 4√5 by √3, which gives √15. The final expression is 4√35 - √15.
What is the result of multiplying conjugates like (4 - √6)(4 + √6)?
-The middle terms cancel, leaving only 4² - (√6)². This simplifies to 16 - 6, which equals 10.
How do you expand and simplify (5 + √2)²?
-First, apply the distributive property: (5 + √2)(5 + √2). This results in 25 + 10√2 + 2, which simplifies to 27 + 10√2.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
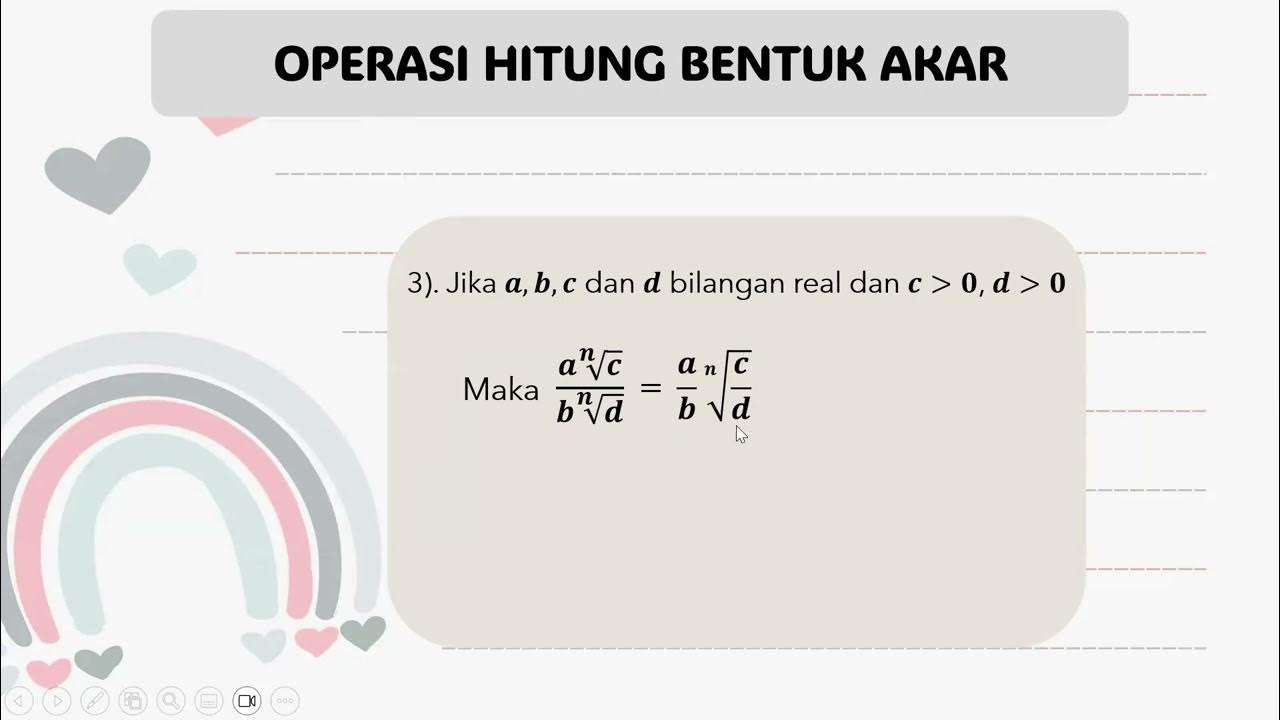
Asinkronus Topik Bentuk Akar W 2

BENTUK AKAR Kelas 10 Kurikulum Merdeka

As Quatro Operações Básicas da Matemática - Matemática 2º Ano - 22/11/2021

Translating Real-life Situations to Algebraic Expressions | 1st Quarter Grade 8 Matatag Revised K-12

Komposisi Fungsi Part 1 - Operasi Aljabar Pada Fungsi [ Matematika Wajib Kelas X ]

02.3. Sifat Sifat Penting Bilangan Riil Bagian 2
5.0 / 5 (0 votes)