How To Solve Any Projectile Motion Problem (The Toolbox Method)
Summary
TLDRIn this video, Jesse Mason tackles a classic projectile motion problem, focusing on calculating range, peak height, and velocity for a projectile launched from uneven ground. Using kinematic equations, Mason walks viewers through determining time, horizontal and vertical displacement, velocity components, and the trajectory's peak. He highlights the importance of breaking down motion into horizontal and vertical components and uses trigonometry and the quadratic formula to solve the problem. This tutorial emphasizes the need for a 'toolbox' of equations when approaching projectile motion challenges.
Takeaways
- 📐 Projectile motion problem involves determining the range, peak height, and velocity over time.
- 🖼️ The initial setup includes drawing a diagram of a projectile launched from a cliff at a 20° angle with an initial speed of 30 m/s.
- 📏 The projectile starts at an initial height of 100 meters, and gravity is set at -9.8 m/s².
- 🔄 The key unknowns are the horizontal range (x), the maximum vertical height (y-max), and the velocity at 2 seconds post-launch.
- 🔧 To solve, use kinematic equations separately for x and y directions, assuming no air resistance.
- ⏲️ The time of impact is solved using the quadratic formula, yielding a positive value of 5.68 seconds.
- 🏁 The horizontal range of the projectile upon impact is calculated to be 160.1 meters.
- 📊 The projectile reaches its peak height of 105.4 meters at 1.05 seconds after launch.
- 📉 At 2 seconds, the projectile’s velocity is 29.7 m/s with a downward angle of 18.3 degrees.
- 🔨 Using a toolbox of equations simplifies projectile motion analysis, making the process more systematic and organized.
Q & A
What is the main focus of this Teach Me installment?
-The main focus is solving a classic projectile motion problem involving an angled launch from uneven ground.
What are the key parameters given in the problem?
-The key parameters include the initial vertical displacement (height of the cliff: 100 meters), the magnitude of the launch velocity (30 meters per second), and the launch angle (20 degrees).
What is the first step in solving the projectile motion problem?
-The first step is to draw a diagram illustrating the cliff, the level ground below, the cannon's initial position, and the projectile's trajectory.
How is the acceleration due to gravity represented in the problem?
-The acceleration due to gravity is represented by the value -9.8 meters per second squared, since the positive y-axis is aligned upwards and gravity acts downward.
Which equations are used to solve for the projectile’s range and peak height?
-The kinematic equations for displacement and velocity in both the x- and y-directions are used. Specifically, equation (1) is used to calculate the horizontal displacement (range), and equation (3) is used to calculate the vertical displacement (peak height).
How is time calculated for when the projectile hits the ground?
-Time is calculated by solving equation (3) for vertical displacement (y = 0) using the quadratic formula. The positive time value of 5.68 seconds is used.
How is the range of the projectile determined?
-The range is determined by plugging the calculated time of 5.68 seconds into equation (1), yielding a horizontal displacement of 160.1 meters.
How is the peak height of the projectile determined?
-The peak height is determined by first calculating the time at which the vertical velocity is zero (t = 1.05 seconds) using equation (4), and then inserting this time into equation (3), which gives a peak height of 105.4 meters.
How is the velocity 2 seconds after launch calculated?
-The velocity 2 seconds after launch is calculated by using equation (2) for the horizontal component (v-sub-x = 28.19 m/s) and equation (4) for the vertical component (v-sub-y = -9.34 m/s).
How is the magnitude and direction of the velocity 2 seconds after launch determined?
-The magnitude of the velocity is determined using Pythagoras' Theorem, yielding 29.70 meters per second. The direction is calculated using the inverse tangent of the velocity components, giving an angle of 18.3 degrees below the horizontal.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Projectile Motion Part II | Quarter 4 Grade 9 Science Week 2 Lesson
Gerak Parabola • Part 3: Contoh Soal Gerak Parabola Dimulai dari Ketinggian Tertentu

How Do Horizontally Launched Projectiles Behave? | Physics in Motion

Projectile Motion: Finding the Maximum Height and the Range

S9Q4W2 | Part 2: PROJECTILE MOTION
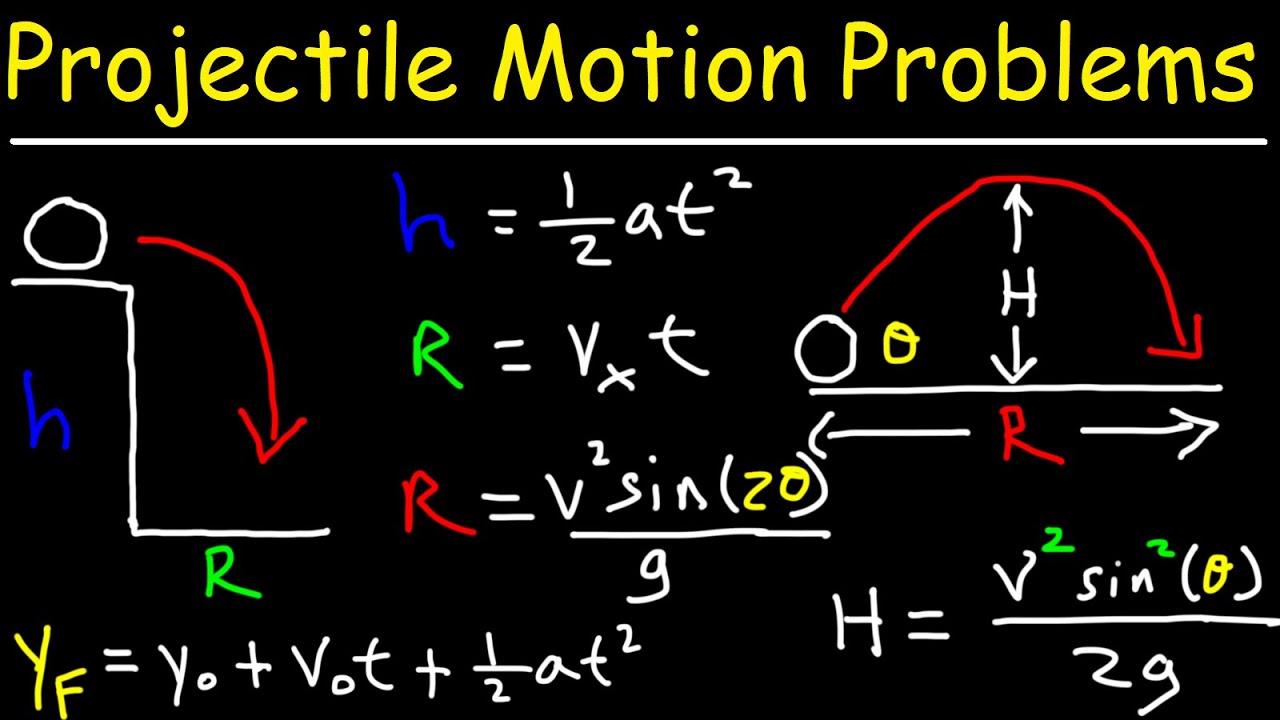
How To Solve Projectile Motion Problems In Physics
5.0 / 5 (0 votes)