S9Q4W2 | Part 2: PROJECTILE MOTION

Summary

This video lesson explores the concept of projectile motion launched at an angle, focusing on the relationship between the launch angle, height, and range of the projectile. Key topics include the horizontal and vertical components of motion, the effects of gravity, and complementary launch angles. The video also presents mathematical formulas for calculating maximum height and range, followed by a practical example involving a baseball hit at a 25° angle. Viewers will gain a deeper understanding of how launch angles impact the trajectory, height, and distance of projectiles in motion.

Takeaways

• 😀 The angle of release directly affects both the height and range of a projectile.
• 😀 A projectile follows a parabolic trajectory with horizontal and vertical components.
• 😀 The horizontal velocity of a projectile remains constant, while the vertical velocity is influenced by gravity.
• 😀 Gravity causes the vertical velocity to decrease as the projectile rises, become zero at its peak, and increase as it falls.
• 😀 The maximum range of a projectile occurs when launched at a 45° angle with respect to the horizontal.
• 😀 A launch angle of 75° results in the highest possible height for the projectile.
• 😀 Launch angles of 30° and 60° produce the same range and are referred to as complementary angles.
• 😀 The time to reach the highest point is equal to the time taken to return to the original launch height.
• 😀 The vertical component of velocity is zero at the peak height of a projectile's flight.
• 😀 To calculate the range and maximum height of a projectile, the initial velocity, angle, and acceleration due to gravity are used in specific formulas.

Q & A

What is the learning objective of this lesson?

The learning objective is to investigate the relationship between the angle of release and the height and range of a projectile.

What is the definition of projectile motion?

Projectile motion refers to the motion of a body that is launched into the air and is subject to gravitational force. It follows a parabolic trajectory and has horizontal and vertical components.

What is the horizontal component of projectile motion?

The horizontal component of projectile motion has zero acceleration, meaning the velocity is constant throughout the flight of the projectile.

What happens to the vertical velocity of a projectile as it rises?

As the projectile rises, the vertical velocity decreases because gravity opposes the motion.

What occurs at the maximum height of a projectile's flight?

At the maximum height, the vertical velocity becomes zero momentarily, and the projectile stops rising before it begins to fall back down.

What is the relationship between the angle of launch and the range of the projectile?

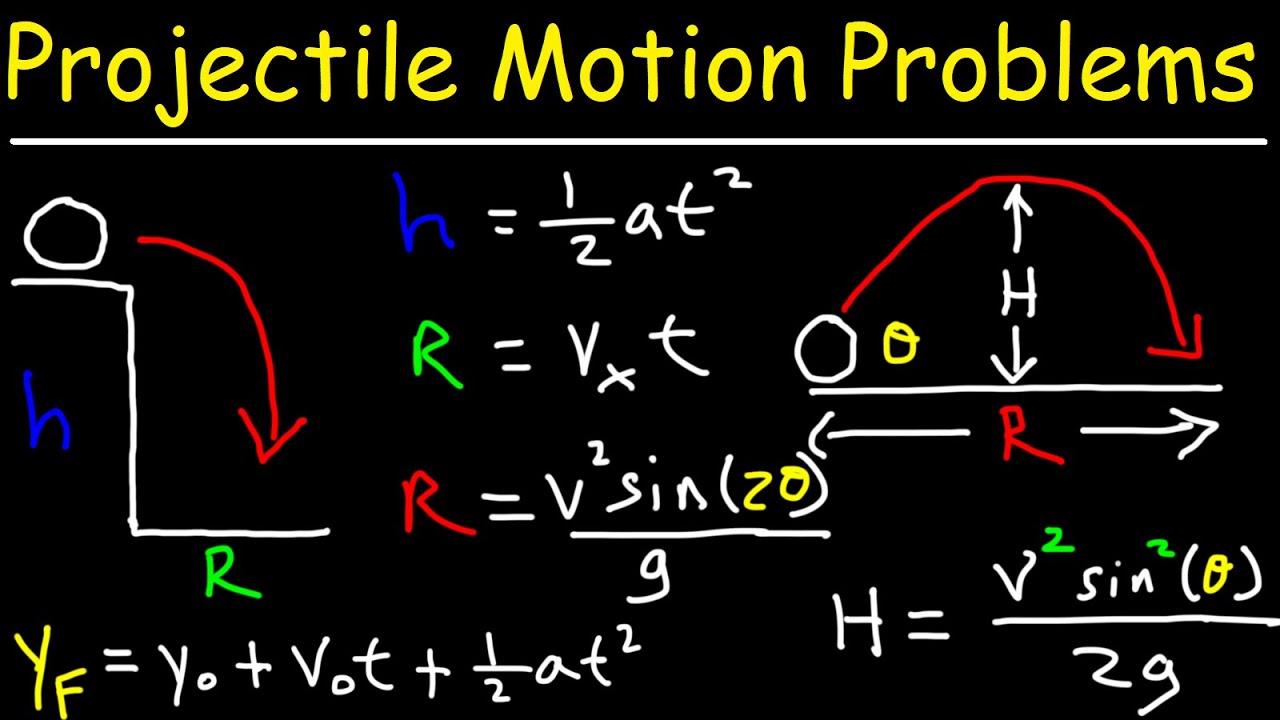
The range of a projectile is maximized when the angle of launch is 45 degrees. Angles of 30 and 60 degrees result in the same range because they are complementary angles that add up to 90 degrees.

Why do complementary angles (30 and 60 degrees) produce the same range?

Complementary angles, like 30 and 60 degrees, lead to the same range because the horizontal and vertical components of velocity are balanced in such a way that the total horizontal displacement is identical.

What is the effect of increasing the angle of launch on the vertical displacement?

As the angle of launch increases, the vertical displacement of the projectile also increases, meaning the projectile reaches a greater height.

What is the formula to calculate the maximum height of a projectile?

The maximum height can be calculated using the formula: (Vi * sin(θ))² / (2 * g), where Vi is the initial velocity, θ is the angle of launch, and g is the acceleration due to gravity.

What was the maximum height reached by the baseball in the example problem?

In the example problem, the maximum height reached by the baseball was 8.20 meters.

What formula is used to calculate the horizontal displacement (range) of a projectile?

The horizontal displacement (range) can be calculated using the formula: Vi * cos(θ) * t, where Vi is the initial velocity, θ is the angle of launch, and t is the total time of flight.

How much time did the baseball spend in the air in the example problem?

The baseball spent 2.59 seconds in the air in the example problem.