Projectile Motion Part II | Quarter 4 Grade 9 Science Week 2 Lesson

Summary

This video from the Maestro Techie YouTube channel dives into the intricacies of projectile motion, specifically focusing on the effects of the angle of launch on a projectile's range and height. The lesson begins with a review of the basic concepts of projectile motion, such as trajectory and the distinction between horizontal and vertical components. The video explains that while the horizontal velocity remains constant, the vertical velocity changes due to gravity's influence. It then explores the variables involved in launching a projectile at an angle and presents equations to solve problems related to projectile motion. The video highlights that the maximum range is achieved at a 45-degree angle and that a projectile launched at 30 degrees will have the same range as one launched at 60 degrees, due to these angles being complementary. An example problem is solved, calculating the maximum height and horizontal displacement of a baseball hit at a 25-degree angle with an initial velocity of 30 meters per second. The video concludes with a reminder of the impact of the angle of release on a projectile's trajectory, emphasizing the educational value of understanding these principles.

Takeaways

• 📚 Start with a review: If you missed the first week's lesson on projectile motion, check out the link in the description for an introduction to concepts like trajectory and the definition of projectile motion.
• 🚀 Understand the basics: A body in projectile motion follows a parabolic path with horizontal and vertical components, where the horizontal velocity is constant (acceleration equals zero) and the vertical acceleration is constant due to gravity (9.8 m/s²).
• 🔍 Analyze the game: Baseball is an example of projectile motion launched at an angle, illustrating how vertical velocity changes due to gravity's influence.
• 📈 Grasp the variables: In projectile launch at an angle, consider both the horizontal and vertical components of the motion.
• 📐 Initial conditions: An object projected from rest at an upward angle has an initial velocity that can be resolved into horizontal and vertical components.
• ⏱️ Time and velocity: The time it takes for an object to stop at its highest point is the same as the time it takes to return to the launch point, with the initial upward velocity being equal to the final velocity when it returns to its original height.
• 📐 Equations for solving: Learn and apply the equations for projectile motion to solve problems involving range, maximum height, and horizontal displacement.
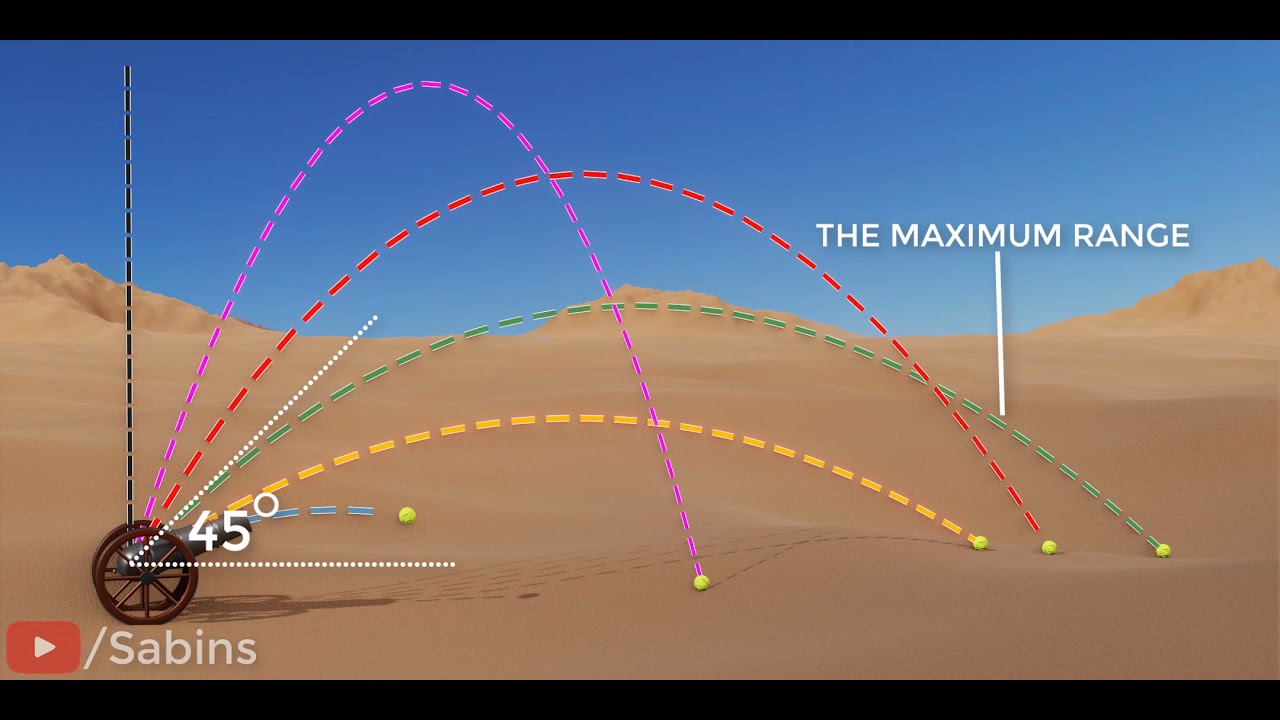
• 🎯 Optimal angle for range: The greatest range is achieved when the projectile is launched at a 45-degree angle to the horizontal.
• 📏 Complementary angles: Angles of 30 and 60 degrees are complementary and result in the same range, as do 15 and 75 degrees.
• 📈 Vertical displacement: As the angle of launch increases, the vertical displacement of the projectile also increases.
• ⏰ Time to reach max height: The time to reach the maximum height is half of the total time of flight.
• 📝 Example problem: For a baseball hit at an angle of 25 degrees with a velocity of 30 m/s, use the given formulas to calculate the maximum height and horizontal displacement of the ball.

Q & A

What is the general trajectory of a projectile in motion?

A projectile in motion follows a parabolic trajectory, which is the result of the combination of its horizontal and vertical components of motion.

What is the acceleration of the horizontal component of projectile motion?

The acceleration of the horizontal component of projectile motion is zero, as there are no forces acting in the horizontal direction once the projectile is launched.

What is the acceleration due to gravity and what is its value in meters per second squared?

The acceleration due to gravity is the constant acceleration that acts on the vertical component of projectile motion, and its value is 9.8 meters per second squared.

In the context of projectile motion, what is the term for the initial speed of the object when it is launched?

The initial speed of the object when it is launched is referred to as the initial velocity, which can be resolved into horizontal and vertical components.

What is the relationship between the angle of launch and the time it takes for a projectile to reach its highest point?

The time it takes for a projectile to reach its highest point is the same amount of time it takes to return to the point from which it was launched, regardless of the angle of launch.

What is the maximum range achieved by a projectile launched at an angle?

The maximum range of a projectile is achieved when it is launched at an angle of 45 degrees with respect to the horizontal.

What are complementary angles in the context of projectile motion, and how do they relate to range?

Complementary angles in projectile motion are two angles that add up to 90 degrees, such as 30 and 60 degrees. A projectile launched at one of these angles will have the same range as if it were launched at the other angle.

What is the formula used to calculate the maximum height reached by a projectile?

The formula to calculate the maximum height (h) reached by a projectile is h = (v_i * sin(θ))^2 / (2 * g), where v_i is the initial velocity, θ is the angle of launch, and g is the acceleration due to gravity.

How is the horizontal displacement or range of a projectile calculated?

The horizontal displacement or range (R) of a projectile is calculated using the formula R = v_i * cos(θ) * t, where v_i is the initial velocity, θ is the angle of launch, and t is the total time of flight.

What happens to the vertical velocity of a projectile at its highest point?

At the highest point of its trajectory, the vertical velocity of a projectile is momentarily zero because it momentarily stops before starting to fall back down due to gravity.

What is the significance of the angle of launch in determining the range and height of a projectile?

The angle of launch significantly affects both the range and height of a projectile. A higher angle increases the vertical displacement, while a 45-degree angle maximizes the range. Complementary angles result in the same range due to symmetry in the projectile's trajectory.

How does the direction of gravity influence the vertical velocity of a projectile?

The direction of gravity, which is downward, opposes the upward motion of a projectile, causing the vertical velocity to decrease as the projectile rises. Conversely, as the projectile falls back to the ground, the direction of gravity aids its motion, increasing the vertical velocity.

Outlines

00:00

📚 Introduction to Projectile Motion at an Angle

This paragraph introduces the topic of projectile motion launched at an angle, which is the focus of the Grade 9 science quarter for week 2. It sets the learning objective to investigate the relationship between the angle of release and the projectile's height and range. The paragraph also recaps the basic concepts of projectile motion, such as trajectory and the parabolic path created by the combination of horizontal motion with constant velocity and vertical motion with constant acceleration due to gravity. The example of a baseball game is used to illustrate these concepts, highlighting how the vertical velocity of the projectile changes due to gravity's influence.

05:01

🔍 Variables and Equations for Projectile Launch

This section delves into the variables involved in launching a projectile at an angle, emphasizing the distinction between the horizontal and vertical components of motion. It explains that an object projected from rest at an upward angle will have an initial velocity that can be resolved into horizontal and vertical components. The horizontal velocity remains constant, while the vertical velocity changes due to gravity. The paragraph also discusses the time it takes for the object to stop at its highest point and return to the launch point, and how the initial and final vertical velocities are of the same magnitude. Several equations are introduced to solve problems related to projectile motion at an angle, including those for maximum height and horizontal displacement (range).

10:04

🏞️ Angles for Maximum Range and Height

This paragraph explores the optimal angles for achieving maximum range and height in projectile motion. It reveals that a 45-degree angle results in the greatest range, while a 75-degree angle leads to the maximum height. The concept of complementary angles (30 and 60 degrees) is introduced, showing that they yield the same range. The paragraph also explains how the angle of launch affects the projectile's vertical displacement and the time it takes to reach the maximum height. An example problem is presented, where a baseball player hits a home run, and the video demonstrates how to calculate the maximum height reached by the ball and the horizontal displacement using the given launch angle and velocity.

🎓 Conclusion and Acknowledgment

The final paragraph wraps up the lesson on projectile motion, summarizing the key takeaway that the angle of release impacts both the range and height of a projectile. It reiterates the significance of a 45-degree angle for maximum range and provides a brief overview of the calculations performed in the example problem. The video concludes with a call to action for viewers to like, share, and subscribe for updates on future lessons. It also includes a shout out to specific individuals and groups, acknowledging their contribution to the video's success.

Keywords

💡Projectile Motion

Projectile motion is the study of an object's motion when it is launched into the air and moves under the influence of gravity alone. It is a key concept in physics and is central to the video's theme. In the script, it is used to describe the parabolic trajectory of an object, such as a baseball, when it is thrown or hit at an angle.

💡Trajectory

Trajectory refers to the path that an object follows through space as a result of its initial motion and the forces acting upon it. In the context of the video, the trajectory is parabolic for a projectile in motion, which is a fundamental concept for understanding how the angle of release affects the range and height of the projectile.

💡Horizontal and Vertical Components

These are the two separate components of motion that make up projectile motion. The horizontal component has a constant velocity with zero acceleration, while the vertical component experiences a constant acceleration due to gravity. The script explains that understanding these components is crucial for analyzing the motion of a projectile, such as a baseball in flight.

💡Acceleration Due to Gravity

Acceleration due to gravity is the constant acceleration that any object experiences when in free fall, which is approximately 9.8 meters per second squared on Earth. The script mentions this as the constant acceleration affecting the vertical component of a projectile's motion, causing it to rise, momentarily stop at its peak, and then fall back down.

💡Angle of Release

The angle of release is the angle between the horizontal and the initial velocity vector of the projectile when it is launched. The video discusses how this angle is critical in determining the range and maximum height a projectile will achieve. For instance, a 45-degree angle is shown to result in the greatest range.

💡Range

Range in the context of projectile motion is the horizontal distance traveled by the projectile from the point of launch until it returns to ground level. The script uses the term to illustrate that the range is maximized when the projectile is launched at a 45-degree angle, which is a key takeaway for students learning about projectile motion.

💡Maximum Height

The maximum height is the highest point reached by a projectile in its trajectory under the influence of gravity. The script explains that the maximum height can be calculated using the initial velocity and the angle of release, and it is different for different angles, with a 75-degree angle resulting in the maximum height in the given examples.

💡Complementary Angles

Complementary angles are two angles that add up to 90 degrees. In the context of the video, angles of 30 and 60 degrees are complementary because they sum to 90 degrees. The script points out that projectiles launched at complementary angles have the same range, which is an important concept in understanding projectile motion.

💡Initial Velocity

Initial velocity is the speed at which an object starts moving, in a specific direction, when it is launched. The script uses the term to describe the starting speed of the baseball when it is hit, which is a critical factor in determining the projectile's trajectory and the time it takes to reach its maximum height.

💡Time of Flight

Time of flight is the total time a projectile spends in the air from the moment it is launched until it lands. The video explains that the time it takes for a projectile to reach its highest point is half of the total time of flight, which is essential for understanding the overall motion of the projectile.

💡Baseball

In the script, baseball serves as a practical example of projectile motion. It is used to illustrate the concepts of trajectory, angle of release, and how these factors influence the horizontal and vertical components of the ball's motion. The video discusses a scenario where a baseball player hits a home run, providing a real-world application of the principles being taught.

Highlights

Investigate the relationship between the angle of release and the height and range of the projectile.

Projectile motion has a parabolic trajectory with horizontal and vertical components.

Horizontal component of projectile motion has zero acceleration, while vertical component has constant acceleration due to gravity (9.8 m/s²).

Baseball is an example of projectile motion launched at an angle.

Vertical velocity of a projectile decreases as it rises due to gravity, is zero at the maximum height, and increases as it falls back down.

Initial velocity of a projectile launched at an angle can be resolved into horizontal and vertical components.

Horizontal velocity is constant, while the vertical velocity changes due to gravity.

Time taken to reach the highest point is the same as the time taken to return to the launch point.

The initial upward velocity is the same magnitude as the final velocity when the projectile returns to its original height.

The angle that results in the greatest range is 45 degrees.

The angle that results in the maximum height is 75 degrees.

Projectiles launched at 30 and 60 degrees have the same range due to being complementary angles.

As the angle of launch increases, the vertical displacement of the projectile also increases.

At the highest point, the vertical component of velocity is zero, and the time to reach it is half the total flight time.

Example problem: Calculating the maximum height and horizontal displacement of a baseball hit at an angle of 25 degrees with a velocity of 30 m/s.

Formula for maximum height: VI * sin(Theta)^2 / (2 * g).

Formula for horizontal displacement (range): VI * cos(Theta) * time.

Total time of flight can be calculated using VI * sin(Theta) / g.

The final calculated maximum height reached by the baseball is 8.20 meters, and the horizontal displacement is 70.42 meters.

Transcripts

good day students welcome back to

Maestro techie YouTube channel let us

continue our discussion if you haven't

watched our week 1 video Lesson about

the horizontal and vertical motions of a

projectile check out the link in the

description box below we are now going

to have Grade 9 science quarter for week

2 lesson which is all about projectile

motion launched at an angle here's our

learning objective investigate the

relationship between the angle of

release and the height and range of the

projectile so get ready to learn this

lesson and keep on watching

[Music]

from the previous lesson you are

introduced to the basic concepts of

projectile motion such as trajectory and

and the definition of projectile motion

itself a body in projectile motion has

been established to have a parabolic

trajectory with a horizontal and

vertical components the horizontal

component of a projectile motion has the

acceleration equal to zero since the

velocity is constant on the other hand

the vertical component of acceleration

is constant which is acceleration due to

gravity and that is always equal to 9.8

meter per second squared therefore

projectile motion is the combination of

horizontal motion with constant velocity

and vertical motion with constant

acceleration take a look at this are you

familiar with this game

yes baseball this is an example of

projectile motion launched at an angle

for angle launch projectile horizontal

velocity or VX is still constant while

the vertical velocity can be described

in three parts first from the picture as

you observed

the projectile rises from point A to

point B the vertical velocity or v y is

decreasing this is because the direction

of gravity is opposite to the projectile

motion next as the projectile reaches

the maximum height which is the point B

it momentarily stops causing a vertical

velocity or v y equal to zero and third

when it returns back to the ground from

point B to point C it agrees to the

direction of gravitational force hence

Vertical Velocity is increasing

so when the vertical velocity of the

baseball as it rises to the air

decreases due to the opposing direction

of gravity towards the motion when the

baseball reaches the maximum height it

momentarily stops causing the vertical

velocity to be zero when it reaches to

the ground its vertical velocity

increases since the direction of the

baseball's motion is the same with

gravity take note of that class

now take a look at the variables

involved in projectile launch at an

angle

we have here the horizontal component

and the vertical component

[Music]

next we have the facts about projectile

launched at an angle first up an object

is projected from rest at an upward

angle Theta just like this scenario the

ball started from rest where stiff and

carry is holding the ball

second

its initial velocity can be resolved

into two components as you can see we

have the horizontal and the vertical

component third the horizontal velocity

is constant due to gravity a constant

horizontal velocity that moves in the

same direction as the launch the

acceleration of which is zero fourth the

amount of time the object takes to come

to a stop at its highest point is the

same amount of time it takes to return

to where it was launched from

and lastly the initial velocity upward

will be the same magnitude as the final

velocity when it returns to its original

height so these are the facts about

projectile launched at an angle next

here are some of the equations that may

help you solve problems involving

projectile launched at an angle

let's proceed

take a look at this photo class what can

you say

which angle results in the greatest

range

when we say range it is the horizontal

displacement and as you can see the

farthest range is in the 45 degrees

angle next question

which angle results in the maximum

height

hmm

as you can see it is the 75 degrees

angle

how would you compare the distance

traveled by projectile launched at 30

and 60 degrees as you can see they have

the same range same as 15 and 75 they

have the same range

this scenario that I have shown you is

also an example of projectile motion

launch at an angle and these are the

possible results if you launch an object

at different angle take note class angle

that is usually represented by Theta is

a numerical value in degrees expressing

the orientation of a projectile to be

from to sum it up class the angle of

release affects the range and height of

a projectile the maximum range is

achieved if the projectile is fired at

an angle of 45 degrees with respect to

the horizontal component an object

launched at an angle of 30 degrees will

also be the same if it is launched at 60

degrees

the angles 30 and 60 degrees are called

complementary angles because they add up

to 90 degrees

as the angle of launch increases the

vertical displacement of the projectile

will also increase at the highest point

the vertical component of velocity is

zero and the time to reach the maximum

height is half of the total time of

flight now let us have an example

problem

a baseball player leads off the game and

hits a long home run the ball leaves the

bat at an angle of 25 degrees with a

velocity of 30 meter per second let us

find the maximum height reached by the

ball and the horizontal displacement of

the boat let us illustrate the problem

as you can see we have an angle of 25

degree and a velocity of 30 meter per

second we are looking for the maximum

height reached by the ball and the

horizontal displacement or range or DX

of the ball let us try to solve this

problem here are the given our initial

velocity or VI which is equal to 30

meter per second our degree of angle

which is 25 degrees acceleration due to

gravity which is 9.8 meter per second

squared the formula that we are going to

use is VI times sine Theta squared

divided by twice the acceleration due to

gravity now let's substitute the given

to our formula d y is equal to our VI

which is 30 meter per second and sine

Theta which is sine 25 degrees do not

forget to square it to itself divided by

2 times 9.8 meter per second squared

multiplying these two quantities and

squaring it we have the product of

160.745 and so on meter squared per

second squared divided by the product of

2 and 9.8 and that is 19.6 meter per

second squared let us divide this two

the quotient

8.20 and as you can see we have to

simplify the units let's cancel out

and the remaining unit is meter

therefore our final answer or the

maximum height reached by the ball is

8.20 meters

now let us solve the second one

what is the horizontal displacement or

range of the bolt again here are our

given the formula that we are going to

use to find the DX is just multiplying v

i cosine Theta and the time as you can

see we do not have the value of time

therefore we have to solve the total

time to proceed in VX and this is the

formula that we are going to use so let

us solve it total time is equal to 2

times our VI and sine Theta all over the

acceleration due to gravity 30 times

sine 25 degrees is equal to

12.678 meter per second divided by of

course our acceleration due to gravity

12.678 divided by 9.8 times 2 we have

2.59 let us not forget to simplify our

unit by canceling

and our unit is seconds therefore the

total time traveled by the ball is 2.59

seconds now we can now solve for the

value of DX DX is equal to our VI cosine

Theta and the value of time multiplying

these three quantities our final answer

is

70.42 let us not forget to cancel the

units therefore our final answer is

70.42 meters and that ends our lesson

about projectile motion I hope you

learned something new today please give

this video a thumbs up share this to

your classmates and do not forget to

subscribe to keep you updated for our

next video Lesson comment down for a

shout out

shout out to Gabrielle balitas

Al-Qaeda Nifty red gien and mamirna

bigtas and all the grade 9 students of

San bartolome high school and also shout

out to all the science teachers of the

Vitae National High School thank you all

so much for watching see you on my next

video bye

[Music]