Understanding Bernoulli's Equation
Summary
TLDRThis video explains Bernoulli's equation, a fundamental concept in physics and engineering that describes the relationship between pressure, velocity, and elevation in fluid flow. It showcases real-world applications, including how planes generate lift, how liquid flows through pipes, and how devices like Venturi meters measure flow rates. The video also highlights limitations of the equation and its assumptions. Additionally, viewers are encouraged to sign up for CuriosityStream to access more educational content, including Nebula, a platform with exclusive content from top creators.
Takeaways
- 📚 Bernoulli's equation is essential for understanding fluid dynamics, describing the relationship between pressure, velocity, and elevation in a flowing fluid.
- ✈️ The equation helps explain phenomena like how planes generate lift and how liquid flows through a container.
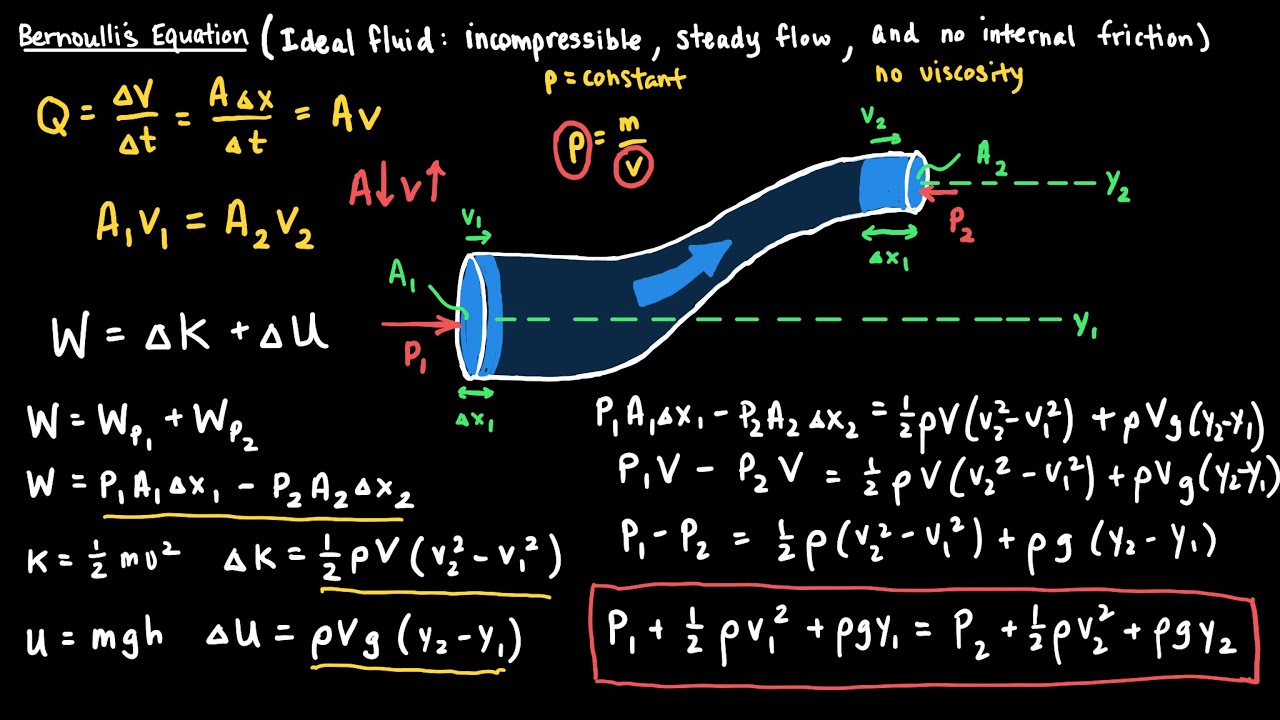
- 🔍 Bernoulli’s equation expresses the conservation of energy along a streamline, showing how pressure energy, kinetic energy, and potential energy remain constant.
- 📏 The equation compares fluid flow between two points and is often simplified for cases with negligible changes in elevation.
- ⚠️ Bernoulli’s equation assumes steady, incompressible, and inviscid flow, and these limitations must be considered when applying it.
- 🔬 The equation helps explain practical concepts like the design of Venturi meters and Pitot-static tubes, used for measuring fluid flow and velocity.
- 🛠️ Real-world applications include airplane lift, Bunsen burners, and measuring flow in pipes or tanks like a beer keg.
- 💡 The principle behind Bernoulli’s equation can seem counterintuitive: faster fluid flow leads to lower pressure, which is crucial in understanding fluid mechanics.
- 🎥 The video extends this explanation with more examples of Bernoulli’s principle on Nebula, a streaming service for educational content.
- 🌐 By signing up for CuriosityStream, viewers gain access to Nebula, which offers ad-free videos from educational creators, including the Efficient Engineer channel.
Q & A
What is Bernoulli's equation and why is it important?
-Bernoulli's equation is a fundamental equation in physics and engineering that describes the relationship between pressure, velocity, and elevation in a flowing fluid. It's important because it helps explain a wide range of phenomena, including how planes generate lift and how fluid moves through pipes.
What are the three terms in Bernoulli's equation?
-The three terms in Bernoulli's equation are static pressure, dynamic pressure, and hydrostatic pressure. Static pressure is the pressure of the fluid, dynamic pressure represents the fluid’s kinetic energy per unit volume, and hydrostatic pressure is the pressure exerted by the fluid due to gravity.
How does Bernoulli's equation relate to the conservation of energy?
-Bernoulli's equation can be viewed as a statement of the conservation of energy, indicating that the sum of pressure energy, kinetic energy, and potential energy remains constant along a streamline. This allows for the analysis of fluid behavior in various applications.
What assumptions are made when applying Bernoulli's equation?
-The assumptions made when applying Bernoulli's equation include that the flow is steady (not varying with time), inviscid (neglects viscosity), and incompressible (typically valid for liquids, but not always for gases at high velocities). These assumptions are important for the equation's accuracy.
How is Bernoulli's equation applied to fluid flow through a pipe with varying diameters?
-In a pipe with a change in diameter, Bernoulli’s equation shows that as the fluid flows from a larger to a smaller diameter, its velocity increases and its pressure decreases. This is explained by the conservation of energy and the continuity equation, which maintains a constant mass flow rate.
What is Bernoulli's Principle, and how does it relate to velocity and pressure?
-Bernoulli’s Principle states that an increase in fluid velocity must be accompanied by a decrease in pressure for horizontal flow. This principle follows from the conservation of energy, where the energy required to increase velocity comes at the expense of pressure energy.
How does Bernoulli's Principle explain how planes generate lift?
-Bernoulli’s Principle explains that as air flows faster over the top of a plane's wing (airfoil), it creates a region of lower pressure compared to the slower air underneath the wing, generating lift due to the pressure difference.
What role does Bernoulli's equation play in devices like the Pitot-static tube?
-In a Pitot-static tube, Bernoulli's equation is used to measure the velocity of a fluid by comparing stagnation pressure (where fluid velocity is zero) and static pressure, allowing the calculation of fluid speed in applications like aircraft airspeed measurement.
How is Bernoulli's equation used to calculate the flow rate through a Venturi meter?
-In a Venturi meter, Bernoulli’s equation is used to calculate the flow rate by measuring the pressure drop across a converging section of a pipe. The flow rate is determined using the cross-sectional area, fluid density, and pressure measurements at two points.
What are the limitations of Bernoulli's equation, and when can it not be applied?
-The limitations of Bernoulli’s equation arise from its assumptions: it cannot be applied to unsteady, viscous, or compressible flows. For cases where these assumptions don't hold, adapted versions of the equation must be used.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)