Fluidos em Movimento parte II

Summary

This video script explains the application of energy conservation principles to steady, incompressible, non-rotational fluid flow in a system. The focus is on a tube with two sections, each defined by pressure (P1, P2), velocity (V1, V2), and height (Y1, Y2). The script discusses how energy transformations occur between the sections, accounting for gravitational and pressure forces, and includes the use of Bernoulli's equation. Special cases like static fluids and horizontal pipes are addressed, highlighting the inverse relationship between velocity and pressure. The script demonstrates fundamental fluid dynamics concepts in practical scenarios.

Takeaways

• 😀 The script discusses the application of energy conservation to steady, incompressible, non-rotational fluid flow in a tube.
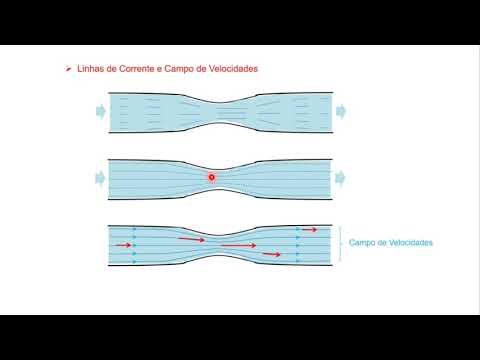
• 😀 The flow system is bounded by two transverse sections (1 and 2), with pressure (P1 and P2), velocity (V1 and V2), and height (Y1 and Y2) at these sections.
• 😀 The concept of stationary flow is emphasized, with the flow between sections 1 and 2 being treated as if it undergoes no significant changes in energy.
• 😀 Energy conservation is applied to the movement of a fluid element from section 1 to section 2, considering work done by pressure forces and gravity.
• 😀 The work done by gravitational forces is equal to the negative variation in gravitational potential energy of the fluid.
• 😀 The work done by pressure forces is represented as the force (P1) applied over the distance of the cross-section.
• 😀 The change in kinetic energy of the fluid is related to the difference in velocities between sections 1 and 2, using the equation for kinetic energy (½mv²).
• 😀 The script derives the expression for kinetic energy change in terms of pressure and velocity, resulting in a simplified Bernoulli equation.
• 😀 The principle of energy conservation results in an equation where the sum of pressure energy and kinetic energy remains constant along the flow.
• 😀 The derived Bernoulli equation can be applied to special cases such as horizontal tubes where height differences are negligible and velocity differences play a more prominent role in pressure variation.
• 😀 The script highlights that in regions of higher velocity, the pressure should be lower, demonstrating the inverse relationship between velocity and pressure in fluid dynamics.

Q & A

What is the main topic of the script?

The main topic of the script is the application of energy conservation to the steady, incompressible, non-rotational flow of a fluid through a pipe, specifically utilizing Bernoulli's equation to analyze fluid dynamics.

What are the two sections mentioned in the script for analyzing the fluid flow?

The two sections referred to in the script are section 1 and section 2, where the pressures (P1 and P2), velocities (V1 and V2), and heights (Y1 and Y2) are measured in relation to a horizontal reference plane.

What is meant by 'steady flow' in the context of this script?

Steady flow refers to the condition where the fluid's velocity and other properties do not change with time at any given point in the flow field.

How is the conservation of energy applied to the fluid system?

The conservation of energy is applied by considering the changes in kinetic energy, potential energy (due to gravity), and work done by pressure forces as the fluid flows between the two sections. The energy equation ultimately relates the velocity, pressure, and height at each section.

What does the equation derived in the script represent?

The equation derived represents the principle of energy conservation in fluid flow, specifically the relationship between the kinetic energy, potential energy, and work done by pressure forces. It is mathematically expressed as: P1 + 1/2 ρ V1^2 + ρ g Y1 = P2 + 1/2 ρ V2^2 + ρ g Y2.

What assumption is made about the fluid in this analysis?

The fluid is assumed to be incompressible, meaning its density does not change during the flow, and the flow is non-rotational, implying there are no vortices or rotational components in the flow.

Why is gravitational potential energy considered in the equation?

Gravitational potential energy is considered because the fluid's height at different sections affects the total energy. Changes in height contribute to the work done by gravity, which is reflected in the energy equation.

What does the script say about the relationship between pressure and velocity in a constricted pipe section?

The script explains that in a constricted section of the pipe, where the velocity increases, the pressure decreases. This is consistent with Bernoulli's principle, which states that an increase in the velocity of a fluid results in a decrease in pressure.

How does the principle of energy conservation relate to real-world fluid systems?

In real-world systems, the principle of energy conservation helps to predict and understand how fluid velocities, pressures, and heights interact. For example, it explains why fluid speed increases in narrow sections of a pipe and how pressure drops as velocity increases.

What simplification is made in the case of a horizontal pipe?

In the case of a horizontal pipe, the height terms (ρ g Y1 and ρ g Y2) can be disregarded because there is no change in elevation, simplifying the equation to P1 + 1/2 ρ V1^2 = P2 + 1/2 ρ V2^2.