Functions

Summary

This educational video script introduces the concept of functions in mathematics, explaining how to identify if a mapping is a function using mapping diagrams and the vertical line test. It covers one-to-one and many-to-one functions, function notation, and how to find the range and domain of a function. The script also discusses excluding values from the domain, composite functions, and finding inverse functions. It provides examples and step-by-step instructions for understanding and applying these mathematical concepts.

Takeaways

• 🔍 To determine if a mapping is a function, ensure each element in the domain maps to exactly one element in the range.
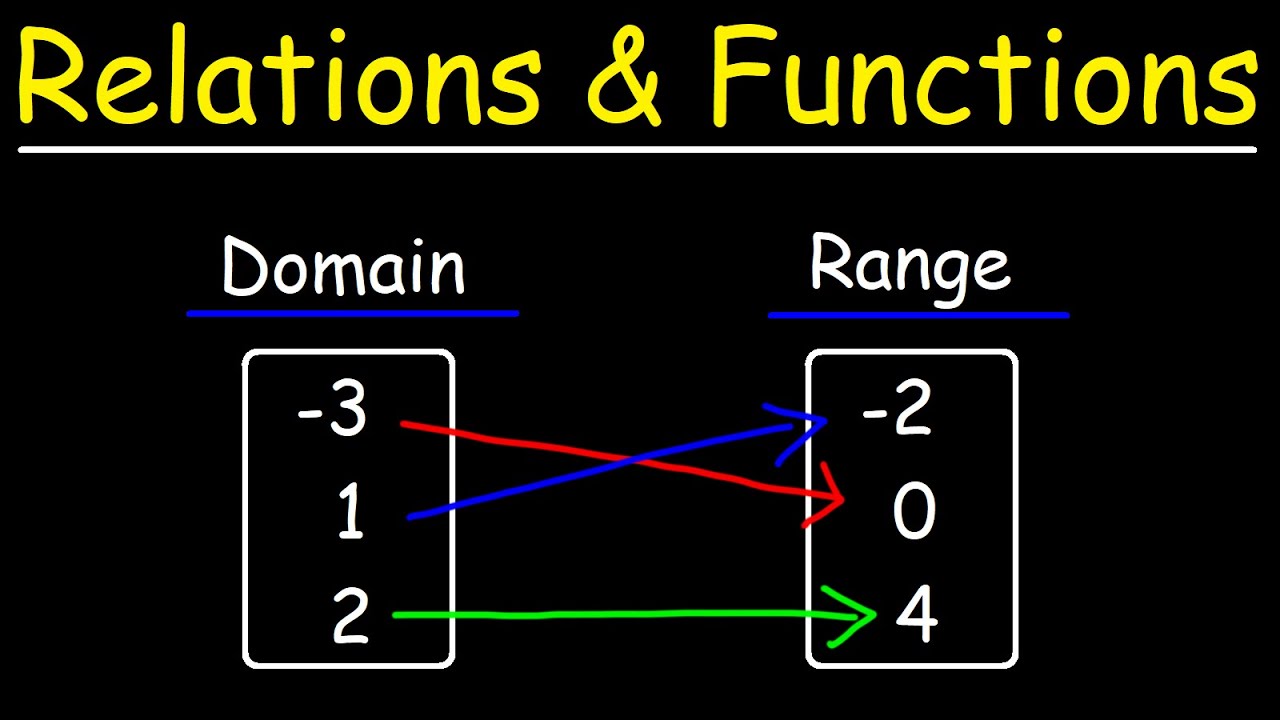
• 📊 Mapping diagrams and the vertical line test are useful tools to visualize whether a relationship is a function.
• 📐 A one-to-one function is where each element in the domain maps to a unique element in the range, while a many-to-one function has multiple elements in the domain mapping to the same element in the range.
• ❌ Diagrams where elements in the domain map to more than one element in the range, or vice versa, do not represent functions.
• 📝 Function notation, like \( f(x) \), is used to represent the rule by which an input is transformed into an output.
• 🔢 The domain of a function includes all possible input values, while the range consists of all possible output values.
• ⛔ Certain values, like zero in division or negative numbers in square roots, may need to be excluded from the domain as they lead to undefined operations.
• 🔄 Composite functions are created when one function's output becomes the input for another function, with the order affecting the final result.
• 🔄 The notation \( g(f(x)) \) indicates that function \( f \) is applied first, followed by function \( g \).
• 🔙 Inverse functions reverse the action of the original function; if \( f \) adds one, \( f^{-1} \) subtracts one.
• 📉 To find the inverse of a function, rewrite the function as \( y = \), swap \( x \) and \( y \), solve for \( y \), and use the notation \( f^{-1}(x) \).

Q & A

What is a function in mathematical terms?

A function is a mathematical relationship where each element of one set, called the domain, is associated with exactly one element of another set, called the range.

How can you determine if a mapping is a function using a mapping diagram?

A mapping is a function if each member of the first set (domain) is connected by exactly one arrow to an element of the second set (range), with no element in the second set being connected to more than one arrow.

What is the difference between a one-to-one function and a many-to-one function?

A one-to-one function is where each element in the domain maps to a unique element in the range, and each element in the range is mapped to by exactly one element from the domain. A many-to-one function allows multiple elements in the domain to map to the same element in the range.

How do you use the vertical line test to determine if a graph represents a function?

The vertical line test checks if any vertical line drawn on the graph intersects more than once with the graph. If it intersects only at one point for every vertical line, then the graph represents a function.

What is function notation and how is it used?

Function notation is a way to represent a function using a symbol, often a letter like 'f'. For example, if 'f(x)' represents a function, then 'f(5) = 10' means that when the input '5' is put into the function 'f', the output is '10'.

Can you explain the concept of domain and range in the context of functions?

The domain of a function is the set of all possible input values (x-values), while the range is the set of all possible output values (y-values). The domain is what you put into the function, and the range is what you get out of it.

Why are some values excluded from the domain of a function?

Values are excluded from the domain of a function if they lead to impossible operations, such as division by zero or taking the square root of a negative number, which are undefined in real number arithmetic.

What is a composite function and how is it formed?

A composite function is formed when one function is followed by another. For example, if you have functions f(x) and g(x), then the composite function g(f(x)) means you first apply f to x, then apply g to the result of f(x).

How do you find the composite function (g ∘ f)(x) given functions f(x) and g(x)?

To find the composite function (g ∘ f)(x), you first evaluate f(x) to get an output, then use that output as the input for g(x). The result is the value of (g ∘ f)(x).

What is an inverse function and how can you determine if a function has an inverse?

An inverse function is a function that reverses the effect of the original function. If applying the original function and then its inverse to a number yields the original number, and vice versa, then the function has an inverse. The notation for the inverse of a function f is f^(-1)(x).

How do you find the inverse of a given function algebraically?

To find the inverse of a function algebraically, you first write the function as y = f(x), then swap x and y to get x = f(y), and finally solve for y to express it in terms of x. This new expression is the inverse function, denoted as f^(-1)(x).

Outlines

00:00

📐 Introduction to Functions

The script begins with an introduction to the concept of functions in mathematics. It outlines the objectives of the lesson, which include understanding how to determine if a mapping is a function, using function notation, finding the range of a function, identifying values that may need to be excluded from the domain, finding composite functions, and determining inverse functions. The explanation emphasizes the importance of one-to-one and many-to-one relationships in functions and uses mapping diagrams to illustrate these concepts. It explains how a function can be identified by ensuring that each element of the first set maps to exactly one element of the second set. The script also introduces the vertical line test as a method to determine if a graph represents a function.

05:04

🔢 Function Notation and Operations

This section delves into function notation, explaining how a function is a set of rules for transforming one number into another. It uses the example of a doubling function, denoted as 'F', to demonstrate how function notation works. The script clarifies that if 'x' is the input, then '2x' is the output for the doubling function. It further explains how functions operate on all inputs and provides an example of a function that doubles and adds one. The concept of domain and range is introduced, with domain being the set of possible inputs and range being the set of possible outputs. The script also touches on values that may be excluded from the domain due to impossibilities such as division by zero or the square root of a negative number.

10:06

🔄 Composite Functions

The script moves on to discuss composite functions, which are created when one function is followed by another. It uses a graphical example to illustrate how the output changes based on the order in which functions are applied. The explanation includes a step-by-step process for finding composite functions, emphasizing the importance of the order of operations. The script also explains how the domain of one function (G) must align with the range of another function (F) when creating composite functions. It provides a practical example of finding the result of a composite function, 'f(g(x))', and clarifies the notation used for composite functions.

15:09

🔄 Inverse Functions

The final section of the script introduces inverse functions, which are functions that undo the operations of another function. It explains that if a function adds one, its inverse would subtract one. The script provides an example of two functions, F and G, and demonstrates how their inverses work. It outlines a step-by-step process for finding the inverse of a function, which includes writing the function as 'y =', swapping x and y, and solving for y to obtain the inverse function. The script concludes with an example of finding the inverse of a given function, 'f(x) = 6x + 4', and demonstrates how to apply the steps to arrive at the inverse function, 'f^(-1)(x) = (x - 4) / 6'.

Keywords

💡Function

In the context of the video, a function is a mathematical concept that represents a relationship between two sets, where each element of the first set (domain) is associated with exactly one element of the second set (range). The video explains that a function can be identified by using a mapping diagram or a graph with a vertical line test. Functions are crucial in understanding the transformations and operations that occur within mathematical equations, as they dictate the output for a given input.

💡Mapping Diagram

A mapping diagram is a visual tool used to determine if a relationship is a function. It illustrates the association between elements of two sets. In the video, it is used to show whether each element in the first set (domain) maps to exactly one element in the second set (range). If only one arrow leaves each member of the set, the relationship is a function, which can be either one-to-one or many-to-one, as demonstrated in the script with diagrams A and B.

💡One-to-One Function

A one-to-one function is a type of function where each input is mapped to a unique output. This means that different inputs will never produce the same output. The video uses a mapping diagram to illustrate this concept, where each element in the first set is connected to a distinct element in the second set, ensuring that the function is both injective (one-to-one) and surjective (onto).

💡Many-to-One Function

A many-to-one function is characterized by the fact that multiple inputs can map to the same output. This is demonstrated in the video through a mapping diagram where multiple elements from the first set are connected to the same element in the second set. This type of function is not one-to-one, as it does not meet the injectivity requirement.

💡Domain

The domain of a function refers to the set of all possible input values (x-values) for the function. The video explains that the domain is the set of numbers that can be used as inputs for a function without leading to impossible operations, such as division by zero or taking the square root of a negative number. The domain is depicted on the x-axis of a graph of a function.

💡Range

The range of a function is the set of all possible output values (y-values) that result from applying the function to its domain. In the video, it is mentioned that the range is the set of numbers produced by the function, which is depicted on the y-axis of a graph of a function. The range is determined by the function's operation and the domain from which it receives inputs.

💡Composite Function

A composite function is created when one function is followed by another. The video script provides an example where the function f(x) = 2x is followed by g(x) = x + 3, resulting in g(f(x)). The order of the functions is crucial, as changing the order changes the output, which is evident when the functions are applied in reverse order.

💡Inverse Function

An inverse function is a function that 'undoes' the action of another function. If a function adds one to a number, its inverse would subtract one. The video explains that the inverse function is denoted by f⁻¹(x) and that it can be found by reflecting the function over the line y = x on a graph. The script also outlines a step-by-step process for algebraically finding the inverse of a given function.

💡Vertical Line Test

The vertical line test is a graphical method to determine if a curve represents a function. If a vertical line intersects the curve at more than one point, then the curve does not represent a function, as a function requires each input to have exactly one output. The video script uses this test to confirm that a given graph is indeed a function by ensuring that a vertical line will only intersect the graph at one point.

💡Function Notation

Function notation is a way to express a function using a symbol, typically a letter like 'f' or 'g'. In the video, it is shown that if a function is defined to double a number and add one, it can be represented as f(x) = 2x + 1. This notation simplifies the expression of complex operations and allows for easy application of the function to different inputs.

Highlights

Introduction to the concept of functions and their properties.

Explanation of how to determine if a mapping is a function using a mapping diagram.

Definition of one-to-one and many-to-one functions with examples.

Use of the vertical line test to identify whether a graph represents a function.

Introduction to function notation and how to use it to represent a set of rules.

Example of how to find the range of a function using a graph.

Explanation of domain and range in the context of functions.

Discussion on values that may need to be excluded from the domain of a function.

Introduction to composite functions and how they are formed.

Example of how to calculate a composite function step by step.

Explanation of how to find the inverse of a function.

Step-by-step guide on how to derive the inverse function from a given function.

Graphical representation of an inverse function and its relationship to the original function.

Practical example of finding the inverse of a specific function.

Summary of the process for finding the inverse function, including changing variables and solving for y.

Final remarks on the importance of understanding functions, their properties, and operations.

Transcripts

hello everyone now we are going to our

new topic Which is

functions so at the end of this lesson

you will be able to determine whether a

mapping is a

function use function notation find the

range of a

function understand Which values may

need to be exclud from a domain find a

composite functions and last find

inverse

functions okay so first we need to

identify

functions relationship that are one to

one and many to one are functions a

mapping diagram makes it easy to desde

if it is a function or not If only one

arrow Leaves each member of the set then

the relationship is a function for

example look at these two

diagrams first diagram is diagram

a a is a function as each Element of the

first set maps to exactly one Element of

the second set it is a one to one

function As You can see one maps to two

two maps to three and three maps to

F diagram B is a function as each

Element of the first set maps to exactly

one Element of the second set since the

Elements in the second set have more

than Element From the first set map to

them It is called a many to one function

for example you can see that in diagram

B min2 and2 is maps to

F so they are called many to

One OK now we have diagram c and diagram

d c is not a function as each Element of

the first set maps to more than one

Element of the second set as you can see

in diagram c one maps to min1 and 1 that

means diagram c is not a

function now diagram D D is not function

either as at least one Element of the

first set maps to more than one Element

of the second set as you can see in

diagram d one maps to two and three So

it means diagram D is not a

function we can also use the vertical

Line test to decide if the graph Shows a

function or not it will only intersect

at one point if it is a function state

if it is one to one or many to one for

example look at this graph Wherever The

Red vertical line is placed on the graph

It will only intersect at one point

showing for example that one

1.5 maps to

2.5 So this is a

function it is an example of a one to

one

function next is function

notation a function is a set of rules

for turning one number into

Another You can see on the graph if we

put a number into a function It will

produce another

number so a letter can be used to

represent the rule if we call the

doubling function F Then if we Put in 5

to the function It will produce

10 F has operated on 5 to give 10 so we

write F of 5 equ to

10 if X is input then 2x is output that

is the doubling

function so we write f x equs to 2x or

we can use this notation

okay so in

graphic you can see that if we Put in x

2 f it will produce 2x

Ok

next a function operates on all of the

input if the function is double and add

One Then if 4x is input 8X + 1 is output

So if we Put in

4x to a function and the function is

double so we need to double 4x 4x get

double we get

8X and add one the function says so the

result the output of this function is

s + 1 topic is domain and

range okay so look at this

graphic the only the only Numbers The

function can use are one two F and seven

so we called The ers as

domain and set produced by the function

is 3 f si n so we call these numbers as

range so basically domain is the input

The Numbers that we Put in a into a

function and range is the the result we

get or the output we get from a

function so a graph of a function gives

a useful picture of the domain and range

for example these two graph you can see

that X Axis is the domain and yaxis is

the range so the domain cor

to the xxis and the range corresponds to

the

yxis we continue to values excluded from

the

domain some numbers cannot be used for

the domain as they lead to Impossible

operations these operations are usually

division by Zer we cannot Divide a

number by Zer or the square root of a

negative number there are no square root

of a negative

number ok so for example the function is

1/ X as I

can as I already ST before we cannot

Divide a number

exud

x from the domain of

F second example

is

FX root of

X the square root of a negative number

is not allow though is possible to soter

So

X smaller than Zero must be excluded

from the domain of

F next topic is composite

function so when one function is

followed by another the result is a

composite function

look at the graph if fx = 2x and GX = x

+ 3 then when we Put in two into F We've

got F because 2* 2 is 4 And if this

result this 4 we Put into G We've got

seven because

because 4 + 3 e=

7 if the Order of this functions is

change then the output is different for

example when we P in two to G first

We've got 5 because 2 + 3 is 5 and after

it we Put in 5 into F We've got 10

because 2 times 5 is

10 So if X is input then when we Put in

X to F We've got F of X after we we Put

in F of X to G weve got G of F of

x g of

FX is usually written without the square

brackets as

GF of X GF of X means do F first then

followed by G note that the domain of g

is the range of F in the same way f g of

X means do G first and then for follow

by

F for example weve got fx = x s and GX =

x +

2 and the question ask us to find f

G3 so as i state before

fgx means do G first so we need to do g

g of th

first that means we Put in 3 to the g

function so weve got 3+ 2 Which is 5

after We did

G3 we need to put in the result the

output of the G3 to the F function So it

become F of

5 so f squ i mean so 5 squ is equal to

25 so the result of f g of3 is

25 we continue to inverse

function the inverse function Andes

whatever has been done by the

function so So if the function is add

one then the inverse function is

subtract

one these functions are FX for example

FX Div by x + 1 add 1 and GX is x- 1

subtract 1 So if F is followed by G then

whatever number is in

is also the output because the G

function

und Everything that the the F

function

done So if X is the input then X is also

the

output so the function g is called The

the inverse of the function f the

inverse of F is the function that

und whatever F has done the notation f-

1 is used for the inverse of

F note that graphically f-1

X is a Reflection of f x in y equ

x but what if the inverse function is

not obvious

Oke So this following steps will help

you to find the inverse

function step one write the function as

y

equ Step Two change any X to y and any y

to x and last step is to make y subject

giving the inverse function and then use

the correct f- 1 x notation for

example find invers of the function

given

fx= 6x +

4 okay so the first step we need to do

is y the function as y equ what what we

got

fx 6x + 4 so we need to the function as

y e= 6x +

4 Next step two is to change any X to y

and change any y to

X so before we have y e= 6x + 4 and we

need to change y to x and X to y so

We've got X Equals to 6y +

4 last step is to make y the sub giving

the inverse function and then we use the

correct

f-1 X notation so before we

already do x equ= to 6 Y + 4 so to make

y The Subject we need to move this F To

The Other Side so weve got x- 4 equ to

6y and to remove the 6 from 6y we need

to

Divide so weve got Y = x- 4 Div 6 or y =

x-

4/6 after that We just need to change

the y to the f- 1x so the F Min So the

f- 1x is equal to x- 4// 6 so the

inverse function of fx = 6x + 4 is

f- 1x = x- 4 Div

6 oh

[Musik]