An Introduction to Stress and Strain

Summary

This video explores the fundamental concepts of stress and strain, using a solid metal bar under uniaxial loading as an example. Stress, measured in Pascals, is the internal force per unit area and can be normal or shear, affecting the body's response to external loads. Strain, a dimensionless quantity, describes deformation, such as the change in length of the bar. The video explains how stress and strain are calculated, their relationship through Hooke's Law and Young's Modulus, and the importance of understanding these concepts for predicting material failure and analyzing more complex scenarios like torsion and beam bending.

Takeaways

• 🔍 Stress and strain are fundamental in understanding how materials respond to external loads.
• 📚 Uniaxial loading is a scenario where all applied loads act along the same axis, causing a bar to stretch.
• ⚖️ Internal forces within a material develop to resist external forces, and these can be visualized by imagining a cut through the material.
• 📏 Stress is defined as the internal force per unit area, measured in Pascals (or Newtons per square meter in SI units).
• 🔑 The ability to calculate stress is crucial for predicting material failure, as it relates to the material's strength.
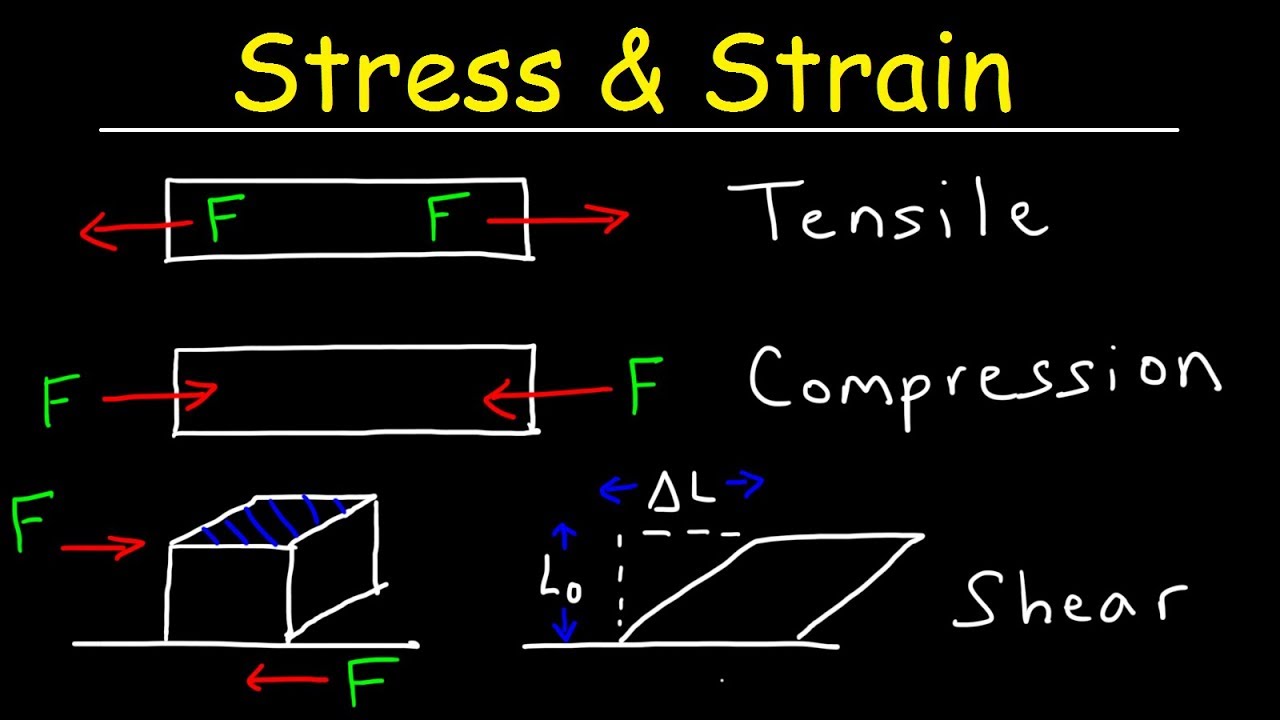
• 📉 Normal stress, which acts perpendicular to the material's surface, can be tensile (stretching) or compressive (shortening).
• 🔄 Stress and strain are closely related, and their relationship can be depicted through a stress-strain diagram, which varies with material type.
• 📈 Hooke's law describes the linear relationship between stress and strain for small deformations, defined by Young's modulus.
• 🔄 Shear stress, denoted by the Greek letter tau, is the internal force that acts parallel to the material's cross-section and is common in applications like bolts.
• 🔗 Both normal and shear stresses can be present at a point within a material, and their magnitudes depend on the observation plane's angle.
• 📚 Understanding stress and strain is foundational for more advanced topics in mechanics, such as torsion and beam bending.

Q & A

What are stress and strain, and how do they relate to the response of a body to external loads?

Stress and strain are fundamental concepts used to describe how a body responds to external loads. Stress is a measure of the internal force per unit area that develops within a body to resist applied forces, while strain is a measure of the deformation that occurs within the body as a result of these forces.

What is uniaxial loading, and how does it affect the stress distribution in a bar?

Uniaxial loading refers to a condition where all applied loads act along the same axis. In the case of a solid metal bar, uniaxial loading causes the bar to stretch, leading to the development of internal forces that resist the applied forces. The stress distribution in such a bar is uniform and perpendicular to the direction of the applied force.

How is stress defined and what are its units in SI and US units?

Stress is defined as the internal force per unit area. In SI units, it is measured in Newtons per meter squared, which is also known as Pascals. In US customary units, stress is measured in pounds per square inch.

What is normal stress, and how is it calculated for an axially loaded bar?

Normal stress is the type of stress that acts perpendicular to the cross-section of a body. For an axially loaded bar, normal stress is calculated as the applied force (F) divided by the cross-sectional area (A) of the bar. It is denoted by the Greek letter sigma (σ).

Why is it important to calculate stress, and how does it relate to material failure?

Calculating stress is important because it allows us to predict when an object will fail under applied loads. When the stress within a material exceeds its strength, the material will fail. For example, a bar made from mild steel with a strength of 250 MPa will fail if the applied force exceeds a certain threshold calculated based on its cross-sectional area.

What is the difference between tensile and compressive stress?

Tensile stress occurs when forces act to stretch or elongate a material, while compressive stress occurs when forces act to shorten or compress a material. Tensile stresses are considered positive, and compressive stresses are considered negative according to the conventional sign convention.

How is strain calculated, and what does it represent?

Strain is calculated as the change in length (ΔL) of a body divided by its original length (L). It represents the deformation that occurs within a body due to the application of force. Strain is a non-dimensional quantity and is often expressed as a percentage.

What is Hooke's law, and how does it relate to stress and strain?

Hooke's law states that within the elastic limit, the relationship between stress and strain is linear. This linear relationship is defined by Young's modulus, which is the ratio of stress to strain. Hooke's law typically applies for small strains, and deformations in this region are reversible when the load is removed.

What is shear stress, and how does it differ from normal stress?

Shear stress is the type of stress that acts parallel to the cross-section of a body, as opposed to normal stress which acts perpendicular. It is caused by forces that tend to slide one part of the material over another. Shear stress is denoted by the Greek letter tau (τ) and is calculated as the applied force (F) divided by the cross-sectional area (A).

How is shear strain defined, and how does it relate to the deformation of a body?

Shear strain is defined as the change in angle between two originally perpendicular lines within a body due to shear stress. It represents the deformation that occurs in the shape of the body without changing its volume. Shear strain is denoted by the Greek letter gamma (γ).

What is a stress element, and why is it used in stress analysis?

A stress element is a graphical representation used to depict the normal and shear stresses acting at a single point within a body. It is used in stress analysis to visualize and understand the complex stress state at a point, which can have components in both normal and shear directions depending on the orientation of the plane used to observe the stresses.