Generalized Hooke’s Law — Lesson 3

Summary

This video explores the extension of Hooke’s law from one-dimensional to three-dimensional applications, illustrating how materials behave under various stress states. Using examples like a belt drive, satellite structure, and submarine, it explains the impact of uniaxial and biaxial stresses, along with Poisson’s effect. The discussion includes the importance of shear strains and introduces compliance and stiffness tensors, emphasizing the linear relationship between stress and strain. It also highlights non-isotropic materials, particularly fibrous structures, that exhibit unique stiffness properties due to fiber orientation, providing a comprehensive overview of material mechanics.

Takeaways

• 😀 Hooke's law extends from one-dimensional to three-dimensional cases, requiring careful consideration of various stress and strain components.
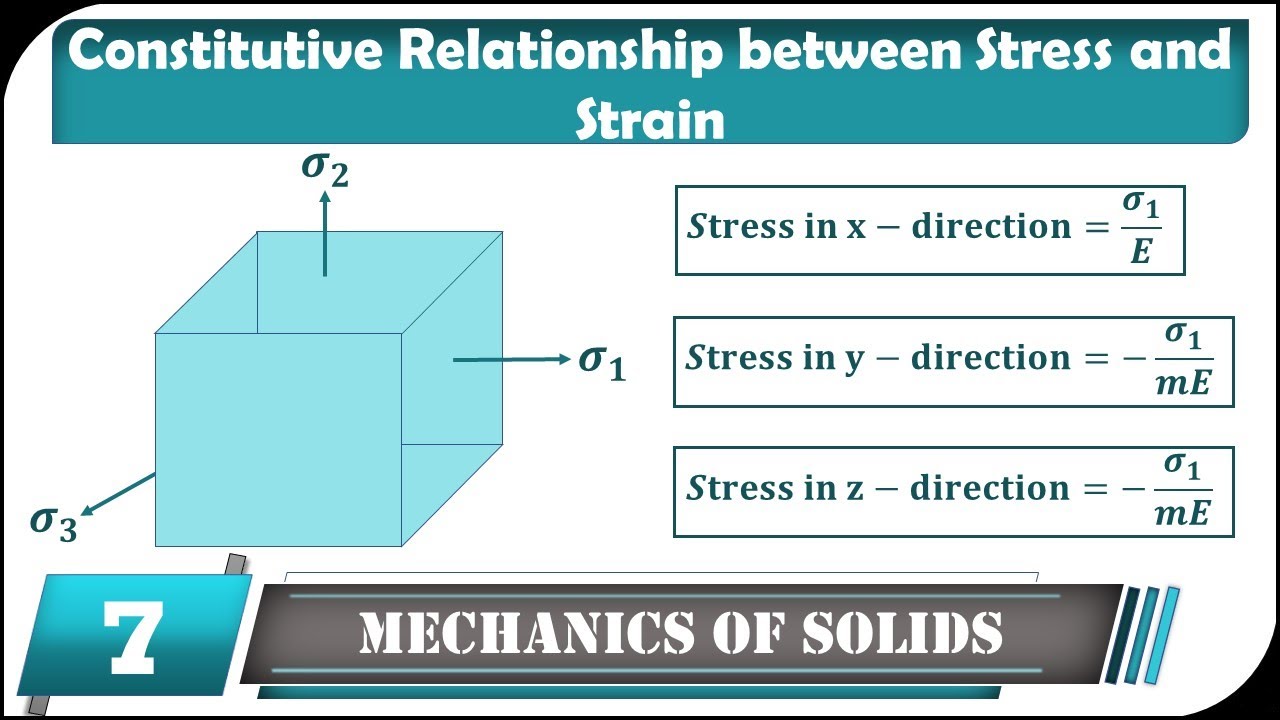
• 😀 In uniaxial stress scenarios, strain is determined by the formula: strain = sigma_XX/E, where sigma_XX is the stress in the x-direction.
• 😀 Poisson's effect explains how materials deform in perpendicular directions, with strains in the y and z directions represented as -nu*sigma_XX/E.
• 😀 The example of a satellite shows how biaxial stress states arise when forces act in two perpendicular directions, influencing both normal strains.
• 😀 In submarines, normal stresses in all three directions due to buoyant forces illustrate the need to account for volumetric strain in calculations.
• 😀 Shear strains in materials are crucial, and it is important to distinguish between engineering shear strain and true shear strain in applications.
• 😀 Brake pad assemblies highlight the complexity of strain tensors, which include both normal and shear stresses during operation.
• 😀 The compliance tensor relates stress to strain in a linear format, while its inverse, the stiffness matrix, defines the material's response to stress.
• 😀 The discussion emphasizes the concept of isotropy, where materials are assumed to behave homogeneously, though many are actually anisotropic.
• 😀 Fibrous materials exemplify anisotropic behavior, showing greater stiffness along the direction of fiber orientation.

Q & A

What is Hooke's Law and how does it apply in three dimensions?

Hooke's Law states that the strain in a material is proportional to the applied stress, and this relationship extends to three dimensions by accounting for stresses and strains in multiple directions, including the effects of Poisson's ratio.

What is Poisson's effect?

Poisson's effect describes how materials deform in directions perpendicular to the direction of applied stress, resulting in contraction or expansion in those directions based on the material's Poisson's ratio.

How is the strain in the Y and Z directions calculated in a uniaxial stress state?

In a uniaxial stress state, the strains in the Y and Z directions are given by -nu * sigma_XX / E, where nu is Poisson's ratio, sigma_XX is the stress in the X direction, and E is Young's modulus.

What distinguishes a bi-axial stress state from uniaxial stress?

A bi-axial stress state involves applied stresses in two perpendicular directions, while a uniaxial stress state involves stress in only one direction, affecting the strain calculations accordingly.

What role does the bulk modulus play in material behavior?

The bulk modulus quantifies a material's resistance to uniform compression, and it relates volumetric strain to hydrostatic stress, indicating how materials respond to changes in volume.

How do shear strains differ from normal strains?

Shear strains occur due to forces that cause deformation parallel to the material's cross-section, while normal strains are due to forces acting perpendicular to the cross-section.

What is the significance of the compliance tensor in Hooke's Law?

The compliance tensor relates stress to strain in isotropic materials, allowing for a matrix representation of how materials deform under various stress conditions.

How does the stiffness matrix relate to the compliance tensor?

The stiffness matrix is the inverse of the compliance tensor, representing how stress relates to strain in a material and showing the material's ability to resist deformation.

What is the difference between engineering shear strain and true shear strain?

Engineering shear strain is defined as the total change in angle (including a factor of 2 for symmetry), while true shear strain reflects the actual angular change without this factor.

Why are many materials considered anisotropic?

Many materials are anisotropic because their structural characteristics, such as fiber orientation, lead to different stiffness and behavior in different directions, unlike isotropic materials that exhibit uniform properties.