RC Low Pass Filter Explained

Summary

This video from the 'All About Electronics' YouTube channel delves into the fundamentals of passive electronics filters, specifically focusing on low-pass filters. It explains the concept of filters that allow low-frequency signals while attenuating higher ones. The script covers the types of filters, including low-pass, high-pass, band-pass, and band-reject, and emphasizes the distinction between active and passive filters. It then provides an in-depth look at the first-order RC low-pass filter, detailing its design, frequency response, and phase shift characteristics. The video also illustrates how to calculate the -3dB frequency and output voltage for a given input signal, offering practical insights into filter design and its applications.

Takeaways

• 🔧 Passive electronic filters are circuits that pass certain frequency components while rejecting or attenuating others.
• ⚙️ Filters are classified into four types: Low Pass Filter, High Pass Filter, Band-Pass Filter, and Band-Reject Filter.
• 📉 A Low Pass Filter passes signals from 0 Hz up to a cutoff frequency and attenuates higher frequencies.
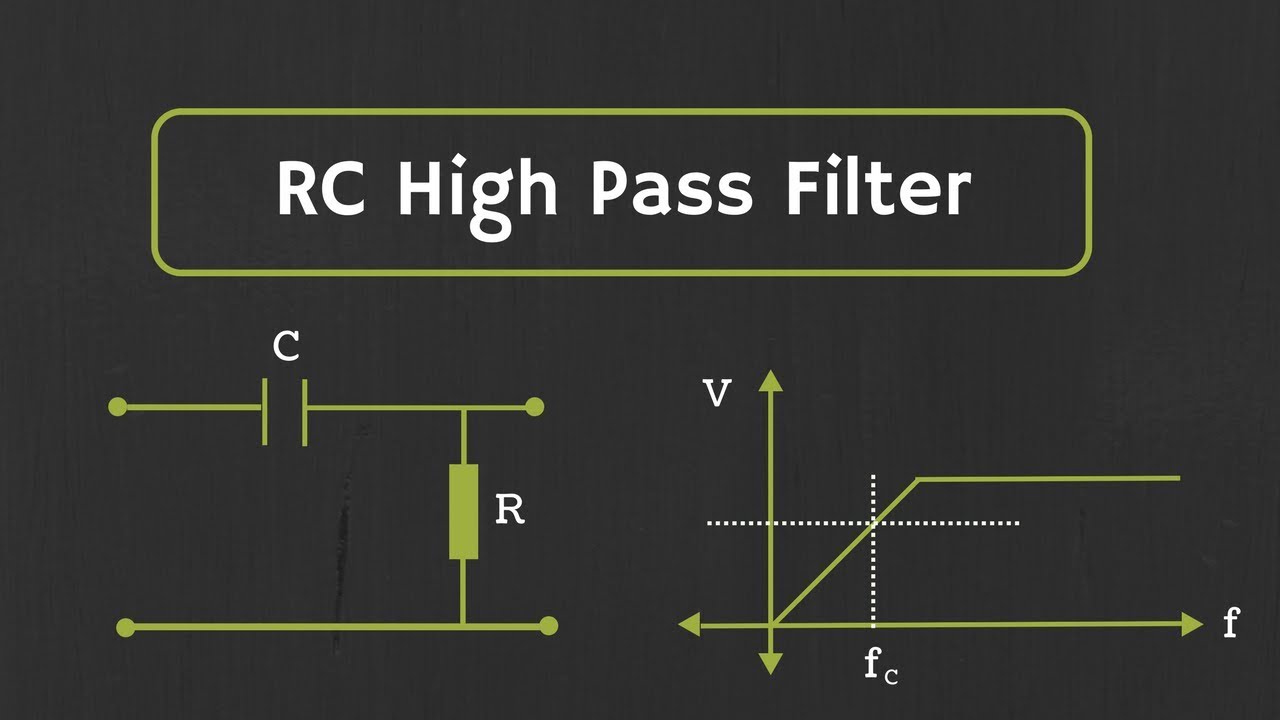
• 📈 A High Pass Filter allows signals above a cutoff frequency to pass, while attenuating lower frequencies.
• 🔊 A Band-Pass Filter passes frequencies within a specific range and rejects those outside of it.
• 🔇 A Band-Reject Filter does the opposite, rejecting frequencies within a specific range and passing others.
• 📏 The cutoff frequency for a first-order RC low pass filter is determined by the formula 1/(2πRC).
• 🔬 Active filters use active components like Op-Amps and transistors, providing gain, whereas passive filters use resistors, capacitors, and inductors, and output less than the input.
• 📉 The output of a low-pass filter decreases as frequency increases, with the output at the cutoff frequency being 0.707 times the input.
• 🎚️ Higher-order filters provide sharper roll-off, with attenuation increasing by 20 dB/decade for each order.

Q & A

What is an electronic filter and what does it do?

An electronic filter is a circuit that allows certain frequency components to pass through while rejecting or attenuating all other frequency components. It processes the input signal by filtering out unwanted frequencies.

How many types of filters are mentioned in the script, and what are they?

Four types of filters are mentioned: Low Pass Filter, High Pass Filter, Band Pass Filter, and Band Reject Filter. Each type is designed to pass or reject specific frequency bands.

What is the primary difference between an active filter and a passive filter?

Active filters are designed using components like Op-Amp and transistors, which can provide gain to the input signal. Passive filters, on the other hand, are designed using components like resistors, capacitors, and inductors, and the output is always less than the input.

What is the formula for calculating the cut-off frequency of a first-order low-pass filter?

The cut-off frequency (fc) of a first-order low-pass filter is given by the formula fc = 1/(2πRC), where R is the resistance and C is the capacitance in the filter circuit.

What is the significance of the -3dB frequency in the context of filters?

The -3dB frequency, also known as the cut-off frequency, is the frequency at which the output is 0.707 times the input, indicating a 3dB reduction in amplitude. It is a key parameter in determining the filter's performance.

How does the phase of the output signal change as the input frequency increases in a low-pass filter?

In a low-pass filter, as the input frequency increases, the phase of the output signal lags behind the input signal. At the cut-off frequency, the phase lag is -45 degrees, and it approaches -90 degrees at very high frequencies.

What is the output voltage of a 10 V, 2 kHz sinusoidal input signal applied to the given low-pass filter in the script?

The output voltage for a 10 V, 2 kHz sinusoidal input signal applied to the given low-pass filter is 6.22 V, as calculated using the formula for output voltage in the script.

How does the attenuation rate change with the order of the filter?

The attenuation rate increases with the order of the filter. For an nth order filter, the roll-off rate is -20*n dB/decade, meaning higher order filters provide a sharper roll-off and greater attenuation at higher frequencies.

What is the purpose of cascading first-order low-pass filters to create a higher order filter?

Cascading first-order low-pass filters increases the overall order of the filter, which results in a sharper roll-off and greater attenuation at higher frequencies, thus improving the filter's performance.

Why is it important to consider loading effects when designing higher order filters by cascading first-order filters?

Loading effects occur when the input impedance of the second stage affects the output impedance of the first stage, potentially degrading the filter performance. To minimize this, the value of R2 should be at least 10 times R1, or active filters can be used to provide buffering between stages.