Komposisi Fungsi Part 2 - Operasi Komposisi Fungsi dan Sifat-sifatnya [ Matematika Wajib Kelas X ]
Summary
TLDRIn this video, Deni and Handayani from Metland channel explore the concept of function composition, demonstrating how to combine two functions (G and F) to form a new function. They discuss the notation, properties, and provide examples, including calculating the composition of functions with given outputs and inputs. The video also introduces the properties of associative and identity functions in composition.
Takeaways
- 😀 The video is a continuation of a series on function composition, following the first part about algebraic operations on functions in Sumatra.
- 📚 Viewers are encouraged to watch the first video for foundational knowledge before proceeding with the second part on function composition.
- 🔁 The concept of function composition is introduced using an analogy of two machines processing wood into paper, emphasizing the sequential application of two functions.
- 🔄 Function composition is defined as the process of combining two or more functions in a specific order to create a new function.
- 📝 The notation for function composition is \( f(g(x)) \), which is read as 'f composed with g of x', highlighting the substitution of the inner function's output into the outer function.
- 📚 The script provides a step-by-step example of how to perform function composition, including substituting values into the functions and simplifying the result.
- 📘 The video includes multiple examples and exercises to illustrate the process of finding composite functions, such as \( f(g(x)) \) and \( g(f(x)) \), and their respective results.
- 🔢 The importance of understanding the domain and range of each function in the composition is highlighted, as it affects the validity of the composite function.
- 🎓 The script explains the non-commutative property of function composition, stating that \( g(f(x)) \) is not necessarily equal to \( f(g(x)) \).
- 🔗 It discusses the associative property, which states that the order in which functions are composed does not affect the final result when composed in a sequence, such as \( (f(g(x))) \) being equivalent to \( f(g(h(x))) \).
- 🆔 The identity function is introduced as a special case in function composition, where composing any function with the identity function results in the original function itself.
Q & A
What is the main topic of the video?
-The main topic of the video is the concept of function composition, including its operations, properties, and examples.
What is the analogy used in the video to explain function composition?
-The analogy used in the video is that of two machines processing wood into paper, where each machine represents a function and the process of passing the wood through both machines represents function composition.
What are the two functions, G and F, used in the video to demonstrate function composition?
-The functions G and F are represented as G(x) = x - 2 and F(x) = 2x + 1, respectively.
How is the result of the composition of functions G and F, denoted as F(G(x)), calculated in the video?
-The result of F(G(x)) is calculated by substituting G(x) into F(x), which in the given example results in 2(x - 2) + 1, simplifying to 2x - 3.
What is the notation used for function composition in the video?
-The notation used for function composition in the video is 'F ∘ G(x)', read as 'F composed with G of x'.
What is an example of a property of function composition mentioned in the video?
-One of the properties mentioned in the video is that function composition is not commutative, meaning that G ∘ F is not necessarily equal to F ∘ G.
What is the identity function in the context of function composition as discussed in the video?
-The identity function, denoted as I(x) = x, is a function that when composed with another function, leaves the function unchanged. For example, F ∘ I or I ∘ F is equal to F.
How many examples of function composition are provided in the video?
-The video provides three examples of function composition, each with different functions and demonstrating the process of finding the composed function.
What is the purpose of the exercises given at the end of the video?
-The purpose of the exercises is to give the viewers practice in applying the concept of function composition and to test their understanding of the material covered in the video.
What additional topics related to function composition are mentioned as being covered in the next video?
-The next video will cover more complex problems involving function composition, including cases where the composition is known and the original functions need to be determined.
How can viewers access the solutions to the exercises provided in the video?
-The solutions to the exercises will be discussed in the next video, and the link to that video will be provided in the video description for viewers to access.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Verifying inverse functions by composition | Mathematics III | High School Math | Khan Academy

Komposisi Fungsi - Matematika Wajib Kelas XI Kurikulum Merdeka

Composite Function | General Mathematics @MathTeacherGon

Composition of Function by Ma'am Ella Barrun
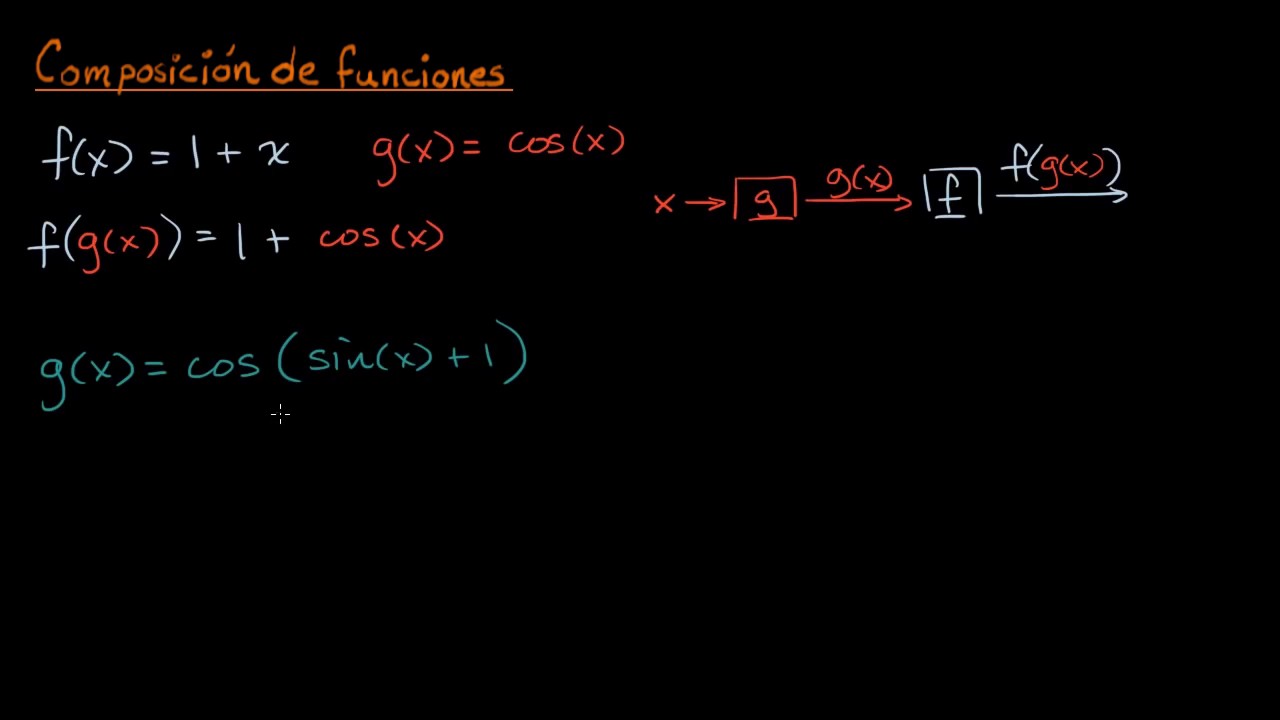
Reconocer una composición de funciones | Khan Academy en Español

FUNGSI KOMPOSISI dengan 3 fungsi
5.0 / 5 (0 votes)
