Average vs Instantaneous Rates of Change
Summary
TLDRThis video script explains the difference between average and instantaneous rates of change in calculus. The average rate of change is the slope between two points, calculated as (f(B) - f(A)) / (B - A), equivalent to the slope formula from algebra. Instantaneous rate of change is the derivative at a specific point, representing the slope of the tangent line. An example using the function x^2 + x + 1 illustrates the calculation of both rates, with the average rate of change between 0 and 1 being 2, and the instantaneous rate of change at x=1 being 3.
Takeaways
- 📐 The average rate of change is calculated as \( \frac{f(B) - f(A)}{B - A} \), which is the slope between two points on a function.
- 🔍 This formula is similar to \( \frac{y_2 - y_1}{x_2 - x_1} \) from algebra, representing the slope of a line.
- 📉 The average rate of change can also be referred to as the slope of a secant line between two points on a curve.
- 📈 The instantaneous rate of change is the rate of change at a specific point, which is found using the derivative of the function at that point.
- 🧭 Instantaneous rate of change is the slope of the tangent line to the curve at a particular point.
- 🔢 For the function \( x^2 + x + 1 \), the average rate of change between \( x = 0 \) and \( x = 1 \) is 2, indicating a steeper increase than a constant rate.
- 📌 To find the average rate of change, substitute the interval endpoints into the function and calculate the difference quotient.
- 💡 The instantaneous rate of change at \( x = 1 \) for the same function is found by evaluating the derivative at that point, yielding a value of 3.
- ✏️ The derivative of \( x^2 + x + 1 \) is \( 2x + 1 \), which can be calculated using the power rule for derivatives.
- 🎯 The distinction between average and instantaneous rates of change is crucial for understanding how functions behave over intervals versus at specific points.
Q & A
What is the average rate of change in calculus?
-The average rate of change in calculus is the ratio of the change in the function's output (f(B) - f(A)) to the change in the input (B - A) over an interval, which can also be thought of as the slope between two points or the slope of a secant line.
How is the average rate of change formula related to the slope formula from algebra?
-The average rate of change formula is essentially the same as the slope formula from algebra, which is (y2 - y1) / (x2 - x1), representing the slope between two points.
What is the instantaneous rate of change?
-The instantaneous rate of change is the rate of change at a single point, which is represented by the derivative of the function at that point, or the slope of the tangent line at that point.
What is the main difference between average and instantaneous rates of change?
-The main difference is that the average rate of change is the slope between two points, while the instantaneous rate of change is the slope at a single point, represented by the function's derivative at that point.
What function was used in the example to explain average and instantaneous rates of change?
-The function used in the example was f(x) = x^2 + x + 1.
How do you calculate the average rate of change for the function f(x) = x^2 + x + 1 on the interval [0, 1]?
-You calculate it by finding f(1) = 1^2 + 1 + 1 = 3 and f(0) = 0^2 + 0 + 1 = 1, then the average rate of change is (f(1) - f(0)) / (1 - 0) = (3 - 1) / (1 - 0) = 2.
What is the instantaneous rate of change at x = 1 for the function f(x) = x^2 + x + 1?
-The instantaneous rate of change at x = 1 is found by taking the derivative of the function, which is f'(x) = 2x + 1, and then evaluating it at x = 1, giving f'(1) = 2*1 + 1 = 3.
What is the derivative of the function f(x) = x^2 + x + 1?
-The derivative of the function f(x) = x^2 + x + 1 is f'(x) = 2x + 1, which can be found using the power rule for differentiation.
How does the concept of a secant line relate to the average rate of change?
-The average rate of change is the slope of the secant line, which connects two points on a curve, indicating how the function changes over that interval.
How does the concept of a tangent line relate to the instantaneous rate of change?
-The instantaneous rate of change is the slope of the tangent line at a specific point on the curve, indicating the rate of change of the function at that exact point.
What is the significance of understanding the difference between average and instantaneous rates of change?
-Understanding the difference is crucial for grasping the concepts of derivatives and rates of change in calculus, which are fundamental to analyzing functions and their behavior.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
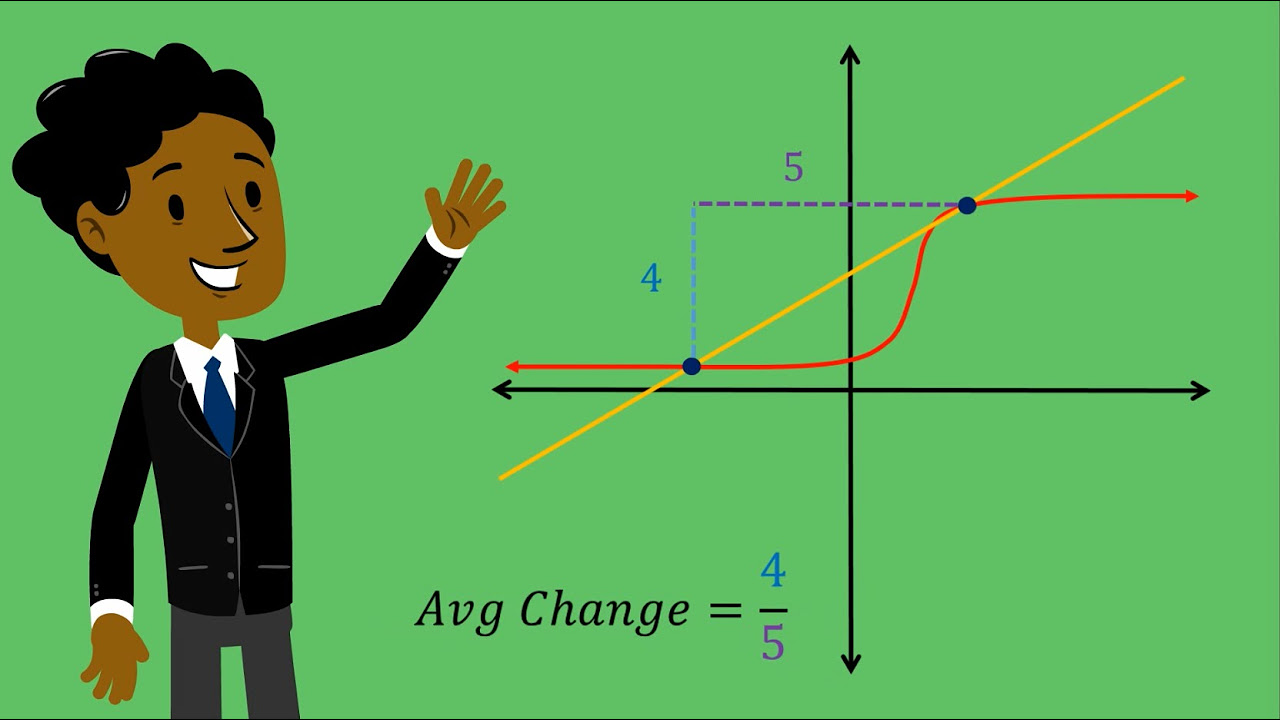
Calculus - Average Rate of Change of a Function

Calculus Made EASY! Learning Calculus
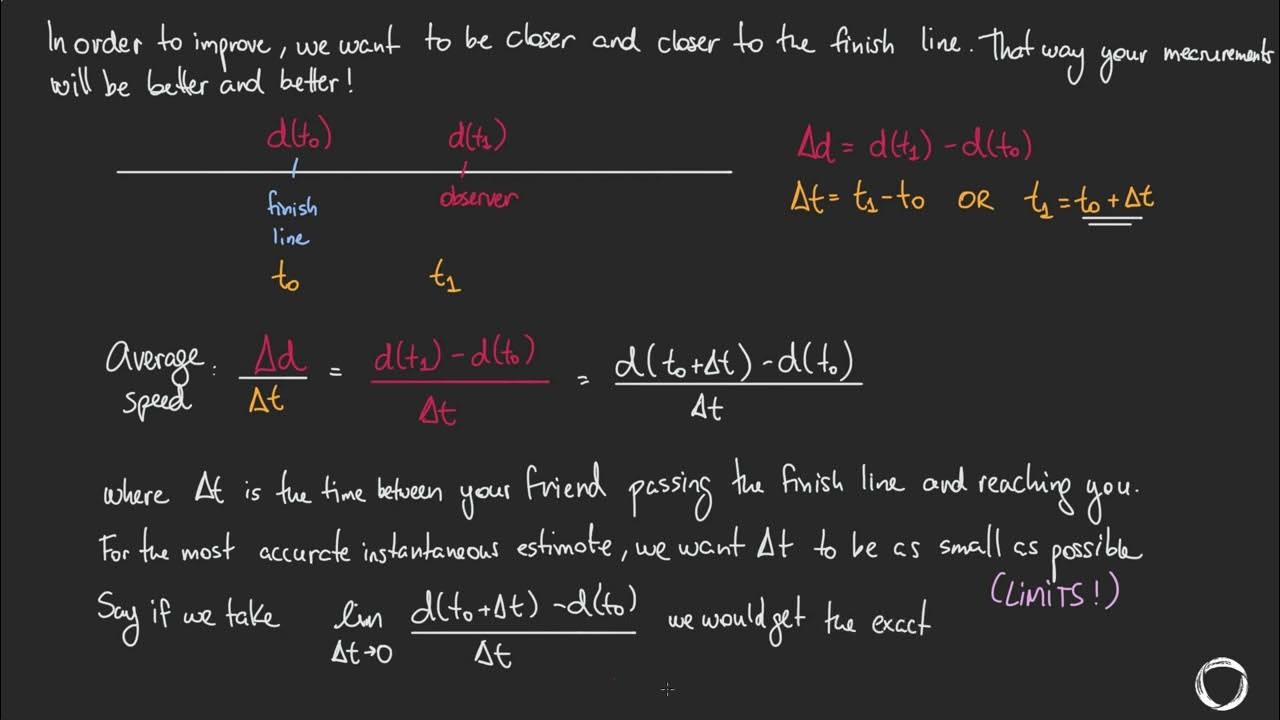
Average and Instantaneous Rates
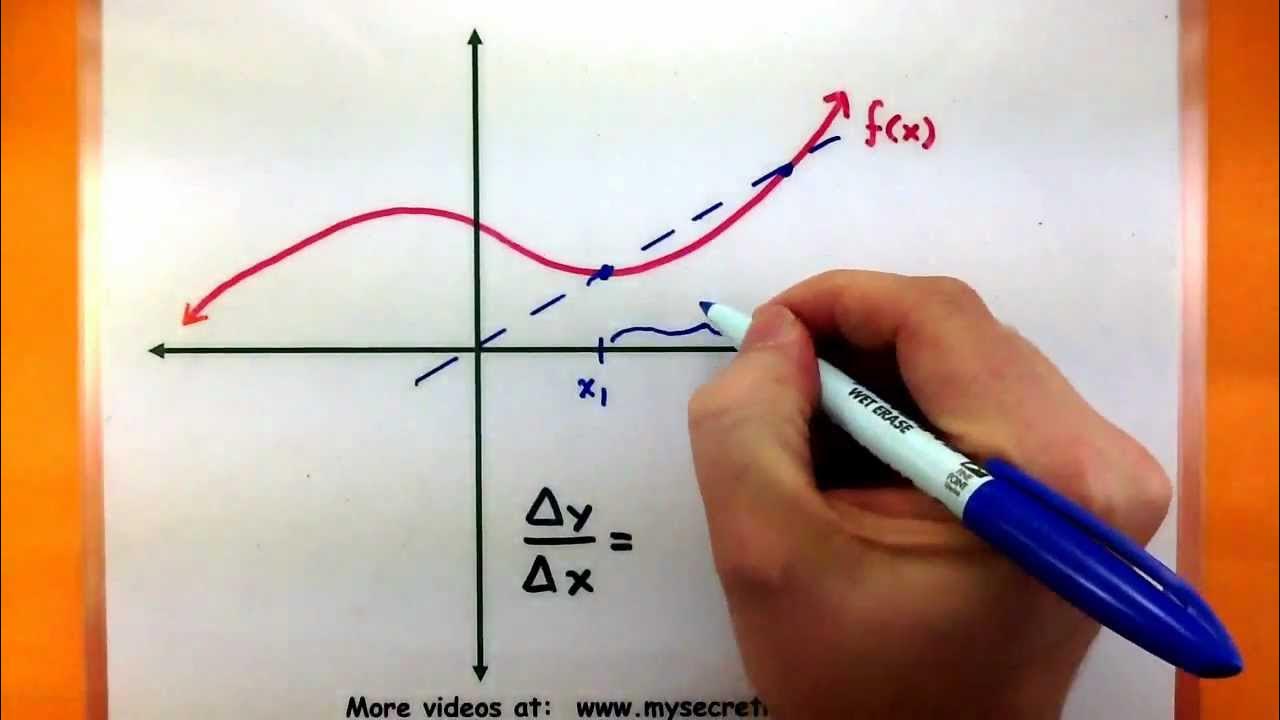
Calculus - Average rate of change of a function

What is Calculus in Math? Simple Explanation with Examples

Instantaneous speed and velocity | One-dimensional motion | Physics | Khan Academy
5.0 / 5 (0 votes)
