Calculus - Average rate of change of a function

Summary

This video script delves into the concept of the average rate of change of a function, a fundamental topic in calculus. It explains two methods to calculate this rate: one that requires knowing the exact coordinates of two points on the function, and another, the difference quotient, which simplifies the process by using a single point and the distance from it. The script emphasizes the practicality of the difference quotient for computing average rates of change, especially when dealing with limits, and promises further examples in upcoming videos.

Takeaways

• 📚 The average rate of change of a function is a measure of how much the output (y-values) changes relative to the input (x-values) between two points.
• 📈 There are multiple methods to calculate the average rate of change, but the script focuses on two primary approaches: graphical and analytical.
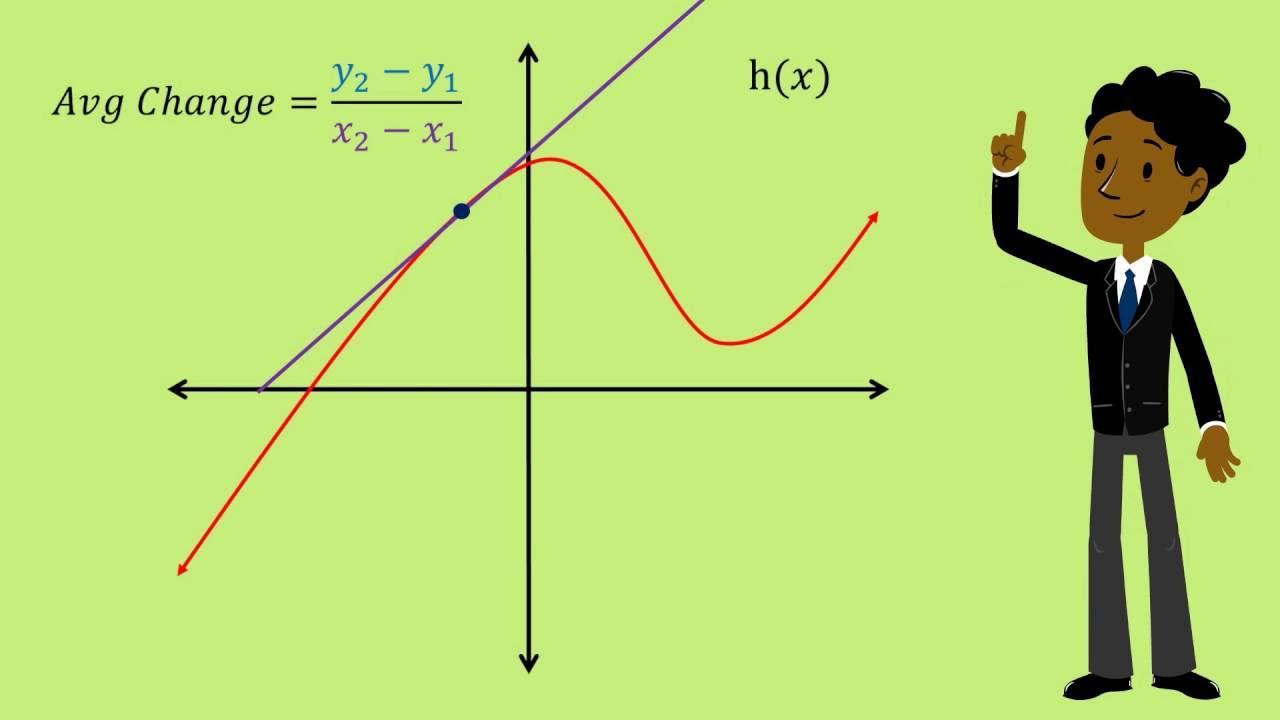
• 🔍 The graphical approach involves drawing a secant line between two points on the graph of a function and calculating its slope.
• 📍 To find the slope of the secant line, one must identify the x and y values of two points, labeled as (X1, f(X1)) and (X2, f(X2)).
• 🧭 The formula for the slope of the secant line is given by (f(X2) - f(X1)) / (X2 - X1), which represents the average rate of change between the two points.
• 🔄 An alternative analytical method defines the second point in terms of a distance 'h' from the first point, with coordinates (X1 + h, f(X1 + h)).
• 📝 The difference quotient is introduced as a formula to compute the average rate of change using the first point and a distance h: (f(X1 + h) - f(X1)) / h.
• 🔑 The difference quotient is advantageous because it only requires knowledge of one point and the distance to the second point, simplifying calculations as the second point moves.
• 📉 As the distance 'h' approaches zero, the difference quotient can be used to find the instantaneous rate of change, which is foundational in understanding limits in calculus.
• 👨‍🏫 The script suggests that understanding the difference quotient is crucial for deeper study in calculus, particularly when exploring limits and derivatives.
• 🔍 The video script also implies that the difference quotient will be used in further videos to demonstrate how to find the average rate of change for various functions.

Q & A

What is the average rate of change of a function?

The average rate of change of a function is a measure of how much the y-values of the function change relative to the change in the x-values between two specific points on the function.

How is the average rate of change of a function typically found?

The average rate of change is found by calculating the slope of the secant line that passes through two points on the function, which is the difference in y-values divided by the difference in x-values.

What are the two methods mentioned in the script for calculating the average rate of change?

The two methods mentioned are calculating the slope of the secant line using the coordinates of two points and using the difference quotient, which involves a single point and a distance from that point.

Why is the difference quotient considered a better starting point for computing the average rate of change?

The difference quotient is considered better because it only requires knowledge of a single point and a distance from that point, making it easier to work with as the second point's location changes.

What is the formula for the difference quotient?

The difference quotient formula is (f(X1 + H) - f(X1)) / H, where X1 is the x-value of the fixed point and H is the distance from that point.

How does the script suggest defining the second point in the difference quotient method?

The script suggests defining the second point in terms of a distance H away from the first point, with an x-value of X1 + H.

What is the significance of the secant line in the context of the average rate of change?

The secant line represents the average rate of change between two points on the function, as its slope is the measure of how the function changes over the interval between those points.

How does the script illustrate the process of finding the average rate of change graphically?

The script uses a graphical representation of a function with two points marked by blue dots, and it shows the secant line between these points to visually represent the average rate of change.

What is the main advantage of using the difference quotient over the direct method of using two points?

The main advantage is that the difference quotient simplifies the process when one point is fixed and the other point's location is varied, as it only requires the distance from the fixed point rather than exact coordinates.

Why might knowing the exact coordinates of the second point become impractical in certain situations?

Knowing the exact coordinates becomes impractical when one point is fixed and the other point's location is continuously varied, as it becomes increasingly difficult to determine the x and y values for the moving point.

How does the script relate the concept of the average rate of change to the study of limits in calculus?

The script hints that the difference quotient is foundational to understanding limits, suggesting that as the distance H approaches zero, the difference quotient can be used to find the instantaneous rate of change, which is related to derivatives and limits.

Outlines

00:00

📊 Understanding Average Rate of Change

This paragraph introduces the concept of the average rate of change of a function, a fundamental topic in calculus. The speaker explains that it involves examining how the y-values of a function change in relation to the x-values between two specific points. Two methods for calculating this rate are mentioned: graphically and algebraically. The graphical approach involves finding the slope of the secant line between two points on the function, identified by their x-values (X1 and X2) and corresponding y-values (f(X1) and f(X2)). The algebraic method is demonstrated through the formula for the average rate of change, which is the difference in y-values divided by the difference in x-values, simplified as (f(X2) - f(X1)) / (X2 - X1). The paragraph emphasizes the importance of understanding this concept for further study in calculus.

05:02

🔍 Exploring the Difference Quotient

The second paragraph delves deeper into the algebraic approach to finding the average rate of change, focusing on the difference quotient. The speaker describes an alternative way to define the second point on the function, not by its specific x-value, but by its distance 'H' from the first point X1, making the second point X1 + H. The difference quotient formula is introduced as a simplified method to calculate the slope of the secant line, expressed as (f(X1 + H) - f(X1)) / H. This method is highlighted as more practical when dealing with limits and as the foundation for understanding instantaneous rates of change. The paragraph concludes by encouraging viewers to become familiar with the difference quotient for more advanced calculus topics, promising further examples in upcoming videos.

Keywords

💡Average Rate of Change

The average rate of change is a fundamental concept in calculus that describes the rate at which the output of a function changes with respect to its input over a certain interval. In the video, it is used to understand how much the y-values of a function change relative to the change in its x-values between two points. The script explains that this can be graphically represented by the slope of the secant line between two points on the graph of the function.

💡Function

A function in mathematics is a relation between a set of inputs and a set of permissible outputs, with the property that each input is related to exactly one output. In the context of the video, the function is denoted as 'f(x)', and the discussion revolves around how the function changes over a given interval, which is essential for calculating the average rate of change.

💡Secant Line

A secant line is a straight line that intersects a curve at two or more points. In the video, the secant line is used to represent the average rate of change of the function between two specific points. The slope of this secant line is calculated to find the average rate at which the function changes over the interval defined by these points.

💡Slope

Slope is a measure of the steepness of a line, typically represented as the ratio of the change in the y-coordinate to the change in the x-coordinate between two points on the line. In the video, the slope of the secant line is used to determine the average rate of change of the function, which is calculated by subtracting the y-values and dividing by the difference in the x-values of the two points.

💡X and Y Values

In the context of the video, x and y values refer to the coordinates of points on the graph of a function. The x-value represents the input to the function, while the y-value represents the output or the value of the function at that input. The script discusses how these values are used to calculate the average rate of change by plugging the x-values into the function to find the corresponding y-values.

💡Difference Quotient

The difference quotient is a formula used to find the slope of the secant line between two points on a graph, which is equivalent to the average rate of change of the function. In the video, it is introduced as an alternative method to calculate the average rate of change, where one point is fixed, and the other is defined in terms of a distance from the first point, simplifying the calculation process.

💡Limits

In calculus, limits are a fundamental concept that describes the value that a function or sequence 'approaches' as the input or index approaches some value. The video hints at the deeper application of the difference quotient in the context of limits, where as the distance 'h' between the two points becomes infinitesimally small, the difference quotient can be used to find the instantaneous rate of change.

💡Graphical Representation

Graphical representation in the video refers to the visual depiction of the function and the secant line on a graph. This visual aid is crucial for understanding the concept of the average rate of change by showing the slope of the line between two points, which is a direct way to see how the function changes over an interval.

💡Instantaneous Rate of Change

While not explicitly defined in the script, the concept is alluded to as the video discusses the difference quotient and its relation to limits. The instantaneous rate of change is the derivative of a function at a specific point, which can be thought of as the average rate of change as the interval between points becomes infinitely small.

💡Distance 'H'

In the script, 'H' represents the distance from the first point on the function to the second point. This is used in the alternative method of calculating the average rate of change, where the second point's x-value is expressed as 'X1 + H'. This approach simplifies the calculation by allowing the use of a single point and a distance, rather than needing the exact x and y values of two points.

Highlights

Introduction to the concept of average rate of change of a function in calculus.

Explanation of how the average rate of change is calculated by comparing changes in y-values to changes in x-values.

Introduction of two methods to approach the problem of finding the average rate of change.

Graphical representation of the secant line between two points on a function to find its slope.

Identification of the need for x and y values of two points to compute the average rate of change.

Presentation of the formula for calculating the average rate of change between two points.

Discussion of the limitations of the first method when points are not precisely known.

Introduction of an alternative method using a fixed point and a variable distance to define the second point.

Explanation of defining the second point as a distance H away from the first point.

Use of the difference quotient to compute the average rate of change with a single point and a distance.

Simplification of the formula using the difference quotient for easier computation.

Advantages of using the difference quotient for calculating the average rate of change as it requires less specific point data.

The importance of the difference quotient in understanding limits and deeper calculus concepts.

Promise of further videos to provide examples of using the difference quotient.

Emphasis on the practicality of the difference quotient for easier manipulation as the distance becomes smaller.

Transcripts

I'm going to talk about the average rate

of change of a function so you may have

heard your Calculus teacher talk about

this topic and wondered what exactly are

they talking about well when finding the

average rate of change of a function

you're basically looking at how much the

yv values of that function change versus

how much the X values change between two

particular points on that function now

there's actually a couple of ways that

you could approach this type of problem

and so I'm going to show you both ways

graphically and kind of the ideas of why

we're going to use one over the other

all right so go ahead and let's check

this

out suppose we have a function and let's

call it f ofx I'm curious about how much

this function changes between two

particular points and I'll go ahead and

mark them out uh with these two blue

dots like this in order to figure out

how much the function is changing

between those two points what I'll

essentially be doing is looking for the

slope of the secant line that goes

between them so if I had to draw that

secant line it would look something like

this there we are so we are curious as

the slope of that line now in order to

compute this I need to know where these

points are

located well this essentially amounts to

knowing their X and Y values so for sake

of argument I will label this guy

X1 and I will label the x value of this

one as

X2 to figure out their y values I would

essentially take this x value and plug

it into the

function so to keep things nice and

general I'll say that its x value is X1

and it's y value I find that when I plug

in X1 into the function so this point is

located at at X1 F of X1 and this point

is located at

X2 F of

X2 all right now to compute the slope

basically I'm looking at subtracting the

Y values divided by subtracting the X

values so I have F of

X2 minus F of

X1 all

over X2 -

X1 so this formula right here will give

me the average r change for this

particular function between these two

points X1 and X2 now this isn't the only

way to compute it nor is this

necessarily the way we want to start

Computing average rates of change

between two points the reason is when we

go this direction we essentially have to

know exactly where these two points are

we need both of their X values and we

need both of their y values the reason

why that you know that's not going to be

very handy in the future is we'll

essentially fix one of these points and

start moving where the the other one is

and if we start moving that other point

it's going to get harder and harder to

determine where those X and Y values for

the second Point always end

up so instead let's look at the same

problem from a different angle and see

another way that we can compute the

average rate of

change so I'm essentially going to use

that same function that I did before F

ofx and I'm going to Define my points in

a slightly different

way let's go ahead and first put them on

our

graph

and again I'll be curious as to finding

that secant

line all right so like before I'm going

to call this first point its x value X1

and that's the one I'm really interested

in as for my second point I'm going to

Define this in a very interesting way

I'm going to Define it in terms of a

distance from my first point so this

second point is a distance of H

away now since it is a distance of H

away I can describe its x value as X1

plus this distance

H now that seems like a really funny way

to define the second point but just

follow me for a bit and you'll see why

it is important all right now in order

to do the average rate of change I need

some y values well Define that first

point exactly the same way as we did

before so

X1 and I basically plug it into the

function f of

X1 and I do the same thing with the

second point so it has an x value at X1

+ H and I could take that value and plug

it into the

function and get F of X1 +

H there you go so essentially I'm

defining the X and Y values in terms of

the first point and a distance from that

that first point now let's go ahead and

compute the slope of our secant line and

see the formula that this

builds so like before I'm going to

subtract my y

values so I take my second yalue F of X1

+ H I subtract the first y

value F of

X1 divid

[Music]

by subtract the X

values so x + 1

minus

X1 so you can see this this looks like

what we did before only I'm just using

X1 and H to do it now I can simplify

this formula just a little bit by

canceling out some extra x1's in the

bottom F of X1 + H

minus F of

X1 all over

H now this gives us what is known as the

difference quotient and it essentially

does the same thing as before it figures

out the slope of the secant line between

the two points now this is how you're

going to want to start Computing the

average rate of change between two

points because it's essentially doing it

only using a single point and a distance

the reason why that is so important is

again we'll basically fix one of our

points X1 we'll make sure it doesn't

move and we'll end up changing in where

the other one is using this new formula

I don't necessarily need to know where

that other one is instead I'll just need

to know how far away it is so when I

start making this distance smaller and

smaller and smaller I'll have an easier

time working with this difference

quotient than I will the uh first slope

formula so you definitely want to get

familiar familiar with this one and

you'll see it as we start building

deeper into

limits uh watch my further videos for

some examples on using the difference

quotient to find the average rate of

change for a

function