Calculus - Average Rate of Change of a Function
Summary
TLDRThis video script introduces the concept of function behavior in calculus, focusing on how functions increase and decrease. It uses the analogy of a roller coaster to visualize changes and contrasts the steepness of lines to represent different rates of increase. The script explains the importance of slope in describing a function's average rate of change between two points, and hints at the upcoming introduction of limits and instantaneous rates of change as key tools in calculus for a deeper understanding of function behavior.
Takeaways
- 📚 In Calculus, the focus is on understanding how functions change over their domain.
- 🎢 The function's behavior can be visualized as a roller coaster, indicating where it increases and decreases.
- 📈 The concept of a function's increase or decrease is intuitive but requires a precise measure for advanced analysis.
- 📊 Comparing the steepness of functions helps in understanding their rate of increase, which is not immediately intuitive.
- 📐 The notion of slope from linear equations is used to describe the rate of change in the y-direction relative to the x-direction.
- 🔍 The slope of a line can indicate whether one function increases more rapidly than another by comparing their slopes.
- 🤔 For non-linear functions, the idea of slope is adapted by drawing a line (tangent) between two points to approximate the function's change.
- 📉 The slope of such a line represents the average rate of change of the function between the two selected points.
- 🔄 Choosing different points on the function will yield different slopes, thus different average rates of change.
- 🚗 The average rate of change can have real-world applications, such as calculating average speed or flow rates.
- 🔮 The script introduces the concept of limits as a major tool in calculus for finding the instantaneous rate of change of a function at a single point.
Q & A
What is the main focus of the video script in terms of functions?
-The main focus is on understanding how functions change and the concept of their rates of increase or decrease.
How does the script suggest visualizing the changes in a function?
-The script suggests visualizing a function as a roller coaster to easily see where it increases and decreases.
What is the problem with just knowing if a function increases or decreases?
-While knowing if a function increases or decreases tells us about its behavior, it is not precise enough for detailed analysis and comparison of different functions.
How does the script compare the steepness of two increasing functions?
-The script compares the steepness by observing the slope of the lines representing the functions, with a steeper line indicating a more rapid increase.
What concept from working with lines is used to describe the rate of change of functions?
-The concept of slope is used to describe the rate of change of functions, by measuring the rise over the run between two points.
Why can't the idea of slope be directly applied to non-linear functions?
-The idea of slope cannot be directly applied to non-linear functions because they do not have a constant rate of change like lines do.
How can a line be used to approximate the change of a non-linear function?
-By choosing two points on the non-linear function and drawing a line through them, the slope of this line can be used as an approximation of the function's rate of change between those points.
What does the slope of a line between two points on a function represent?
-The slope of a line between two points on a function represents the average rate of change of the function between those points.
How does the script use the concept of slope to explain the average change of a function?
-The script uses the slope to explain that the average change of a function between two points is the ratio of the change in the y-direction to the change in the x-direction.
What is the next step after understanding the average rate of change?
-The next step is to learn how to describe how a function changes at a single point, which will involve the concept of limits and instantaneous rate of change.
What tool of calculus is mentioned as the first major tool to be introduced in the script?
-The first major tool of calculus mentioned is the limit, which will be used to describe the function's change at a single point.
Where can viewers find example problems about the average rate of change of a function?
-Viewers can find example problems about the average rate of change of a function on the provided website: MySecretMathTutor.com.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Übersicht f f´ f´´, Zusammenhänge der Funktionen/Graphen, Ableitungsgraphen | Mathe by Daniel Jung

Cálculo: Introdução e Noção Intuitiva de Limites (Aula 1 de 15)

Calculus - Introduction to Calculus
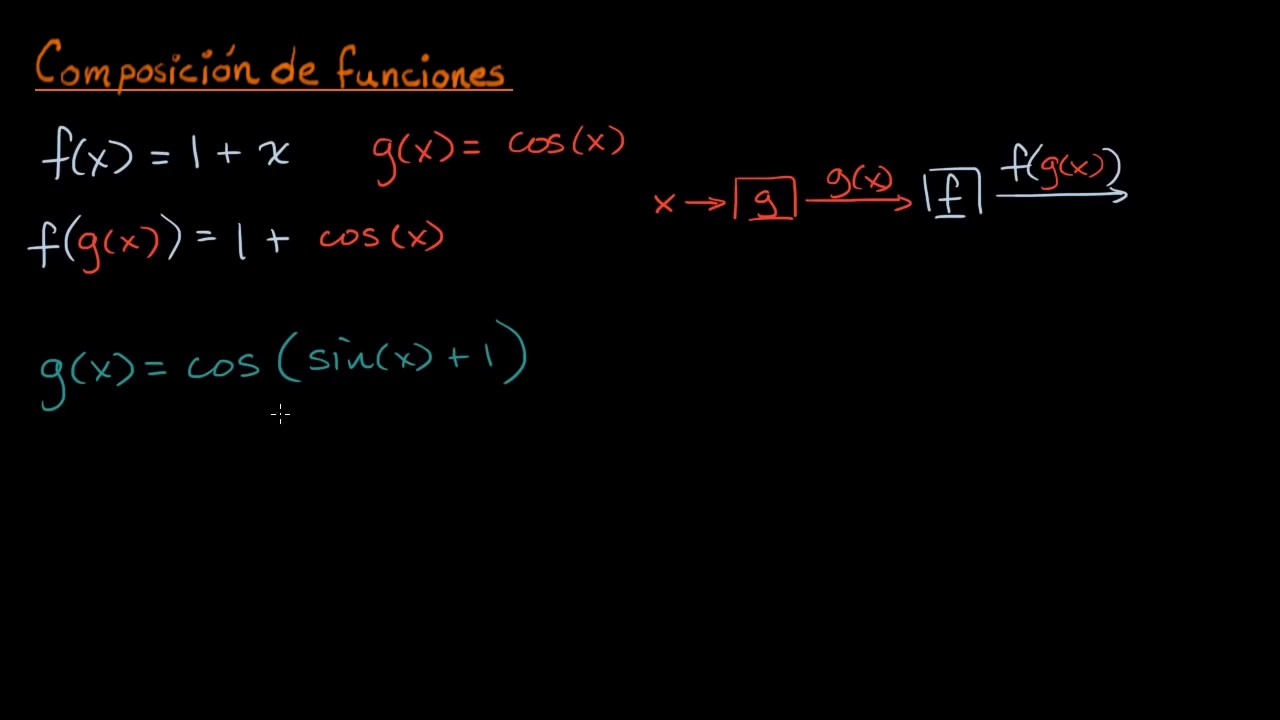
Reconocer una composición de funciones | Khan Academy en Español

Introduction to Complex Functions
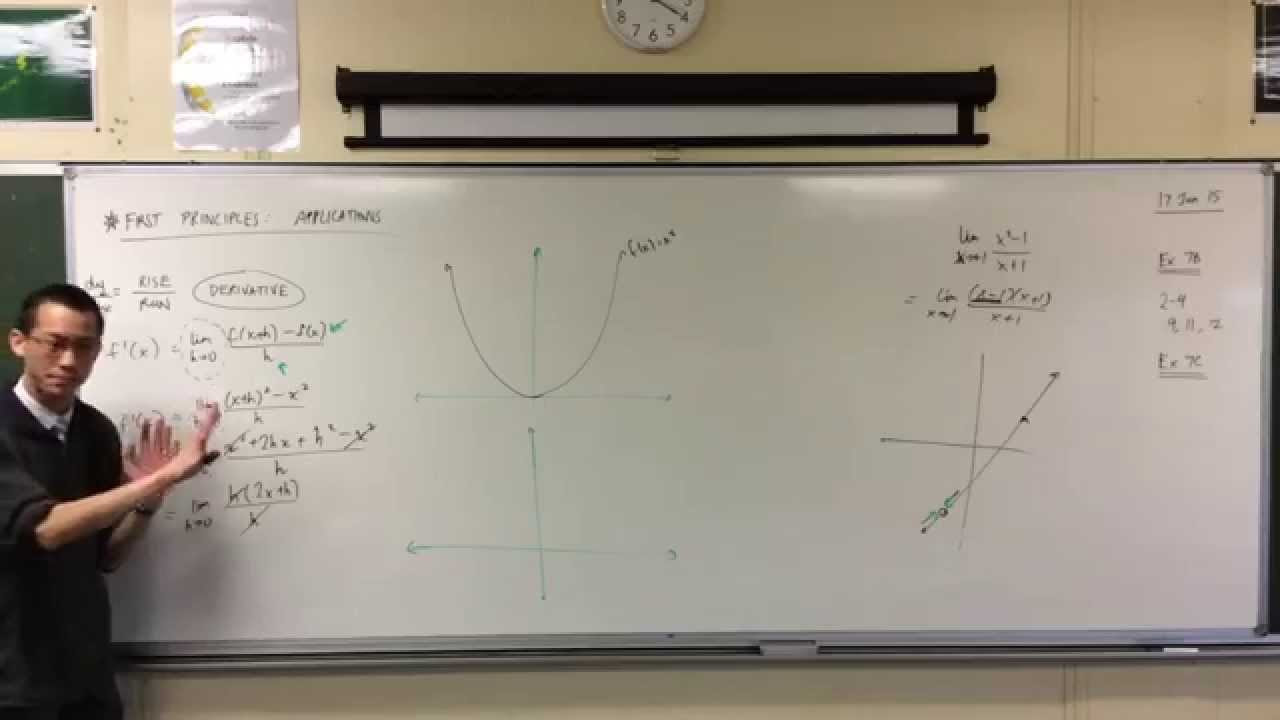
Applying First Principles to x² (1 of 2: Finding the Derivative)
5.0 / 5 (0 votes)