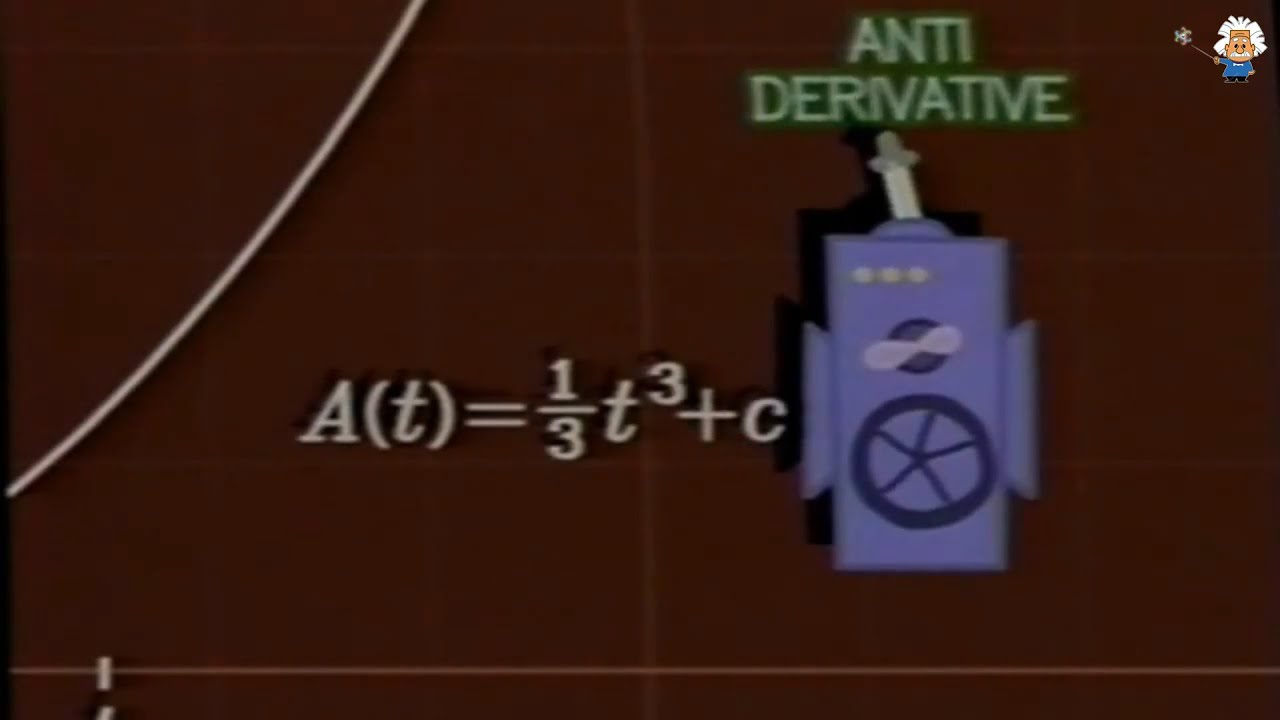Calculus Made EASY! Learning Calculus
Summary
TLDRThis video script demystifies calculus by visually integrating its concepts, focusing on differential and integral calculus. It explains how calculus deals with continuous change, unlike static math, and is crucial for understanding dynamic phenomena across fields like physics and economics. The script clarifies the use of limits to find instantaneous rates of change and areas under curves, highlighting the fundamental theorem of calculus that links differentiation and integration as inverse processes.
Takeaways
- 📚 Calculus is a branch of mathematics that deals with continuous change and is applicable across various fields like physics, biology, and economics.
- 🔍 The video aims to visually integrate the concepts of differential and integral calculus, explaining their relevance and the mathematical equations involved.
- 📈 Calculus is distinct from other branches of mathematics as it focuses on dynamic or continuous change, as opposed to static or constant values.
- 📉 Traditional or static math is limited in its ability to calculate the slope at a specific point on a curve, which is where differential calculus steps in.
- 🎓 Differential calculus, often taught as 'Calculus 1', is designed to find the instantaneous rate of change, such as the slope at any particular point on a curve.
- 📊 Integral calculus, or 'Calculus 2', addresses the challenge of finding the area under a curve when traditional methods fail due to the shape's complexity.
- 🔢 The concept of limits is fundamental to calculus, allowing for dynamic thinking and the calculation of rates of change and areas under curves.
- 🔄 The process of finding the slope at a particular point on a curve involves taking a limit as another point approaches infinitely close to the point of interest.
- 📏 Integral calculus uses the concept of limits to approximate the area under a curve by summing the areas of an infinite number of rectangles that fit under the curve.
- 🔄 The fundamental theorem of calculus reveals the inverse relationship between differentiation and integration, showing how they are interconnected processes.
Q & A
What is calculus and why is it important?
-Calculus is a branch of mathematics that deals with continuous change, often referred to as dynamic math. It is important because it is applicable across various fields such as physics, biology, and economics, providing tools to analyze and solve problems involving change and motion.
What are the two main branches of calculus?
-The two main branches of calculus are differential calculus and integral calculus. Differential calculus focuses on finding the rate of change at a specific point, while integral calculus deals with calculating areas under curves and volumes in three dimensions.
How does calculus differ from other branches of mathematics?
-Calculus differs from other branches of mathematics because it deals with continuous change and motion, rather than static or constant values. It uses concepts like limits and infinitesimals to understand and calculate rates of change and areas under curves.
What is the role of limits in calculus?
-Limits play a fundamental role in calculus by allowing mathematicians to think dynamically rather than statically. They are used to define the concept of a function approaching a certain value infinitely closely, which is essential for understanding rates of change and areas under curves.
Can you explain the concept of a derivative in the context of calculus?
-A derivative in calculus represents the instantaneous rate of change of a function at a particular point. It is found using the concept of limits, where another point is taken infinitely close to the point of interest, and the slope between these two points is calculated.
What is the integral in calculus and how is it related to areas under curves?
-The integral in calculus is used to find the accumulated area under a curve. It is based on the concept of limits, where an infinite number of rectangles are used to approximate the area under the curve. As the number of rectangles approaches infinity, the sum of their areas approaches the actual area under the curve.
How does the concept of a tangent line relate to finding the slope of a curve at a particular point?
-A tangent line is a straight line that touches a curve at a single point without crossing it. The slope of the tangent line at that point is the same as the slope of the curve at that point. Calculus uses the concept of limits to find the slope of a tangent line as it approaches the curve infinitely closely.
What is the fundamental theorem of calculus and why is it important?
-The fundamental theorem of calculus states that differentiation and integration are inverse operations. It links the process of finding the derivative (differential calculus) with the process of finding the integral (integral calculus). This theorem is crucial as it provides a powerful method for evaluating integrals and understanding the relationship between the two branches of calculus.
How does calculus help in understanding the behavior of dynamic systems?
-Calculus helps in understanding the behavior of dynamic systems by providing mathematical tools to analyze rates of change and accumulation of quantities over time. It allows for the modeling of systems that evolve continuously, such as in physics for motion or in economics for growth models.
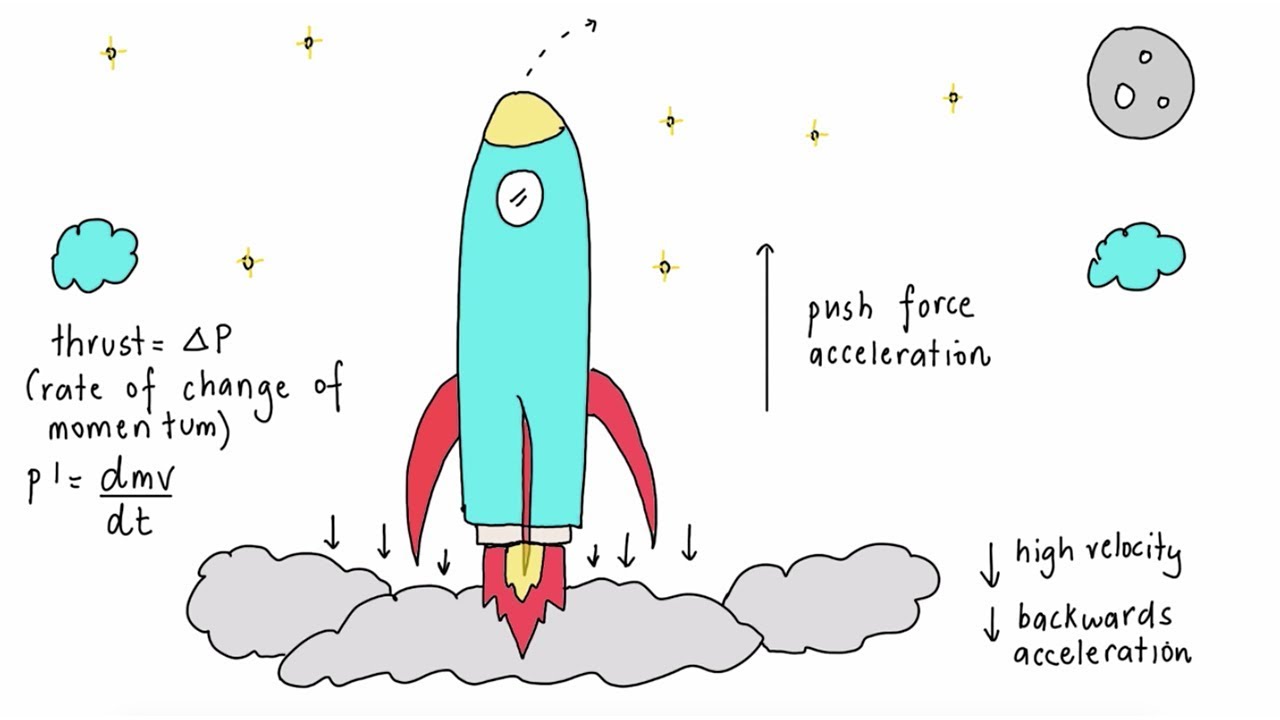
Can you give an example of how calculus is applied in physics?
-In physics, calculus is used to describe the motion of objects. For example, the second law of motion by Newton can be expressed as the derivative of momentum with respect to time, which is the force. Calculus allows physicists to calculate velocities and accelerations from position data, and vice versa.
What is the significance of the concept of 'approaching infinity' in calculus?
-The concept of 'approaching infinity' in calculus is significant because it allows for the analysis of quantities that are changing in an infinitesimal manner. This concept is fundamental in defining derivatives and integrals, enabling the calculation of rates of change and areas under curves without needing exact point coordinates.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)