Angle Bisector & Perpendicular Bisector.avi

Summary

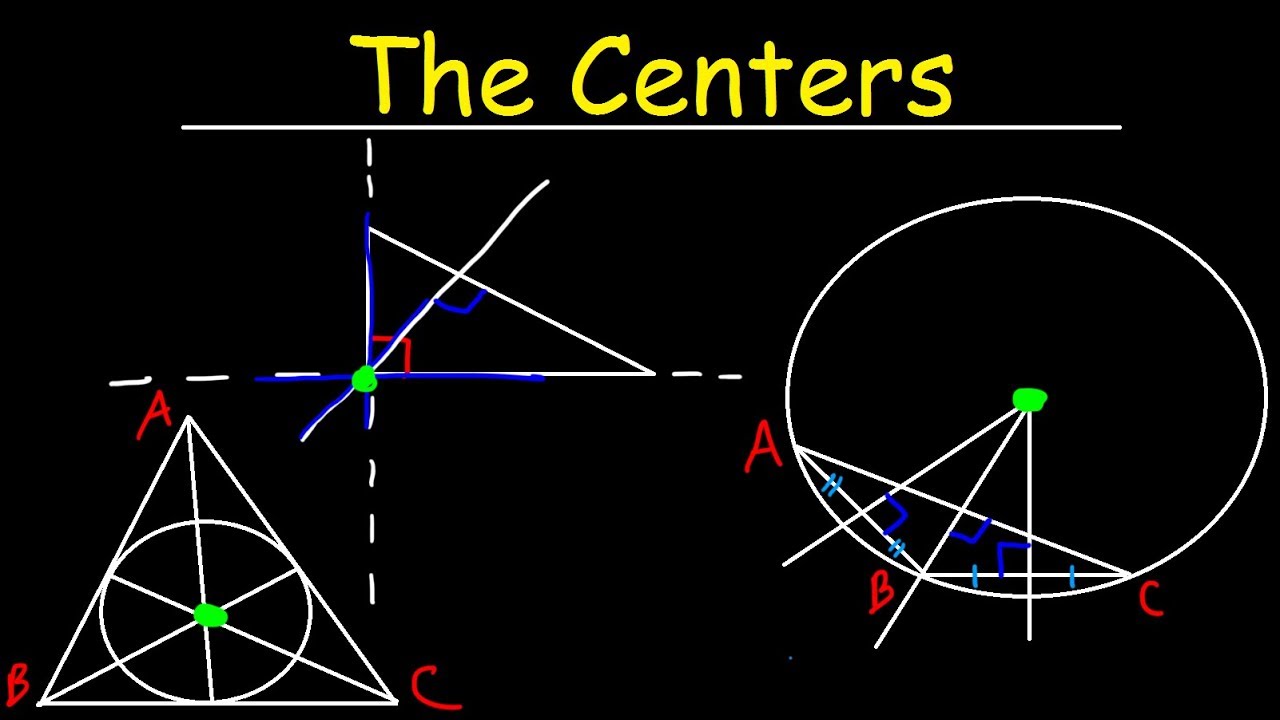
This educational video delves into the concepts of angle bisectors and perpendicular bisectors in the context of triangles. It explains that an angle bisector divides a vertex angle into two equal parts, meeting at the incenter, while a perpendicular bisector cuts a side in half at a 90-degree angle, intersecting at the circumcenter. The video also includes practice problems to illustrate the application of these geometric principles, emphasizing the congruence of angles and segments in solving for unknown variables.

Takeaways

• 📐 An angle bisector is a line segment that bisects one of the vertex angles of a triangle, creating two equal angles.
• 📏 Angle bisectors can be found in three different locations within a triangle, and they all intersect at a common point called the incenter.
• 📍 The incenter is a point of concurrency where the three angle bisectors of a triangle meet.
• 🔍 A perpendicular bisector is a line that is both perpendicular to a side of a triangle and bisects it, passing through its midpoint.
• ⚒️ Perpendicular bisectors have the properties of being at a 90-degree angle and bisecting a segment into two equal lengths.
• 📍 The circumcenter is the point where the three perpendicular bisectors of a triangle intersect, and it can be inside or outside the triangle.
• 🔢 To find the measure of an angle bisected by a line, set the expressions for the two resulting angles equal to each other and solve for the variable.
• 📐 The sum of the two angles created by an angle bisector is equal to the original angle of the triangle.
• 📏 Each triangle can have three perpendicular bisectors, each corresponding to a different side of the triangle.
• 📐 The circumcenter is named for the fact that it is equidistant from all vertices of the triangle, which is a key property in circle geometry.
• 🔢 Solving for the length of a segment bisected by a perpendicular bisector involves using the given angle measure and the properties of right triangles.

Q & A

What is an angle bisector in the context of a triangle?

An angle bisector is a line segment that bisects one of the vertex angles of a triangle, dividing it into two equal angles.

How many angle bisectors can a triangle have?

A triangle can have three angle bisectors, one for each of its angles.

What is the point of concurrency formed by the intersection of all three angle bisectors in a triangle called?

The point of concurrency formed by the intersection of all three angle bisectors is called the incenter.

What is the definition of a perpendicular bisector?

A perpendicular bisector is a line segment that is both perpendicular to a side of a triangle and bisects it, passing through its midpoint.

How does a perpendicular bisector relate to the concepts of a median and an altitude?

A perpendicular bisector combines properties of both a median and an altitude: it goes through the midpoint of a side (like a median) and forms a 90-degree angle (like an altitude).

What is the point of concurrency for the perpendicular bisectors of a triangle known as?

The point of concurrency for the perpendicular bisectors of a triangle is called the circumcenter.

Can the circumcenter of a triangle always be found inside the triangle?

No, the circumcenter can be either inside or outside the triangle, depending on the triangle's shape.

In the practice problem involving an angle bisector, how do we determine the value of x if angle 1 is 6x - 10 and angle 2 is 4x + 12?

Since the angle bisector divides the angle into two equal parts, we set 6x - 10 equal to 4x + 12, solve for x, and find that x equals 11.

What is the measure of angle LMG if it is bisected by the line segment LM?

If angle 1 and angle 2 are both 56 degrees, then angle LMG, which is the sum of angle 1 and angle 2, is 112 degrees.

In the second practice problem, how do we find the length of side BC if the perpendicular bisector ED intersects BC at D and BD is 2x + 4?

First, we solve for x using the equation 7x + 6 = 90, finding x to be 12. Then, we calculate BD as 28 and since D is the midpoint, DC is also 28, making BC equal to 56.

What is the significance of the 90-degree angle in the definition of a perpendicular bisector?

The 90-degree angle in the definition of a perpendicular bisector signifies that the line is perpendicular to the side of the triangle it bisects.