Measures of Central Tendency - Year 1 Statistics [A-level]
Summary
TLDRThis video explains how to calculate the mean, median, and mode for grouped frequency data, using several examples such as the prices of video games and the ages of football squad members. The process involves calculating midpoints for each class interval, adjusting for rounding, and using a calculator for quick computations. Key concepts like the mode (highest frequency interval), median (middle value or 50th percentile), and mean (average value) are covered in detail. The video also highlights the importance of correctly interpreting grouped intervals, especially when data is rounded or approximated.
Takeaways
- 😀 Understand how to calculate the mean, median, and mode for grouped data using frequency tables.
- 😀 The midpoint for a class interval is found by averaging the lower and upper bounds of the interval.
- 😀 The mode is the class interval with the highest frequency, helping to identify the most common range of values.
- 😀 To calculate the median for grouped data, identify the class interval containing the middle value (using cumulative frequency).
- 😀 The formula for the mean is: (Σ midpoint × frequency) / Σ frequency. A calculator can simplify these computations.
- 😀 When working with rounded data (like prices or ages), adjust the interval boundaries to account for rounding errors.
- 😀 For rounded price intervals (e.g., '10 to 19'), rewrite the range as inequalities (e.g., 9.50 ≤ X < 19.50).
- 😀 Always use proper inequality notation when converting class intervals for data like ages or money to avoid overlap or incorrect interpretations.
- 😀 A calculator can be used to quickly calculate the mean and median for grouped data, minimizing manual calculations.
- 😀 The mean and median values are linked to their respective class intervals, so ensure you associate the correct class interval with the median.
- 😀 When working with age data, remember that age is treated as a whole number, so individuals between 14 and 19 years old are all grouped together under the same age range.
Q & A
What is the method to calculate the mean of grouped data in the video?
-To calculate the mean of grouped data, we first find the midpoints of each class interval, multiply each midpoint by the corresponding frequency, then sum these products. Finally, we divide the total by the sum of the frequencies.
Why do we use midpoints for grouped data instead of the exact class boundaries?
-We use midpoints because they represent the most representative value of each interval. Since the exact data points are unknown within the intervals, the midpoint provides a reasonable estimate for calculating statistical measures like the mean.
How do you determine the median from grouped data?
-To find the median, you first identify the class interval where the cumulative frequency reaches or exceeds half of the total frequency. The median corresponds to this class, and it is further refined using linear interpolation if needed.
What does the mode represent in grouped data?
-The mode represents the class interval with the highest frequency. It indicates the most common or frequent value within the dataset.
Why is it important to rewrite class intervals using inequalities when calculating the mean or median?
-Rewriting class intervals using inequalities ensures accuracy when calculating statistical measures. For example, rounding to the nearest pound or year can result in data being grouped differently, and inequalities account for these rounding differences.
How does the rounding of data affect the interval for price calculations in the video?
-The prices are rounded to the nearest pound, which means some values fall just below or above the given interval. By using inequalities (e.g., £9.50 ≤ X < £19.50), we can more accurately represent the range of prices that round to the given class interval.
In the age example, why are the boundaries of the age groups written with inequalities instead of exact values?
-Age is treated differently in this case. For example, if someone is 14.9 years old, they are still considered 14 until their next birthday. Thus, age intervals are represented using strict inequalities, like 15 ≤ X < 20, to exclude the exact boundary of 20.
How do you calculate the midpoints of the intervals in the given examples?
-To calculate the midpoint of a class interval, you add the lower and upper bounds of the interval and then divide by two. For example, for the interval £9.50 to £19.50, the midpoint is (£9.50 + £19.50) / 2 = £14.50.
What are the key differences between the mode, mean, and median in grouped data?
-The mode is the class with the highest frequency, representing the most common data range. The mean is the average, calculated by multiplying midpoints by frequencies and dividing by the total frequency. The median is the middle value, found by identifying the class containing the cumulative frequency that reaches half of the total frequency.
What steps are involved in using a calculator to find the mean and median for grouped data?
-To use a calculator, you input the midpoints of the class intervals and their corresponding frequencies. After entering the data, the calculator computes the mean and median. The median corresponds to the class interval with the midpoint closest to the median value, and the mean is calculated from the sum of the frequency-weighted midpoints.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Statistika #3 Ukuran Pemusatan : Mean - Modus - Median | Kelas X Fase E Kurikulum Merdeka

Statistika Dasar Ukuran Pemusatan Data (Mean, Modus, Median) Data Tunggal dan Data Kelompok

STATISTIKA CARA MENCARI NILAI MEAN, MEDIAN, MODUS DATA KELOMPOK PART 1

Statistika - Ukuran Pemusatan Data (Mean, Median, Modus)
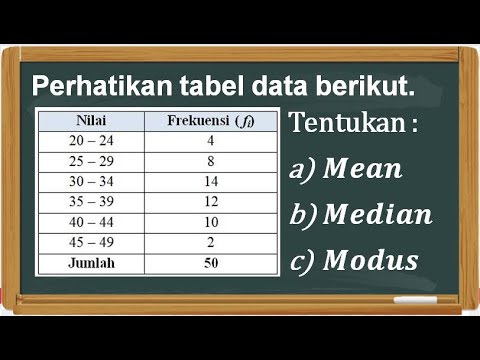
Menentukan Mean, Median, dan Modus Data Kelompok

Ukuran Pemusatan Data Kelompok
5.0 / 5 (0 votes)
