kompleks 01 pendahuluan
Summary
TLDRThis video introduces complex numbers, explaining their necessity when real numbers are insufficient for problem analysis. It emphasizes the components of complex numbers: a real part and an imaginary part, with a focus on the expression z = x + iy, where i represents the square root of -1. The tutorial highlights the development of the concept from real numbers to complex numbers, and the significance of understanding complex operations, particularly in physical problem analysis.
Takeaways
- 😀 Complex numbers arise when real numbers are insufficient for analyzing certain problems.
- 😀 Understanding negative integers and real numbers leads to the concept of complex numbers.
- 😀 The focus of the discussion is on introducing complex numbers and their operations.
- 😀 Complex numbers consist of two parts: the real part and the imaginary part.
- 😀 This development extends the understanding of real numbers into a broader framework.
- 😀 Complex numbers are typically represented as z = x + i * y.
- 😀 In this representation, 'i' is defined as the square root of -1.
- 😀 Both x and y in the equation are real numbers.
- 😀 The study of complex numbers is essential for solving physical problems.
- 😀 The operations involving complex numbers will be explored in detail.
Q & A
What are complex numbers?
-Complex numbers are an extension of real numbers, introduced to address limitations in real number analysis.
Why do we need complex numbers?
-Complex numbers are needed when real numbers are insufficient for solving certain mathematical problems, particularly in physics.
What are the two components of a complex number?
-A complex number consists of a real part and an imaginary part.
How is a complex number typically represented?
-A complex number is typically represented as z = x + i * y, where x is the real part and y is the imaginary part.
What does 'i' represent in complex numbers?
-In complex numbers, 'i' represents the imaginary unit, defined as the square root of -1.
What are the properties of the real and imaginary parts of a complex number?
-Both the real part (x) and the imaginary part (y) of a complex number are real numbers.
How does the introduction of complex numbers relate to earlier number systems?
-Complex numbers build on earlier number systems, such as integers and real numbers, to provide more comprehensive solutions.
In what contexts are complex numbers primarily used?
-Complex numbers are primarily used in various fields of physics and engineering to analyze problems involving oscillations, waves, and electrical circuits.
What is the significance of understanding complex numbers in mathematical analysis?
-Understanding complex numbers is crucial for advanced mathematical analysis and problem-solving in multiple scientific disciplines.
Can you give an example of a complex number?
-An example of a complex number is z = 3 + 4i, where 3 is the real part and 4 is the imaginary part.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

APA ITU BILANGAN KOMPLEKS ? (Materi Kurikulum Merdeka)

3.1 Bilangan Real (Pendahuluan)
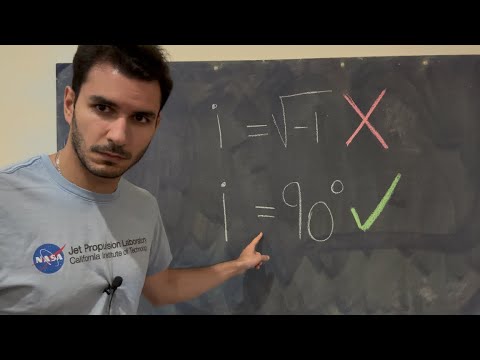
Imaginary numbers aren't imaginary

Numbers in Python Version 2 || Python Tutorial || Learn Python Programming

Eps.1 KALKULUS 1: Pendahuluan Kalkulus - Bilangan Real, Estimasi, dan Logika

Números imaginarios | Introducción y potencias de "i"
5.0 / 5 (0 votes)
