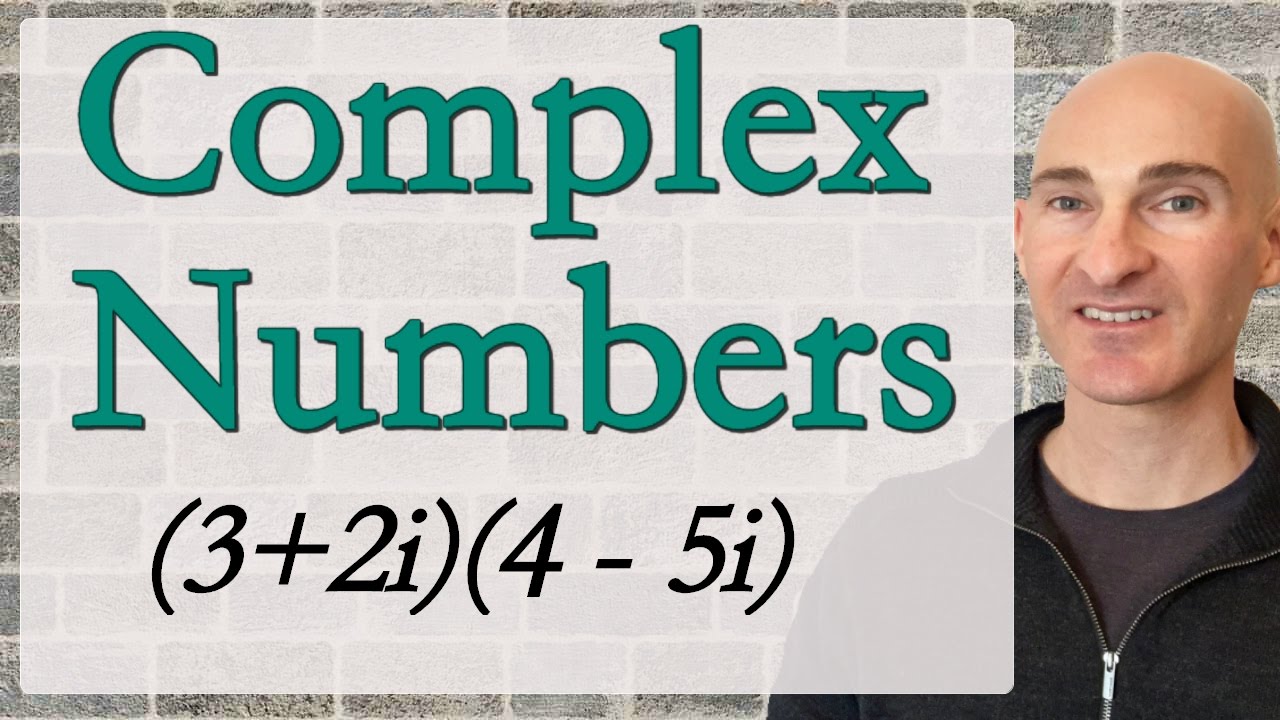Números imaginarios | Introducción y potencias de "i"

Summary

In this video, the speaker introduces complex numbers, starting with the concept of imaginary numbers, particularly the square root of -1, denoted as 'i'. The script explores the historical development of imaginary numbers, highlighting their initial perception as strange and their eventual formalization by mathematician Euler in the 18th century. The speaker demonstrates how powers of 'i' behave, illustrating patterns and properties when 'i' is raised to various exponents, which are useful for understanding complex number multiplication. The video is a comprehensive and engaging introduction to the foundations of complex numbers.

Takeaways

• 😀 The concept of imaginary numbers, particularly the square root of -1, has been studied since ancient times.
• 😀 The square root of 9 is both 3 and -3, since both satisfy the equation (3 * 3 = 9) and (-3 * -3 = 9).
• 😀 Squaring any real number results in a positive value, whether the number is positive or negative.
• 😀 Imaginary numbers were once considered strange and without practical use, with some mathematicians in the 17th century describing them as 'between being and nothingness'.
• 😀 Euler, a prominent mathematician, gave the imaginary number (√-1) the symbol 'i' in 1777, helping to popularize the concept.
• 😀 Any number or variable raised to the power of 0 equals 1, including the imaginary number 'i' (i^0 = 1).
• 😀 Raising 'i' to the first power gives 'i' itself (i^1 = i).
• 😀 i^2 equals -1, which is a key property of imaginary numbers, since √-1 raised to the second power eliminates the square root.
• 😀 i^3 is equal to -i, as the result of multiplying i^2 (-1) by i gives -i.
• 😀 i^4 equals 1 because i^2 is -1, and multiplying two -1s gives a positive 1.
• 😀 The powers of i follow a repeating cycle: i^1 = i, i^2 = -1, i^3 = -i, i^4 = 1, and this cycle repeats every 4 powers.

Q & A

What is the significance of the number √(-1)?

The number √(-1), also known as 'i', is called an imaginary number. It was first encountered by mathematicians due to its inability to fit into the set of real numbers, which led to its development as a fundamental concept in complex numbers.

Why were ancient mathematicians confused by √(-1)?

Ancient mathematicians were confused by √(-1) because when squared, any real number (positive or negative) results in a positive number. There was no real number whose square was negative, so the idea of √(-1) was considered strange and not immediately understood.

Who first formalized the concept of imaginary numbers?

The concept of imaginary numbers was formalized by Euler in 1777, who gave the symbol 'i' to represent √(-1), a number previously considered mysterious by mathematicians.

What does 'i' represent in mathematics?

'i' represents the imaginary unit, which is defined as the square root of -1. It is a key component in complex numbers, which have both a real and an imaginary part.

What happens when 'i' is raised to the power of 0?

When 'i' is raised to the power of 0, it equals 1, following the rule that any non-zero number raised to the power of 0 is 1.

What is the result of 'i' raised to the power of 1?

When 'i' is raised to the power of 1, the result is simply 'i' itself, as any number raised to the first power is the number itself.

What does 'i' squared equal?

When 'i' is squared (i.e., 'i' raised to the power of 2), the result is -1, because i is defined as the square root of -1, and squaring it eliminates the square root.

How can we calculate 'i' raised to higher powers like 3 or 4?

To calculate higher powers of 'i', we can use patterns. For example, 'i' raised to the power of 3 equals -i, and 'i' raised to the power of 4 equals 1. The powers of 'i' repeat in a cycle of 4: i, -1, -i, and 1.

What is the result of 'i' raised to the power of 5?

When 'i' is raised to the power of 5, it simplifies to 'i'. This is because powers of 'i' repeat every four terms (i.e., i^1, i^2, i^3, i^4), and after completing the cycle, i^5 is equivalent to i^1.

How does the concept of powers of 'i' relate to complex numbers?

The powers of 'i' are fundamental when working with complex numbers, as they are used to calculate the behavior of complex numbers in various operations, such as multiplication and division. Understanding these powers is crucial for performing operations on complex numbers.