Solving Systems of Equations By Graphing
Summary
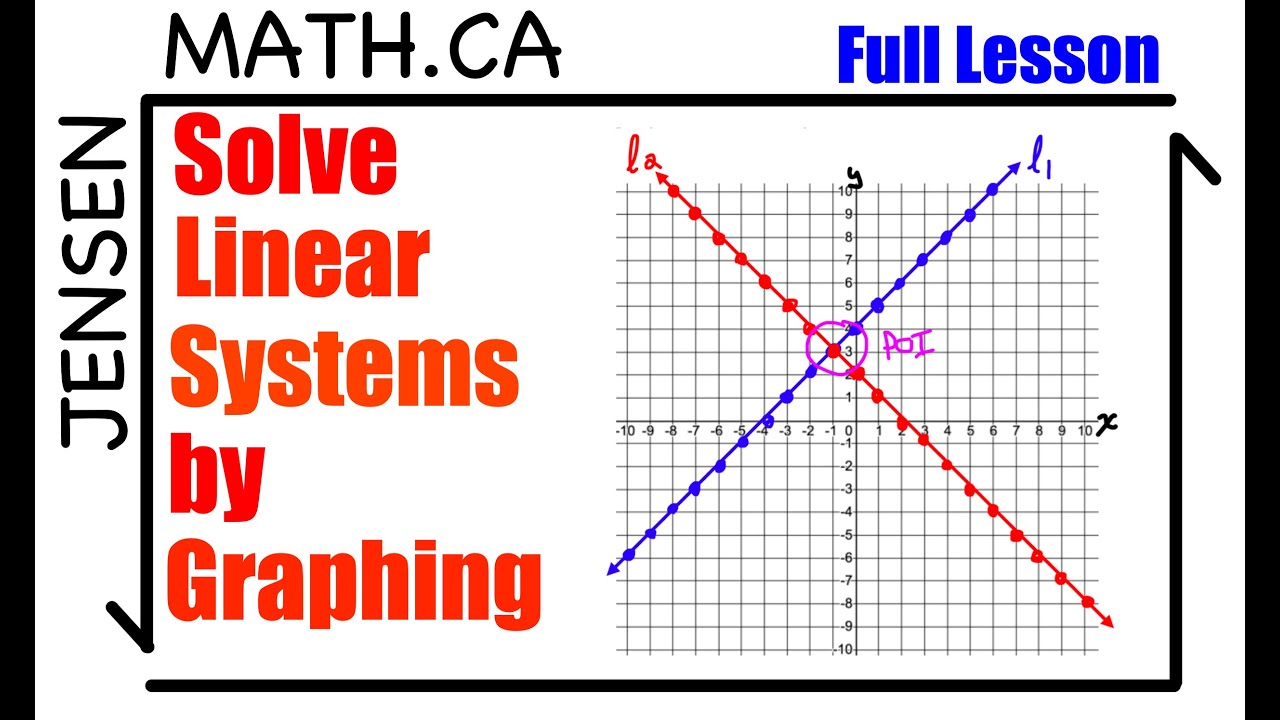
TLDRIn this lesson, the instructor demonstrates how to solve a system of equations by graphing. The equations y = 2x - 3 and y = -2/3x + 5 are graphed to identify their point of intersection, which is the solution to the system. The instructor emphasizes the importance of using a large graph for clarity and walks through the process of finding key points based on the slope and y-intercept. Additionally, the solution is verified through substitution, confirming that the intersection point is (3, 3). This comprehensive approach reinforces both graphical and algebraic methods for solving equations.
Takeaways
- 📊 Graphing is an effective method for solving systems of equations.
- 📏 The first equation given is in slope-intercept form: y = 2x - 3.
- 🔍 The slope of the first equation is 2, and the y-intercept is -3.
- ⬆️ To plot the first equation, start at the y-intercept and use the slope to find additional points.
- 📈 The second equation is y = -2/3x + 5, which also follows slope-intercept form.
- 🎯 The y-intercept of the second equation is 5, with a slope of -2/3.
- 🗺️ Finding the point of intersection of the two graphs provides the solution to the system of equations.
- ✅ The point of intersection determined through graphing is (3, 3).
- 🔄 Substitution is another method to solve for the intersection of the equations.
- ✖️ Eliminating fractions in equations can simplify the solving process.
Q & A
What are the two equations being solved in this lesson?
-The two equations are y = 2x - 3 and y = -2/3x + 5.
How do you determine the point of intersection when graphing two equations?
-The point of intersection is found by graphing both equations on a coordinate plane and identifying where the two lines cross.
What is the slope of the first equation, and how is it used?
-The slope of the first equation (y = 2x - 3) is 2, which indicates that for every 1 unit you move to the right on the x-axis, you move up 2 units on the y-axis.
What is the significance of the y-intercept in these equations?
-The y-intercept indicates where the line crosses the y-axis. For the first equation, the y-intercept is -3, meaning it starts at the point (0, -3) on the graph.
How do you graph the second equation?
-To graph the second equation (y = -2/3x + 5), start at the y-intercept of 5 on the y-axis, then use the slope of -2/3 to find additional points by moving 3 units right and 2 units down.
What is the calculated point of intersection for these equations?
-The calculated point of intersection for the two equations is (3, 3).
What method is used to verify the solution after graphing?
-The solution is verified using substitution by replacing y in one equation with the expression from the other equation and solving for x.
How do you eliminate fractions when solving the equation?
-You can eliminate fractions by multiplying every term in the equation by a common denominator, which simplifies the calculations.
What does the result x = 3 indicate in the context of the equations?
-The result x = 3 indicates the x-coordinate of the point of intersection, which is used to find the corresponding y-coordinate.
Why is it beneficial to draw a larger graph?
-Drawing a larger graph allows for better visualization of the intersection point and makes it easier to plot points accurately.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

SOLVING SYSYEM OF NONLINEAR EQUATIONS || PRECALCULUS
Solve a Linear System by Graphing | jensenmath.ca | grade 10

SPLTV Kelas 10 Kurikulum Merdeka

MaTek 1 Menggambar grafik Fungsi Linier #Part 6#Matematika Teknik 1

PERSAMAAN KUADRAT part ZERO-ONE

Kurikulum Merdeka Matematika Kelas 9 Bab 1 Sistem Persamaan Linear Dua Variabel
5.0 / 5 (0 votes)
