Conversiones entre sistemas de numeración (Binario, octal y hexadecimal a decimal)
Summary
TLDREste video educativo explica los sistemas de numeración posicional, con énfasis en decimal, octal, binario y hexadecimal. Se describe cómo el valor de una cifra varía según su posición y la base del sistema. A través de ejemplos prácticos, se muestra cómo convertir números de estos sistemas al decimal y viceversa, utilizando potencias y multiplicaciones para calcular el valor de cada cifra. El video también ofrece recursos para practicar estas conversiones, promoviendo el aprendizaje y la comprensión de conceptos fundamentales en matemáticas y programación.
Takeaways
- 🔢 Los sistemas de numeración posicional como decimal, octal y binario dependen del valor del símbolo y su posición en la notación.
- 📏 En el sistema decimal, cada posición a la izquierda del símbolo se multiplica por 10, incrementando la potencia de 10 (100, 1000, 10,000, etc.).
- 📈 El valor de cada cifra en un sistema decimal se puede expresar como 10 elevado a una potencia que corresponde a su posición.
- 📘 Para convertir de octal a decimal, se multiplica el valor de cada cifra por 8 elevado a la potencia correspondiente a su posición.
- 🔄 En el sistema binario, cada posición se multiplica por 2, y la base es 2, lo que simplifica los cálculos ya que solo hay símbolos 0 y 1.
- 📌 La suma de los productos de los valores de las cifras y sus posiciones en binario da el valor decimal equivalente.
- 💡 Los sistemas hexadecimales utilizan una base de 16 y símbolos que incluyen dígitos del 0 al 9 y letras de A a F para representar valores del 10 al 15.
- 🖊️ Al convertir de hexadecimal a decimal, se multiplica el valor decimal de cada símbolo por 16 elevado a la potencia correspondiente a su posición.
- 🔧 Se pueden realizar conversiones de sistemas de numeración sin una calculadora, pero también se pueden usar para facilitar el proceso.
- 🌐 Para practicar conversiones de sistemas de numeración, se recomienda visitar recursos en línea como 'programación simple'.
Q & A
¿Qué es un sistema de numeración posicional?
-Un sistema de numeración posicional es un método de representar números en el que el valor de cada dígito depende del valor del símbolo y su posición dentro del número.
¿Cómo se determina el valor de una cifra en el sistema decimal?
-En el sistema decimal, el valor de una cifra se determina multiplicando el valor del símbolo (0-9) por la potencia de 10 que corresponde a su posición, comenzando desde la izquierda.
¿Cuál es la base del sistema decimal?
-La base del sistema decimal es 10, lo que significa que cada posición a la izquierda se multiplica por 10.
¿Cómo se convierte un número del sistema octal al decimal?
-Para convertir un número del sistema octal al decimal, se multiplica el valor de cada cifra (0-7) por 8 elevado a la potencia correspondiente a su posición, comenzando desde la derecha, y luego se suman los resultados.
¿Qué es la base del sistema octal?
-La base del sistema octal es 8, por lo que cada posición a la izquierda se multiplica por 8.
¿Cómo se determina el valor de una cifra en el sistema binario?
-En el sistema binario, el valor de una cifra se determina multiplicando el valor del símbolo (0 o 1) por 2 elevado a la potencia correspondiente a su posición, comenzando desde la derecha.
¿Cuál es la base del sistema binario?
-La base del sistema binario es 2, lo que significa que cada posición a la izquierda se multiplica por 2.
¿Cómo se convierte un número del sistema hexadecimal al decimal?
-Para convertir un número del sistema hexadecimal al decimal, se multiplica el valor de cada cifra (0-9 y A-F) por 16 elevado a la potencia correspondiente a su posición, comenzando desde la derecha, y luego se suman los resultados.
¿Qué es la base del sistema hexadecimal?
-La base del sistema hexadecimal es 16, por lo que cada posición a la izquierda se multiplica por 16.
¿Cómo se puede simplificar la conversión de un número binario a decimal?
-Se puede simplificar la conversión de un número binario a decimal ignorando las posiciones con el símbolo 0 (ya que cualquier número multiplicado por 0 da 0) y sumando solo los valores de las posiciones con el símbolo 1.
¿Dónde se pueden practicar ejercicios de conversiones de sistemas numéricos?
-Se pueden practicar ejercicios de conversiones de sistemas numéricos en la página web 'programación simple', como se menciona en el guion del video.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Sistemas de Numeración

Sistemas de Numeración (DECIMAL, BINARIO y HEXADECIMAL) - Explicación y tabla comparativa
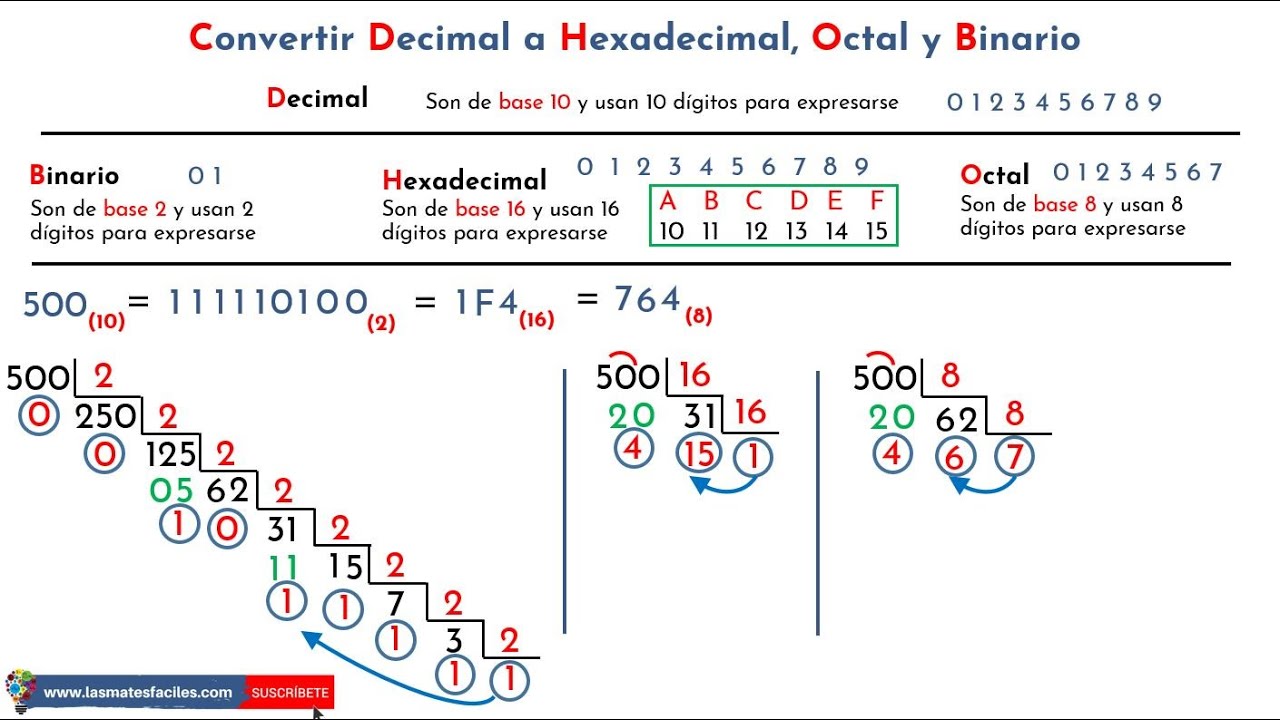
Convertir: Decimal a Binario - Decimal a Hexadecimal - Decimal a Octal - Ejemplos paso a paso!

Convertidor Binario a Decimal LabVIEW Parte 1

Sistemas numéricos: Binario, Decimal y Hexadecimal

Convertir Binario a Decimal
5.0 / 5 (0 votes)
