Introducción a Trigonometría

Summary

El script ofrece una introducción al curso de trigonometría, explicando conceptos fundamentales como el ángulo trigonométrico, el sistema de medida angular y los triángulos rectángulos. Seguidamente, se exploran las relaciones trigonométricas en triángulos notables, como el 3-4-5 y el 30-60-90, y se calculan las seis razones trigonométricas para ángulos específicos. El video finaliza con una guía para calcular y recordar estas razones de manera eficiente, utilizando la palabra 'SOCA' y proporcionando una tablita de valores para el ángulo de 37 grados.

Takeaways

• 📚 La introducción al curso de trigonometría comienza con la definición de un ángulo trigonométrico generado por la rotación de una rayo alrededor de su origen.
• 📐 Se explica que el ángulo puede medirse en diferentes sistemas: sexagesimal (grados), centesimal (grados centesimales) y radial (radianes).
• 🔄 La rotación de la rayo en sentido horario genera ángulos con medición negativa, mientras que en sentido antihorario la medición es positiva.
• 🔢 Un ángulo completo de 360 grados en sexagesimal equivale a 400 grados centesimales y a 2π radianes.
• ➗ Para convertir grados sexagesimales a radianes, se utiliza la fórmula de conversión o el método de la regla de tres, recordando que 360 grados sexagesimales equivalen a 2π radianes.
• 📈 Se introducen los triángulos rectángulos, destacando que tienen tres lados y tres ángulos, uno de los cuales es de 90 grados.
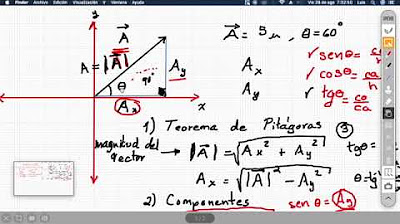
• 📐 El teorema de Pitágoras se aplica en triángulos rectángulos para relacionar la hipotenusa con los catetos (a^2 + b^2 = c^2).
• 🔢 En triángulos rectángulos, la suma de los ángulos internos es siempre 180 grados, siendo dos de ellos complementarios y sumando 90 grados.
• 🌟 Se presentan triángulos notables como el 3-4-5, el 30-60-90 y el 45-45, que tienen relaciones fijas entre sus ángulos y lados.
• 📈 Las razones trigonométricas se definen como la relación entre los lados de un triángulo rectángulo y se asocian con los ángulos del triángulo: seno, coseno, tangente, cotangente, secante y cosecante.
• 📝 Se ilustra cómo calcular las razones trigonométricas de ángulos comunes, como el 37°, utilizando los triángulos notables y sus proporciones de lados.

Q & A

¿Qué es un ángulo trigonométrico y cómo se forma?

Un ángulo trigonométrico es una figura generada cuando un rayo gira alrededor de su origen, tomando este origen como centro de giro. Se forma al mover el rayo de su posición inicial a una posición final.

¿Cuál es la diferencia entre el lado inicial y el lado final de un ángulo trigonométrico?

El lado inicial es la posición que tenía el rayo antes de girar, mientras que el lado final es la posición que toma el rayo después de completar la rotación alrededor del vértice.

¿Cómo se miden los ángulos trigonométricos y cuáles son las unidades de medida utilizadas?

Los ángulos trigonométricos se miden utilizando sistemas de medida angular. Los sistemas más comunes son el sexagesimal (grados), el centesimal (grados centesimales) y el radial (radianes).

¿Qué representa un ángulo negativo en el sentido de las agujas del reloj y un ángulo positivo en sentido contrario a las agujas del reloj?

Un ángulo negativo se representa cuando el rayo gira en el sentido de las agujas del reloj (sentido horario), mientras que un ángulo positivo se representa cuando el rayo gira en sentido contrario a las agujas del reloj (sentido antihorario).

¿Cuál es la medida de un ángulo completo en los diferentes sistemas de medida angular?

Un ángulo completo, es decir, un radio que da una vuelta completa alrededor de su origen, mide 360 grados en el sistema sexagesimal, 400 grados en el sistema centesimal y 2 pi radianes en el sistema radial.

¿Cómo se convierte 18 grados sexagesimales a radianes utilizando la regla de tres?

Para convertir de grados sexagesimales a radianes, se utiliza la relación de que 360 grados sexagesimales equivalen a 2 pi radianes. Se establece una proporción donde 360 grados sexagesimales están relacionados con 2 pi radianes, y se busca el valor de x para 18 grados sexagesimales, resultando en (18 * 2 pi) / 360.

¿Qué es un triángulo rectángulo y cómo se identifican sus ángulos y lados?

Un triángulo rectángulo es un triángulo que tiene un ángulo de 90 grados. Sus lados son identificados como los catetos (opuestos y adyacentes al ángulo recto) y la hipotenusa (el lado opuesto al ángulo de 90 grados, que es el más largo).

¿Cómo se relacionan los ángulos internos de un triángulo rectángulo?

Los ángulos internos de un triángulo rectángulo siempre suman 180 grados. En el caso de un triángulo rectángulo, uno de los ángulos es de 90 grados, por lo que los otros dos ángulos son complementarios y suman 90 grados.

¿Cuál es la fórmula del teorema de Pitágoras y cómo se aplica en un triángulo rectángulo?

La fórmula del teorema de Pitágoras es a^2 + b^2 = c^2, donde a y b son los catetos del triángulo rectángulo y c es la hipotenusa. Se aplica para calcular el valor de uno de los lados si se conocen los otros dos.

¿Qué son los triángulos notables y cómo se relacionan sus ángulos y lados?

Los triángulos notables son aquellos con relaciones fijas entre sus ángulos y lados, como los triángulos de 37°-53°-90°, 30°-60°-90° y 45°-45°-90°. Los lados de estos triángulos son proporcionales a ciertas cantidades, como 3-4-5, 1-√3-2 y 1-1-√2 respectivamente.

¿Cómo se calculan las razones trigonométricas de un ángulo en un triángulo rectángulo?

Las razones trigonométricas se calculan dividiendo el cateto opuesto (seno), el cateto adyacente (coseno) o ambos catetos (tangente y cotangente) entre la hipotenusa (secante y cosecante) del ángulo en cuestión dentro del triángulo rectángulo.

¿Cómo se relacionan las razones trigonométricas de los ángulos de 37° y 53° en un triángulo 37-53-90?

Dado que 37° y 53° son ángulos complementarios, las razones trigonométricas de uno son las recíprocas de las del otro. Por ejemplo, si el seno de 37° es 3/5, el coseno de 53° será 4/5, y viceversa.

¿Qué es la palabra mágica 'SOCA' y cómo se utiliza para recordar las fórmulas de las razones trigonométricas?

La palabra mágica 'SOCA' es una acrónimo que ayuda a recordar las primeras letras de las seis razones trigonométricas: Seno, Coseno, Tangente, Cotangente, Secante y Cosecante. Se utiliza para facilitar el recuerdo de las fórmulas asociadas a cada una.