Máximos y mínimos de una función | Ejemplo 1
Summary
TLDREn este video, el profesor imparte un curso sobre cómo encontrar los máximos y mínimos de una función utilizando derivadas. Seguidamente, explica los cuatro pasos fundamentales: derivar la función, encontrar donde la derivada es cero, calcular el valor de la función en ese punto y determinar si es un máximo o mínimo. Utiliza un gráfico y un ejemplo práctico para ilustrar el proceso. Finalmente, ofrece un ejercicio para que los estudiantes practiquen y recomienda ver el curso completo para una comprensión más profunda del tema.
Takeaways
- 📚 El curso trata sobre cómo encontrar los máximos y mínimos de una función utilizando derivadas.
- 📈 Se proporciona un gráfico para ayudar a entender el proceso, aunque no es obligatorio para encontrar los extremos.
- 🔍 Los cuatro pasos clave para encontrar los máximos y mínimos son: derivar la función, encontrar donde la derivada es cero, calcular el valor de la función en ese punto y determinar si es un máximo o mínimo.
- 📝 La derivada es fundamental porque indica la pendiente de la función en un punto dado y es cero en los puntos críticos.
- ✍️ Al resolver la derivada igualada a cero, se obtiene una ecuación de primer grado que ayuda a encontrar los puntos críticos.
- 🔢 Para determinar si un punto crítico es un máximo o un mínimo, se evalúa el signo de la derivada a la izquierda y derecha del punto.
- 📉 Si la función es decreciente a la izquierda y creciente a la derecha del punto crítico, entonces se tiene un mínimo.
- 📈 El método de la segunda derivada es una técnica para determinar si un punto crítico es un máximo o un mínimo; si la segunda derivada en el punto crítico es positiva, es un mínimo.
- 📚 En el caso de funciones cuadráticas, si el término de \( x^2 \) está acompañado de un número negativo, la parábola se inclina hacia abajo, indicando un máximo.
- 📝 Se menciona que para funciones cuadráticas no es necesario el cuarto paso si se conoce el signo del término cuadrático.
- 👍 El instructor anima a los estudiantes a suscribirse, comentar, compartir y dar 'like' al video si les gustó el contenido.
Q & A
¿Qué es el objetivo principal del curso de derivadas mencionado en el guion?
-El objetivo principal del curso es enseñar a los estudiantes cómo encontrar los máximos y mínimos de una función.
¿Por qué es importante entender los pasos para encontrar los máximos y mínimos de una función y no simplemente memorizarlos?
-Es importante comprender los pasos para que el proceso sea más fácil de entender y aplicar en diferentes situaciones, en lugar de tratar de recordarlos sin contexto.
¿Cuál es el primer paso para encontrar los máximos o mínimos de una función según el guion?
-El primer paso es derivar la función, ya que la derivada nos permite encontrar la pendiente en cualquier punto.
¿Qué representa la derivada de una función en el contexto de encontrar máximos y mínimos?
-La derivada representa la pendiente de la función, y en los puntos de máximo o mínimo, la pendiente es cero.
¿Cómo se determina si un punto crítico es un máximo, un mínimo o ninguno de los dos?
-Se determina evaluando si la función es creciente o decreciente a los lados del punto crítico o utilizando el método de la segunda derivada.
¿Qué métodos se mencionan en el guion para determinar si un punto crítico es un máximo o un mínimo?
-Se mencionan dos métodos: el primero es observar si la función es creciente o decreciente a los lados del punto crítico, y el segundo es el método de la segunda derivada.
¿Qué es la segunda derivada y para qué se usa en el contexto del guion?
-La segunda derivada es la derivada de la primera derivada y se usa para determinar si un punto crítico es un máximo o un mínimo, ya que si es positiva, indica un mínimo, y si es negativa, indica un máximo.
¿Cómo se determina si una parábola es de máximo o mínimo en una función cuadrática sin necesidad de calcular la segunda derivada?
-Se observa el signo del término que acompaña al término de x al cuadrado; si es negativo, la parábola tiene un máximo, y si es positivo, tiene un mínimo.
¿Qué es una parábola y cómo se relaciona con los máximos y mínimos de una función?
-Una parábola es la gráfica de una función de segundo grado (cuadrática), y su forma indica si la función tiene un máximo o un mínimo; una parábola ascendente tiene un mínimo y una parábola descendente tiene un máximo.
¿Por qué el guion enfatiza la importancia de comprender el proceso en lugar de solo ver el gráfico de la función?
-El guion enfatiza la importancia de la comprensión para que los estudiantes puedan aplicar los conceptos en diferentes situaciones y no depender únicamente de la visualización gráfica.
¿Qué se sugiere hacer al final del guion para fortalecer la comprensión de los conceptos?
-Se sugiere que los estudiantes practiquen con ejercicios y vean el curso completo o algunos vídeos recomendados para profundizar en el tema.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Máximos y mínimos de una función | Ejemplo 2

Derivadas Máximos, Mínimos, Crecimientos y Concavidad

Máximo relativo, mínimo relativo, intervalos de crecimiento y decrecimiento de una función

Como resolver problemas de aplicación de máximos o mínimos
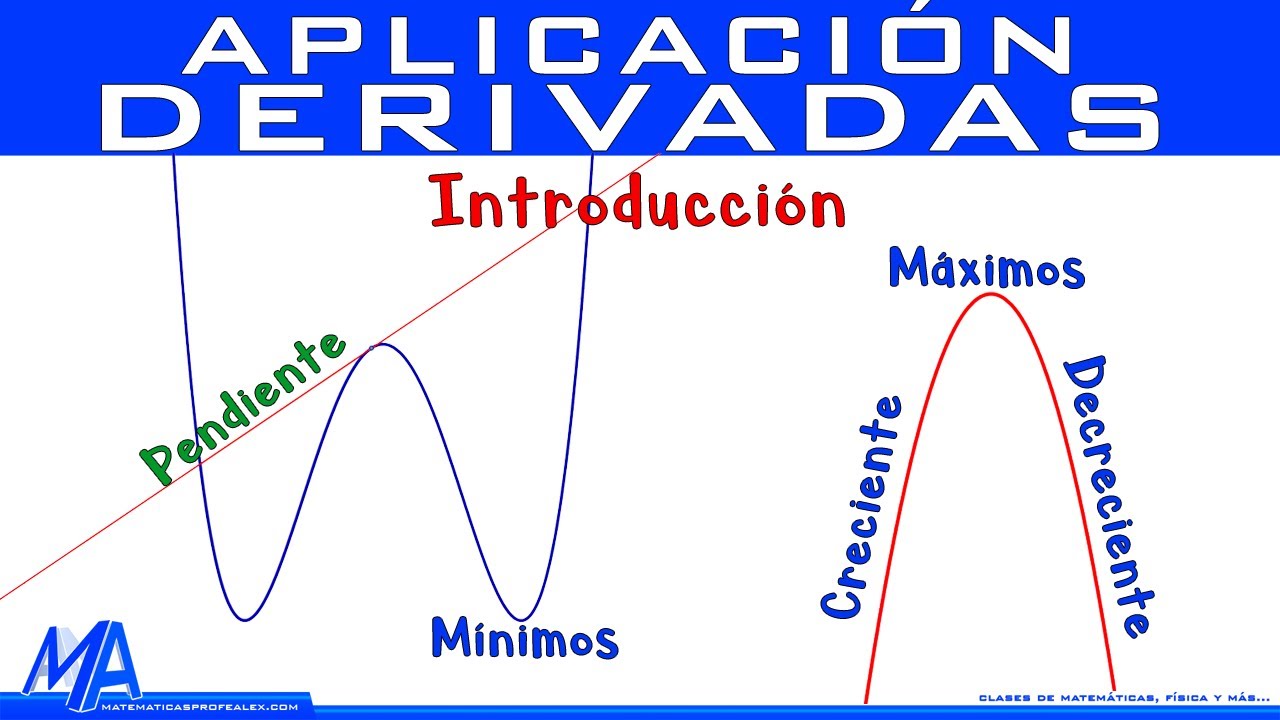
Aplicación de la derivada Introducción

Derivada de Logaritmo Natural | Ejemplo 1
5.0 / 5 (0 votes)
