Máximo relativo, mínimo relativo, intervalos de crecimiento y decrecimiento de una función
Summary
TLDRThe transcript guides viewers through the process of analyzing a function by finding critical points, determining intervals of increase and decrease, and identifying relative maxima and minima. Using the quotient rule for differentiation, the first derivative of the function is calculated and set equal to zero to find the critical points. Then, intervals are tested to determine where the function is increasing or decreasing. Finally, by analyzing the sign changes of the derivative, relative maxima and minima are identified. The result highlights key points for understanding the function's behavior and provides a step-by-step approach for solving similar problems.
Takeaways
- 😀 The derivative of a function is used to find the critical points, intervals of increase/decrease, and relative maxima/minima.
- 😀 To determine the critical points, the derivative of the function is set equal to zero.
- 😀 The quotient rule is applied for differentiating a function that is a quotient of two functions.
- 😀 The quotient rule formula involves squaring the denominator, multiplying the numerator's derivative by the denominator, and subtracting the numerator multiplied by the derivative of the denominator.
- 😀 After deriving the function, the next step is to set the derivative equal to zero to find the critical points, which are the values of x where the derivative is zero.
- 😀 Critical points in this example are found at x = 0 and x = -2.
- 😀 The intervals for analyzing the behavior of the function are created by placing the critical points on a number line.
- 😀 The function’s behavior (increasing or decreasing) is determined by testing a point in each interval and evaluating the sign of the derivative.
- 😀 The first interval (-∞, -2) shows the function is decreasing, the second interval (-2, 0) shows the function is increasing, and the third interval (0, ∞) shows the function is decreasing.
- 😀 A relative minimum occurs at x = -2, where the function changes from decreasing to increasing.
- 😀 A relative maximum occurs at x = 0, where the function changes from increasing to decreasing.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

CD.28 Criterio de la segunda derivada para máximos y mínimos. Incluye gráfico. Parte 1.

APLICACIÓN DE LA DERIVADA AL TRAZADO DE CURVAS - Ejercicio 2

Differentiation (Maxima and Minima)
Análisis de gráfica. Primera derivada
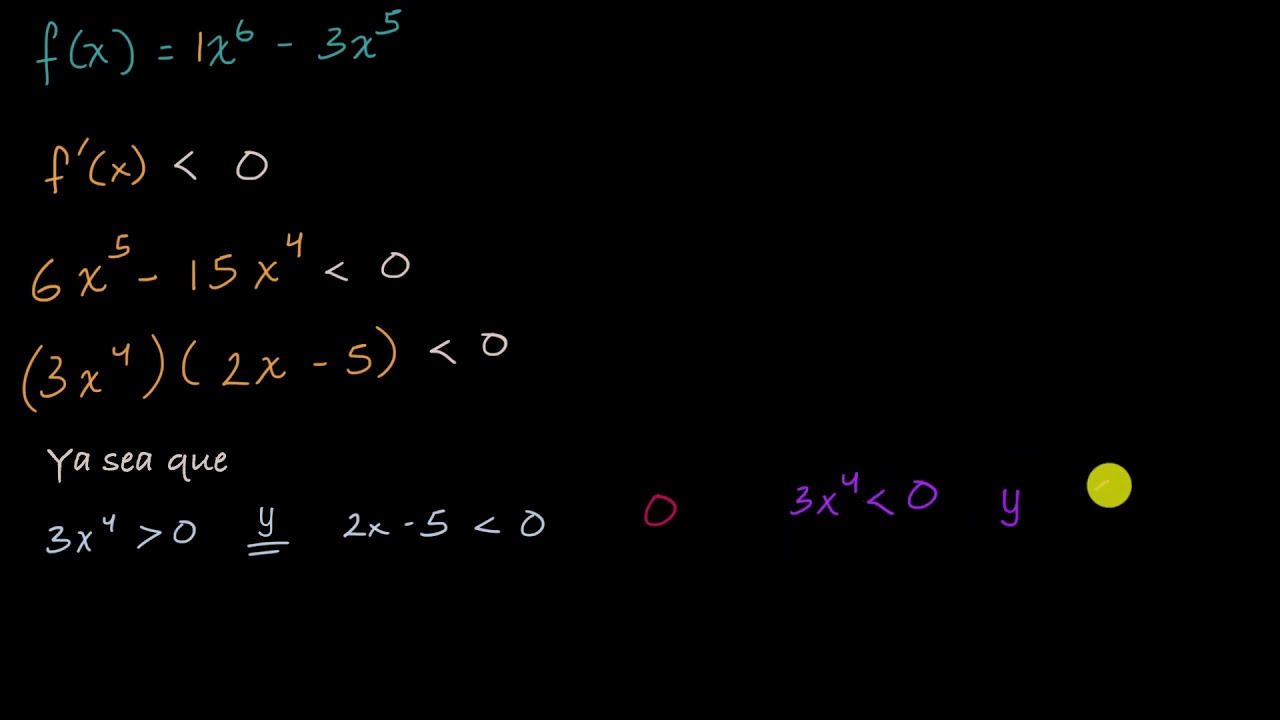
Encontrar el intervalo donde la función es decreciente | Cálculo
✅👉 Encontrar Maximos y Minimos Locales en una Grafica

Fungsi naik, fungsi turun, stasioner, maksimum/minimum | Aplikasi turunan part. 1
5.0 / 5 (0 votes)