Integration By Parts
Summary
TLDRThis educational video script covers the technique of integration by parts to solve various integral problems. It explains the process step by step, starting with the integral of x times e^x and progressing to more complex examples such as the integral of x^2 ln(x) and combinations of exponential and trigonometric functions. The script also tackles integrals involving logarithmic functions and provides a method to solve definite integrals, exemplified by e^(3x)cos(4x). Each example builds on the previous, reinforcing the concept of integration by parts for students to master calculus integration.
Takeaways
- 📚 Integration by parts is a fundamental technique for solving integrals of products of functions, expressed as ∫udv = uv - ∫vdu.
- 🔍 Choosing 'u' and 'dv' wisely is crucial; typically, 'u' is chosen to simplify when differentiated, and 'dv' is chosen to be easily integrable.
- 📈 The integral of x * e^x is found by setting x as 'u' and e^x dx as 'dv', resulting in x * e^x - e^x + C.
- 🌀 For integrals involving trigonometric functions, such as x * sin(x), setting x as 'u' and sin(x) dx as 'dv' leads to -x * cos(x) + sin(x) + C.
- 📘 When integrating a product of a polynomial and a logarithmic function, like x^2 * ln(x), it's often necessary to apply integration by parts multiple times.
- ⚡ The integral of ln(x) is x * ln(x) - x + C, which is derived using integration by parts and recognizing the integral of 1 dx as x.
- 🔗 The integral of x^2 * sin(x) involves using integration by parts twice and results in a complex expression involving both sine and cosine functions.
- 🌟 The integral of x^2 * e^x requires applying integration by parts twice, leading to a solution involving powers of e^x.
- 📉 The integral of ln(x) squared involves rewriting the expression and applying integration by parts, resulting in x * ln(x) squared - 2x * ln(x) + 2x + C.
- 📊 The integral of ln(x) to the seventh power is simplified by recognizing it as 7 * ln(x), leading to 7 * (x * ln(x) - x) + C.
- 🌌 The integral of e^x * sin(x) is solved by recognizing the pattern in the integral and using a clever manipulation to find the solution as (1/2) * e^x * (sin(x) - cos(x)) + C.
Q & A
What is the integral of x times e^x?
-The integral of x times e^x is found using integration by parts, setting u=x and dv=e^x dx, which gives du=dx and v=e^x. The result is x * e^x - integral of e^x dx, which simplifies to x * e^x - e^x + C, where C is the constant of integration.
How do you integrate x times sine x dx?
-For x times sine x, set u=x and dv=sine x dx, giving du=dx and v=-cosine x. Using integration by parts, the integral becomes -x * cosine x + integral of cosine x dx, which simplifies to -x * cosine x + sine x + C.
What is the antiderivative of x squared times ln x?
-To find the antiderivative of x squared times ln x, set dv=x squared dx and u=ln x, giving v=x cubed / 3 and du=1/x dx. The integral by parts results in (1/3) * x cubed * ln x - (1/3) * integral of x squared dx, which simplifies to (1/3) * x cubed * ln x - (1/9) * x cubed + C.
How can you find the integral of the natural log of x using integration by parts?
-For the natural log of x, set u=ln x and dv=dx, giving du=1/x dx and v=x. The integral by parts formula yields x * ln x - integral of x * (1/x) dx, which simplifies to x * ln x - x + C.
What is the indefinite integral of x squared times sine x dx?
-For x squared times sine x, you need to use integration by parts twice. Initially, set u=x squared and dv=sine x dx, giving du=2x dx and v=-cosine x. The process involves further integration by parts on the resulting integral of 2x * cosine x dx, leading to a final answer involving x squared * cosine x, 2x * sine x, and 2 * cosine x, plus the constant C.
How do you integrate x squared times e^x dx?
-For x squared times e^x, use integration by parts twice. Start by setting u=x squared and dv=e^x dx, giving du=2x dx and v=e^x. The process involves another round of integration by parts with u=2x and dv=e^x dx, leading to a final expression involving e^x terms and a constant C.
What is the integral of ln x squared dx?
-To integrate ln x squared, set u=ln x squared and dv=dx, giving du=2 * ln x * (1/x) dx and v=x. The integral by parts results in x * ln x squared - 2 integral of ln x * (1/x) dx. Solving this requires recognizing the integral of ln x and simplifying to get the final answer involving x * ln x squared, -2x * ln x, and 2x, plus C.
How can you rewrite the integral of ln x to the seventh power dx?
-The integral of ln x to the seventh power can be rewritten using the property of logs to move the exponent to the front, resulting in 7 * integral of ln x dx. Since the integral of ln x is x * ln x - x, the final answer is 7 * (x * ln x - x) + C.
What is the indefinite integral of e^x times sine x dx?
-For e^x times sine x, set u=sine x and dv=e^x dx, giving du=cosine x dx and v=e^x. Using integration by parts, the process involves recognizing the similarity of the resulting terms to the original integral and solving for the integral, leading to a final answer involving e^x * (sine x - cosine x) / 2 plus C.
How do you find the antiderivative of ln x squared divided by x dx?
-To find the antiderivative of ln x squared / x, rewrite it as ln x squared * 1/x dx and use integration by parts with u=ln x squared and dv=1/x dx, giving du=2 * ln x * (1/x) dx and v=ln x. The process involves recognizing the similarity of terms and solving for the integral, resulting in ln x cubed / 3 plus C.
What is the indefinite integral of e^(3x) times cosine 4x dx?
-For e^(3x) times cosine 4x, set u=cosine 4x and dv=e^(3x) dx, giving du=-sine 4x * 4 dx and v=(1/3)e^(3x). Using integration by parts, the process involves moving constants to the front and recognizing the similarity of terms, leading to a final answer involving e^(3x) * (cosine 4x / 3 + 4/3 * sine 4x) plus C.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

LENGKAP Integral tak tentu, integral tertentu, integral subtitusi dan integral parsial

Cara Cepat Integral Parsial Aljabar [LENGKAP] - Matematika Peminatan Kelas 12 - Part 5
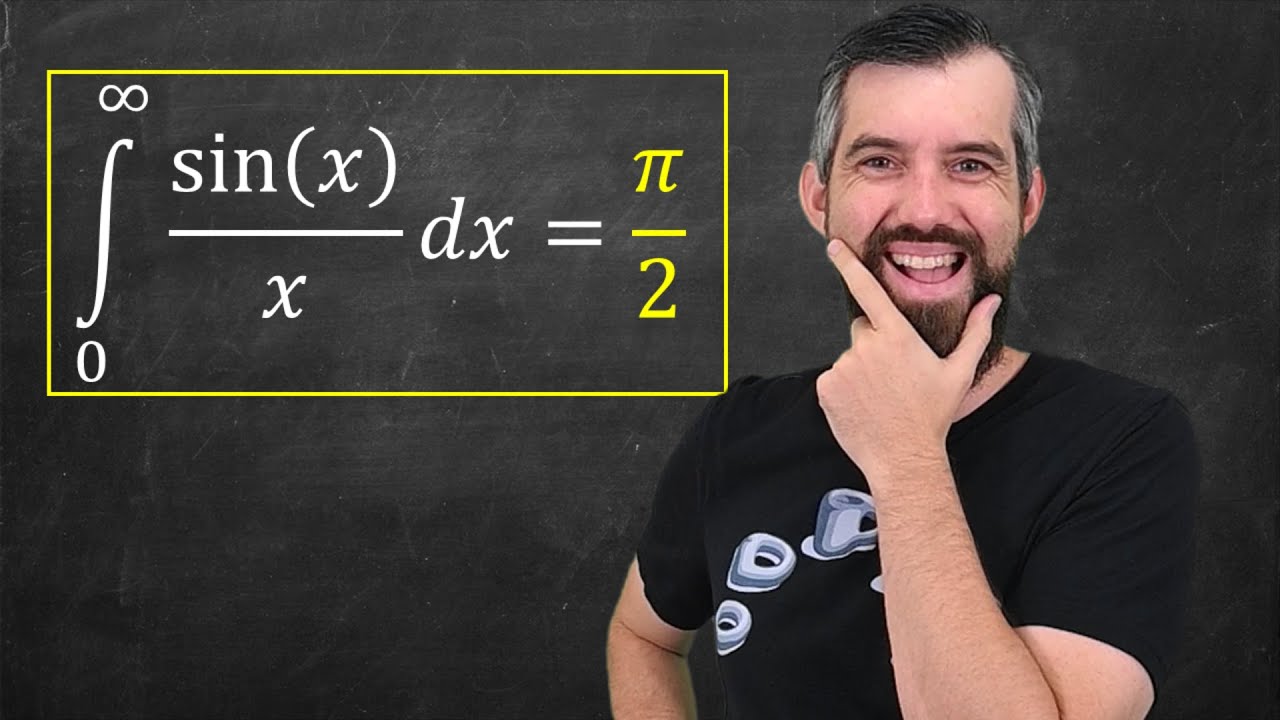
The Dirichlet Integral is destroyed by Feynman's Trick

FOURIER SERIES SOLVED PROBLEM 1 (LECTURE 9) @TIKLESACADEMY

BELAJAR INTEGRAL DARI DASAR DALAM 12 MENIT!

KALKULUS | TEKNIK PENGINTEGRALAN | METODE INTEGRAL PARSIAL
5.0 / 5 (0 votes)
