Statistics for Psychology

Summary

This video script offers an informative overview of the normal distribution, a fundamental concept in statistics. It explains the characteristics of a normal distribution curve, including symmetry, the mean, median, and mode aligning at the center, and its asymptotic nature. The script delves into the significance of the mean and standard deviation, illustrating how they define the spread of data points. It also covers the '68-95-99.7' empirical rule, which quantifies the proportion of data within one, two, or three standard deviations from the mean. The presenter uses the example of gummy bear consumption to demonstrate how to calculate and interpret z-scores, providing a practical application of normal distribution in real-world scenarios.

Takeaways

• 📚 The normal distribution is a fundamental concept in statistics, characterized by its bell shape and symmetry.
• 🔍 The mean, median, and mode of a normal distribution all coincide at the center of the distribution curve.
• 📉 The normal distribution is asymptotic, meaning it extends indefinitely in both directions without ever reaching zero.
• 🌐 The distribution is useful for modeling real-world phenomena because it captures the majority of data within a few standard deviations from the mean.
• 📈 The probability of data points falling within one standard deviation from the mean is approximately 68%, two standard deviations capture about 95%, and three standard deviations nearly 100%.
• 📊 Normal distributions can vary in their means and standard deviations, but the key property of capturing a certain percentage of data within specific standard deviations remains consistent.
• 🔢 The mean represents the average value, while the standard deviation measures the spread or dispersion of the data around the mean.
• 🤔 Understanding the standard deviation helps in gauging how typical a data point is; for example, a person eating 100 pounds of gummy bears per day with a standard deviation of 10 would be considered normal.
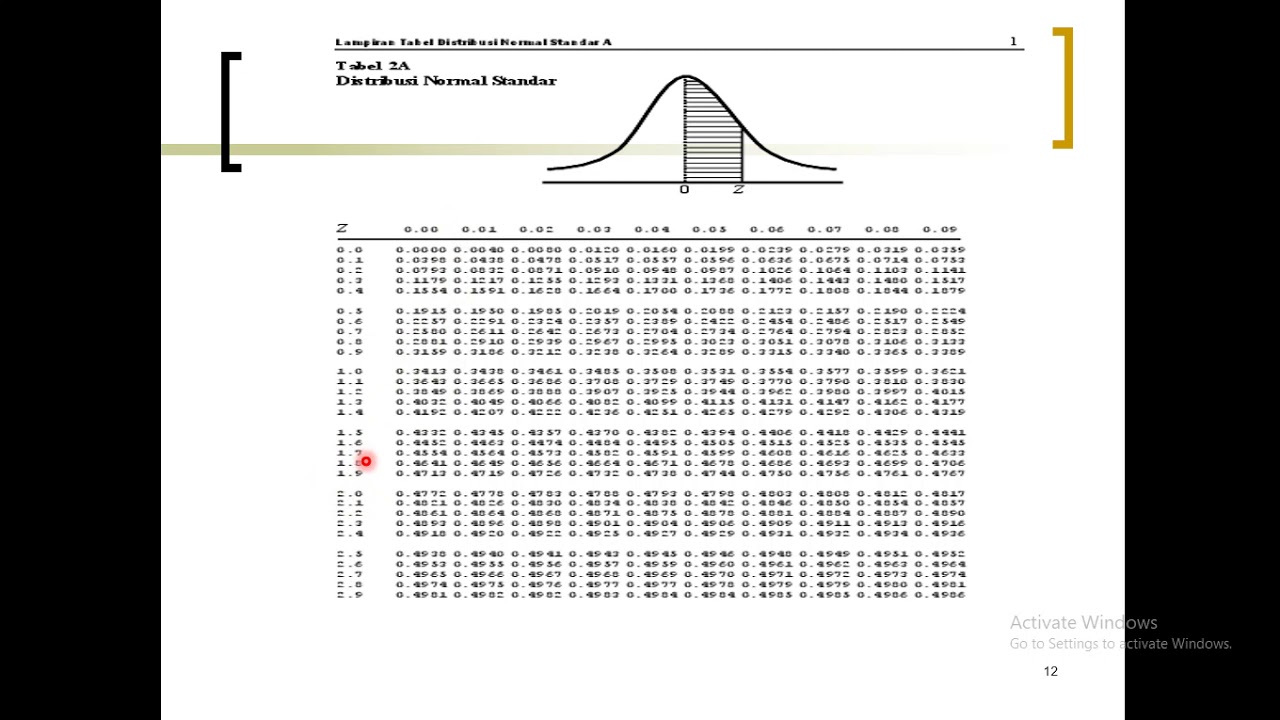
• 📚 To work with different normal distributions, z-scores are used to standardize the data, making it easier to compare and interpret using a single table.
• ➗ The z-score is calculated by subtracting the mean from the data point and then dividing by the standard deviation, indicating how many standard deviations away from the mean the data point lies.
• 🔎 By using z-scores and referring to a standard normal distribution table, one can determine the probability of a data point occurring beyond a certain threshold, like the likelihood of someone eating more than 140 pounds of gummy bears per day.

Q & A

What is the shape of a normal distribution curve?

The normal distribution curve is bell-shaped, symmetrical around its mean, with the mean, median, and mode all coinciding at the center of the curve.

Why is the normal distribution considered to be asymptotic?

The normal distribution is considered asymptotic because it theoretically extends indefinitely in both directions without ever reaching zero, although for practical purposes, it captures nearly all data within a few standard deviations from the mean.

What is the significance of the mean, median, and mode being equal in a normal distribution?

The equality of the mean, median, and mode in a normal distribution signifies that the data is perfectly symmetrical, and the central tendency measures are consistent, reflecting a balanced distribution of data points around the center.

How does the normal distribution help in modeling real-world phenomena?

The normal distribution is useful for modeling real-world phenomena because it captures the central limit theorem, where the sum of a large number of independent and identically distributed variables tends to form a normal distribution, making it a common statistical model for various natural and social phenomena.

What is the Empirical Rule in relation to the normal distribution?

The Empirical Rule states that for a normal distribution, approximately 68% of the data falls within one standard deviation of the mean, 95% within two standard deviations, and 99.7% within three standard deviations.

What is a z-score and how is it calculated?

A z-score is a measure of how many standard deviations an element is from the mean in a normal distribution. It is calculated by subtracting the mean from the data point and then dividing by the standard deviation.

Why is standardizing scores into z-scores useful in statistics?

Standardizing scores into z-scores is useful because it allows for easy comparison of data across different normal distributions, as it transforms the data into a common scale where the mean is 0 and the standard deviation is 1, facilitating the use of standard tables for probability calculations.

What is the relationship between a z-score and the probability of a data point occurring?

The z-score indicates the number of standard deviations a data point is from the mean, and by looking up the z-score in a standard normal distribution table, one can determine the probability or percentage of data points occurring at that distance from the mean.

How can you find the probability of a data point being beyond a certain value in a normal distribution?

To find the probability of a data point being beyond a certain value, calculate the z-score for that value, look up the corresponding area in a standard normal distribution table, and then subtract this area from 0.5 if you want the probability beyond that value in one tail, or from 1 if considering both tails.

What is an example of a practical scenario where the normal distribution is applied as described in the script?

An example given in the script is determining the likelihood of a person eating more than 140 pounds of gummy bears per day, assuming the average consumption is 100 pounds with a standard deviation of 10, by calculating the z-score for 140 and using a standard normal distribution table to find the probability.

How does the script illustrate the concept of 'freakishly high' or 'freakishly low' in the context of the normal distribution?

The script uses the phrase 'freakishly high' or 'freakishly low' to describe data points that are more than one standard deviation above or below the mean, indicating that these occurrences are less common and deviate significantly from the norm.