Z-Scores, Standardization, and the Standard Normal Distribution (5.3)

Summary

This video script offers an insightful exploration of z-scores and the standardization process in statistics. It explains the concept of the standard normal distribution, a bell curve with a mean of 0 and a standard deviation of 1. The script delves into how to calculate exact proportions using this distribution and z-score tables, illustrating the process with examples. It also highlights the benefits of standardization, allowing for the conversion of any normal distribution into the standard form, and demonstrates how to apply this to calculate specific areas under the curve, providing a practical understanding of statistical analysis.

Takeaways

• 📊 The standard normal distribution is a type of normal distribution with a mean of 0 and a standard deviation of 1.
• 🧮 A z-score represents how many standard deviations an observation is from the mean.
• 📉 A negative z-score indicates that the observation is below the mean, while a positive z-score indicates it's above the mean.
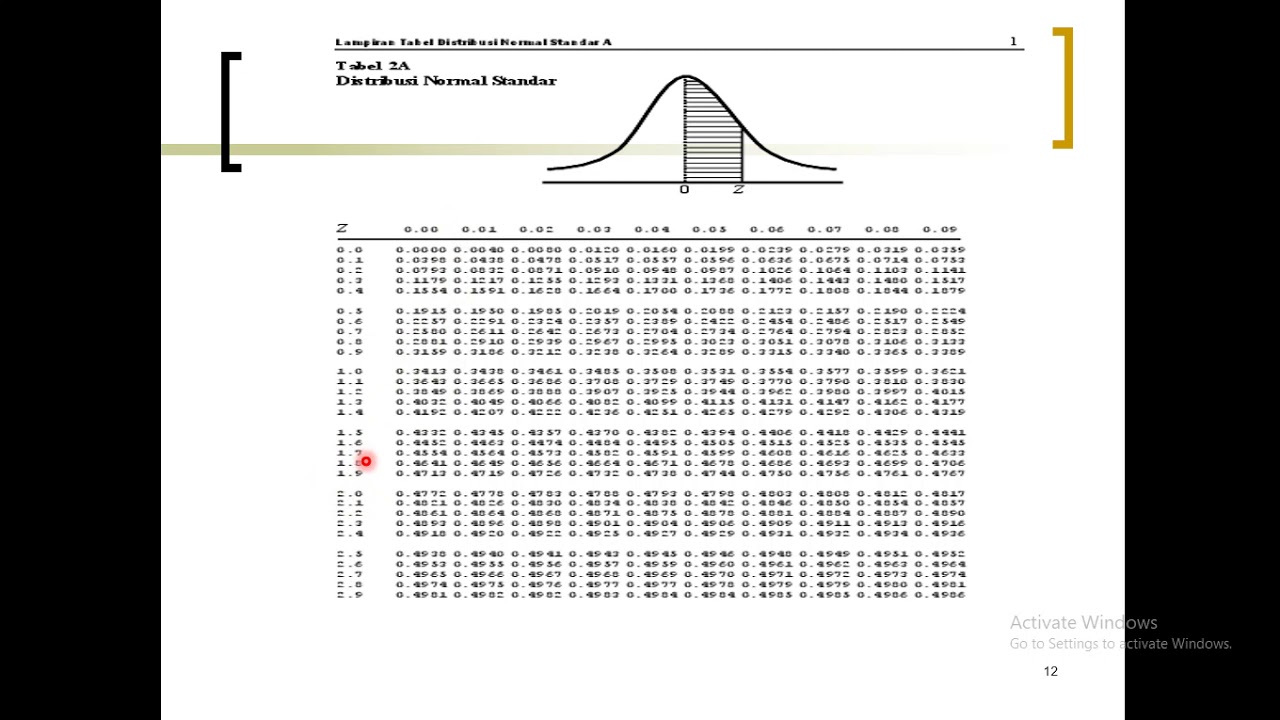
• 📑 The z-score table (standard normal table) helps to calculate the area (proportion) to the left of any z-score.
• 🔄 To find the area to the right of a z-score, subtract the table value from 1.
• 🔍 The z-score table can also be used for reverse look-ups to find the z-score associated with a specific area.
• 🔄 Any normal distribution can be standardized, converting it to a standard normal distribution with a mean of 0 and a standard deviation of 1.
• 🧪 The formula for standardization is z = (X - μ) / σ, where X is the observation, μ is the mean, and σ is the standard deviation.
• 📏 Standardization allows you to use the z-score table to calculate areas for any normally distributed population.
• 📐 The proportion of values within a specific range can be calculated by finding the z-scores of the range limits and then subtracting the corresponding areas.

Q & A

What is a standard normal distribution?

A standard normal distribution is a special type of normal distribution with a mean of 0 and a standard deviation of 1. It is always centered at 0, and each number on the horizontal axis corresponds to a z-score, which indicates how many standard deviations an observation is from the mean.

What does a z-score represent?

A z-score represents the number of standard deviations an observation is from the mean (mu). For example, a z-score of -2 indicates that the observation is 2 standard deviations below the mean, while a z-score of 1.5 indicates it is 1.5 standard deviations above the mean.

How can we find the exact area associated with a specific z-score?

We can find the exact area associated with a specific z-score using a z-score table, also known as the standard normal table. This table provides the total amount of area contained to the left side of any z-value.

What is the proportion of Z less than -1.95 according to the standard normal table?

According to the standard normal table, the proportion of Z less than -1.95 is 0.0256. This means there is 2.56% of the area to the left of a z-score of -1.95.

How do we determine the area to the right of a z-score?

To determine the area to the right of a z-score, we find the area that corresponds to that z-value in the standard normal table and then subtract it from 1. For example, to find the area to the right of a z-score of 0.57, we subtract the area of 0.7157 (to the left of 0.57) from 1, resulting in an area of 0.2843.

What is the purpose of using a z-score table for reverse look-up?

The purpose of using a z-score table for reverse look-up is to determine what z-score corresponds to a specific area. For instance, if you want to know what z-score is associated with an area of 0.8446 to the left of it, you find 0.8446 on the table and see the corresponding z-score, which is 1.02.

What is the process of standardization in the context of normal distributions?

Standardization is the process of converting any normal distribution with any mean (mu) and standard deviation (sigma) into the standard normal distribution, where the mean is zero and the standard deviation is one. This allows the use of the z-score table to calculate exact areas for any given normally distributed population.

What is the standardization formula used to convert a normal distribution to a standard normal distribution?

The standardization formula is Z = (X - mu) / sigma, where Z is the z-score, X is the observation, mu is the population mean, and sigma is the population standard deviation.

How can we find the proportion of students scoring less than 49 on an exam with a mean of 60 and a standard deviation of 10?

First, we standardize the distribution using the formula Z = (X - mu) / sigma. For X = 49, the z-score is -1.1. Then, we look up the z-score of -1.1 in the standard normal table to find the proportion of Z less than -1.1, which is 0.1357. This is the proportion of students scoring less than 49.

What proportion of students are between 5.81 feet and 6.3 feet tall if the height distribution has a mean of 5.5 feet and a standard deviation of 0.5 feet?

We standardize the distribution to find the z-scores for 5.81 feet (z = 0.62) and 6.3 feet (z = 1.6). Then, we subtract the area corresponding to z = 0.62 (0.7304) from the area corresponding to z = 1.6 (0.9452), resulting in a proportion of 0.2148, or 21.48% of students.

Outlines

00:00

📚 Introduction to Z-Scores and Standard Normal Distribution

This paragraph introduces the concept of Z-scores and the standard normal distribution. It explains that the standard normal distribution is a special kind of normal distribution with a mean of 0 and a standard deviation of 1, making it symmetrical and centered at zero. The paragraph details how Z-scores indicate the number of standard deviations an observation is from the mean, with examples provided to illustrate this. It also discusses the use of the Z-score table, or the standard normal table, to find the exact area associated with a specific Z-score, and how to use this table to determine areas to the left or right of any Z value. The process of standardization is introduced as a method to convert any normal distribution into the standard normal distribution, using a specific formula that involves subtracting the population mean and dividing by the population standard deviation. An example using final chemistry exam scores is given to demonstrate how to use the standardization formula and Z-score table to find the proportion of students scoring below a certain threshold.

05:02

📏 Applying Standardization to Measure Heights and Calculate Proportions

The second paragraph applies the concept of standardization to a real-world example of measuring the heights of university students, which are normally distributed with a mean of 5.5 feet and a standard deviation of 0.5 feet. The paragraph outlines the process of using the standardization formula to convert individual height measurements into Z-scores, which allows for the use of the standard normal table to find the corresponding areas. The example calculates the proportion of students with heights between 5.81 feet and 6.3 feet by finding the Z-scores for these heights, looking up the areas in the standard normal table, and subtracting the smaller area from the larger one to find the difference. The result is a proportion of students within the specified height range, demonstrating the practical application of Z-scores and standardization in statistical analysis.

Keywords

💡Z-scores

Z-scores, also known as standard scores, measure the number of standard deviations an element is from the mean in a normal distribution. In the context of the video, Z-scores are crucial for understanding how data points relate to the mean and standard deviation of a distribution, particularly the standard normal distribution with a mean of 0 and a standard deviation of 1. For example, a Z-score of -2 indicates that a data point is two standard deviations below the mean.

💡Standard Normal Distribution

The standard normal distribution is a specific type of normal distribution that has a mean (μ) of 0 and a standard deviation (σ) of 1. This distribution is central to the video's theme as it serves as a reference for converting any normal distribution into a form where data can be easily compared and analyzed using Z-scores. The video explains that any normal distribution can be standardized to this form, allowing for the use of Z-scores to calculate exact proportions.

💡Mean (μ)

The mean, often denoted by the Greek letter μ, is the average value of a data set. In the video, the mean is used to describe the central location of a normal distribution. For instance, when discussing the final chemistry exam data, the mean score of 60 is the reference point for calculating Z-scores and determining how students' scores deviate from the average.

💡Standard Deviation (σ)

Standard deviation, represented by σ, is a measure of the amount of variation or dispersion in a set of values. In the video, the standard deviation is essential for standardizing a normal distribution and calculating Z-scores. It helps determine how spread out the data is from the mean, with larger standard deviations indicating greater variability.

💡Z-score Table

A Z-score table, also known as the standard normal table, is used to find the cumulative area under the standard normal curve to the left of a given Z-score. The video emphasizes the importance of this table in determining the proportion of data that falls within a certain range, as it provides the exact area associated with a specific Z-score.

💡Proportion

Proportion in this video refers to the fraction or percentage of data points that fall within a specific range in a distribution. It is calculated using Z-scores and the standard normal table. For example, the video explains how to find the proportion of students scoring below a certain point on an exam by using the area associated with the corresponding Z-score.

💡Standardization

Standardization is the process of converting any normal distribution into the standard normal distribution. The video demonstrates how this is done using a formula that involves subtracting the mean and dividing by the standard deviation. This process is essential for using Z-scores to compare and analyze data across different normal distributions.

💡Area Under the Curve

In the context of the video, the area under the curve refers to the proportion of data points within a certain range in a normal distribution. This is determined using the standard normal table and is crucial for understanding the distribution of data points relative to the mean. The video shows how to calculate this area for both tails and intervals of the standard normal distribution.

💡Observation (X)

An observation in the video represents an individual data point within a dataset. The process of standardization involves using the value of an observation (X) to calculate its corresponding Z-score, which then allows for the determination of its position relative to the mean and the standard deviation of the distribution.

💡Density Curve

A density curve, as mentioned in the video, is a graphical representation of a distribution where the total area under the curve equals 1 (or 100%). This is important for understanding the standard normal distribution, as it ensures that the total proportion of data points across all Z-scores adds up to the entire dataset.

💡Reverse Look-up

Reverse look-up in the video refers to the process of using the standard normal table to find the Z-score that corresponds to a specific area under the curve. This is the opposite of the more common use of the table to find the area associated with a given Z-score. The video illustrates how this can be used to determine the Z-score for a particular proportion of data points.

Highlights

The standard normal distribution is a unique normal distribution with a mean of 0 and a standard deviation of 1, allowing for easy calculation of exact proportions using the z-score.

Z-scores indicate the number of standard deviations an observation is from the mean, with negative values indicating below the mean and positive values above.

A z-score table, also known as the standard normal table, provides the total area to the left of any z-score, facilitating the calculation of exact areas.

The proportion of Z less than a specific value can be formally stated, for example, Z less than -1.95 corresponds to an area of 0.0256.

The area to the right of any z-score can be determined by subtracting the area to the left from 1, as demonstrated with a z-score of 0.57 leading to an area of 0.2843.

The z-score table can perform a reverse lookup to find the z-score associated with a specific area, such as finding the z-score for an area of 0.8416 to the left.

Any normal distribution can be transformed into the standard normal distribution through a process called standardization, which uses a specific formula.

Standardization benefits from the ability to use the z-score table to calculate exact areas for any given normally distributed population, regardless of the mean (mu) or standard deviation (sigma).

The standardization formula involves subtracting the population mean from an observation and dividing by the population standard deviation.

An example demonstrates converting a normal distribution of final chemistry exam scores with a mean of 60 and a standard deviation of 10 into the standard normal distribution.

The conversion process results in the mean being zero and the standard deviation being one, consistent with the standard normal distribution.

Using the standardization formula, one can determine the proportion of students scoring below a certain value, such as less than 49 on an exam.

The proportion of students scoring below 49 is found to be 0.1357, using the z-score table for a z-score of -1.1.

Another example involves determining the proportion of students with heights between 5.81 and 6.3 feet, using the standardization formula with a mean height of 5.5 feet and a standard deviation of 0.5 feet.

The proportion of students within the specified height range is calculated to be 0.2128 by subtracting the areas corresponding to z-scores of 0.62 and 1.6.

Support for the video creators can be provided through Patreon, and additional study materials can be accessed on their website, Simple Learning Pro.

Transcripts

in this video we'll be learning about

zet scores and standardization by

learning about both of these topics you

will learn how to calculate exact

proportions using the standard normal

distribution what is the standard normal

distribution the standard normal

distribution is a special type of normal

distribution that has a mean of 0 and a

standard deviation of 1 because of this

the standard normal distribution is

always centered at 0 and has intervals

that increase by 1 each number on the

horizontal axis corresponds to a z-score

as zetz core tells us how many standard

deviations an observation is from the

mean mu for example a z-score of

negative 2 tells me that I am 2 standard

deviations to the left of the mean and

as that score of 1.5 tells me that I am

one and a half standard deviations to

the right of the mean most importantly a

set score allows us to calculate how

much area that specific z-score is

associated with and we can find out that

exact area using something called a

z-score table also known as the standard

normal table this table tells us the

total amount of area contained to the

left side of any value of Z for this

table the top row and the first column

correspond to Z values and all the

numbers in the middle correspond to

areas for example according to the table

a z-score of negative 1 point 9 5 has an

area of 0.025 6 to the left of it to say

this in a more formal manner we can say

that the proportion of Z less than

negative one point nine five is equal to

0.025 6 we can also use the standard

normal table to determine the area to

the right of any Z value all we have to

do is take 1 minus the area that

corresponds to that value for example to

determine the area to the right of a

z-score of 0.57 all we have to do is

find the area that corresponds to this

set value and then subtracted from 1

according to the table the z-score of

0.57 has an area of 0.7 157 to the left

of it so 1 minus 0.7 157 gives us an

area of 0.28 43 and that is our answer

the reason why we can do this is because

we have to remember that the normal

distribution is a density curve and it

always has a total area equal to 1 or

percent you can also use the set score

table to do a reverse look-up which

means you can use the table to see what

that score is associated with a specific

area so if I wanted to know what value

of Zed corresponds to an area of 0.8

four six one to the left of it

all we have to do is find zero point

eight four six one on the table and see

what value is that it corresponds to we

see that it corresponds to a set value

of one point zero two the special thing

about the standard normal distribution

is that any type of normal distribution

can be transformed into it in other

words any normal distribution with any

value of mu and Sigma can be transformed

into the standard normal distribution

where you have a mean of zero and a

standard deviation of one this

conversion process is called

standardization the benefit of

standardization is that it allows us to

use the set score table to calculate

exact areas for any given normally

distributed population with any value of

mu or Sigma standardization involves

using this formula this formula says

that the z-score is equal to an

observation X minus the population mean

mu divided by the population standard

deviation Sigma so suppose that we

gather data from last year's final

chemistry exam and found that it

followed a normal distribution with a

mean of 60 and a standard deviation of

10 if we were to draw this normal

distribution we would have 60 located at

the center of the distribution because

it is the value of the mean and each

interval would increase by 10 since that

is the value of the standard deviation

to convert this distribution to the

standard normal distribution we will use

the formula the value of MU is equal to

60 and the value of Sigma is equal to 10

we can then take each value of x and

plug it into the equation if I plug in

60 I will get a value of 0 if I plug in

50 I will get a value of negative 1 if I

plug in 40 I will get a value of

negative 2 if we do this for each value

you can see that we end up with the same

values as a standard normal distribution

when doing this conversion process the

mean of the normal distribution will

always be converted to zero and the

standard deviation will always

correspond to a value of 1 it's

important to remember that this will

happen with any normal distribution no

matter what value of MU and sick

are now if I asked you what proportion

of students score less than 49 on the

exam it is this area that we are

interested in however the proportion of

X less than 49 is unknown until we use

the standardization formula after

plugging in 49 into this formula we end

up with a value of negative 1.1 as a

result we will be looking for the

proportion of Zed less than negative 1.1

and finally we can use the z-score table

to determine how much area is associated

with his Zed score according to the

table there's an area of 0.1 3 5 7 to

the left of this set value this means

that the proportion of Zed less than

negative 1.1 is zero point 1 3 5 7 this

value is in fact the same proportion of

individuals that scored less than 49 on

the exam as a result this is the answer

let's do one more example when measuring

the heights of all students at a local

university it was found that it was

normally distributed with a mean height

of 5.5 feet and a standard deviation of

0.5 feet what proportion of students are

between five point eight one feet and

6.3 feet tall before we solve this

question it's always a good habit to

first write down important information

so we have a meal of 5.5 feet and a

sigma of 0.5 feet we are also looking

for the proportion of individuals

between 5.8 one feet and 6.3 feet tall

this corresponds to this highlighted

area to determine this area we need to

standardize the distribution so we will

use the standardization formula plugging

in 5.8 went to this formula gives us a

Zed square of 0.62 and plugging in 6.3

into the formula gives us a z-score of

1.6

according to the standard normal table

the z-score of 0.62 corresponds to an

area of 0.7 3 to 4 and the z-score of

1.6 corresponds to an area of 0.945 2 to

find the proportion of values between

0.62 and 1.6 we must subtract the

smaller area from the bigger area so

0.945 2 minus 0.7 3 to 4 gives us zero

point 2 1 to 8 as a result the

proportion of students between 5.8 one

feet and 6.3 feet tall is zero point two

one two eight if you found this video

helpful

consider supporting us on patreon to

help us make more videos you can also

visit our website at simple learning

procom to get access to many study

guides and practice questions thanks for

watching