Bayesian Estimation in Machine Learning - Maximum Likelihood and Maximum a Posteriori Estimators
Summary
TLDRThis video script delves into maximum likelihood estimation (MLE), least squares, and machine learning model training. It explains how MLE and least squares minimize the error between observed and modeled data. The speaker also discusses the role of priors in maximum a posteriori estimation (MAP), as well as the impact of measurement and model errors. The script transitions into machine learning, comparing MLE and MAP in training neural networks for regression and classification tasks. Finally, it emphasizes the importance of assumptions about data distributions and how deviations can affect model performance.
Takeaways
- 😀 The goal is to minimize the difference between observed data (Y) and the modeled data (K * X), which is essentially a least squares problem.
- 😀 The least squares method is optimal when maximizing the likelihood of the data, assuming a Gaussian distribution for noise.
- 😀 Likelihood represents the probability of observing the data Y, given a model and signal X.
- 😀 The noise in the measurement is modeled as Gaussian, which leads to a likelihood modeled by a multivariate Gaussian distribution.
- 😀 The maximum likelihood estimation (MLE) maximizes the probability of observing the data, which simplifies to least squares under the assumption of Gaussian noise.
- 😀 Posterior estimation in Bayesian inference maximizes the probability of X given the observation Y and model, incorporating both likelihood and prior distributions.
- 😀 Bayes' theorem allows the joint probability to be split into the product of likelihood and prior probability, leading to posterior estimation.
- 😀 The maximum a posteriori (MAP) estimator incorporates a prior distribution for X and leads to a regularization term (like L2 norm regularization).
- 😀 The MAP estimator depends on the prior distribution of X and the likelihood model, and can be used to derive regularization methods such as Tikhonov regularization.
- 😀 For machine learning, the model parameters are trained first, and the prediction of X depends on both model error and measurement error.
- 😀 Maximum likelihood estimation in machine learning involves maximizing the likelihood of training data, while also considering prior assumptions about the model parameters.
- 😀 For regression problems, the MLE typically involves minimizing L2 loss, while for classification problems, it involves minimizing cross-entropy loss based on predicted probabilities.
- 😀 The MLE and MAP estimators depend on the assumptions about data distributions (e.g., Gaussian for regression, multinomial for classification) and violations of these assumptions can degrade performance.
Q & A
What is the primary objective of the script?
-The primary objective is to explain the concepts of maximum likelihood estimation (MLE) and maximum a posteriori estimation (MAP), showing how they are used in deterministic models and machine learning contexts.
How does the least squares method relate to MLE?
-The least squares method is shown to be equivalent to maximum likelihood estimation (MLE) under the assumption that the measurement noise follows a Gaussian distribution. Minimizing the squared difference between observed and modeled values leads to the MLE.
What is the likelihood function, and how is it used in MLE?
-The likelihood function represents the probability of observing the data given a certain model and parameters. In MLE, this likelihood function is maximized to estimate the model parameters that best explain the observed data.
What does the Base Theorem say in the context of Bayesian estimation?
-Bayes' Theorem in this context states that the joint probability of two events can be expressed as the product of the likelihood and the prior probability. It allows the calculation of the posterior distribution, which is used to estimate the parameters of interest.
What is the role of the prior distribution in MAP estimation?
-In MAP estimation, the prior distribution represents prior knowledge or beliefs about the parameters before observing the data. The posterior distribution is then maximized, incorporating both the likelihood of the data and the prior distribution.
How does regularization affect MAP estimation?
-Regularization in MAP estimation introduces a penalty term (often based on L2 norms) to prevent overfitting by discouraging overly complex parameter estimates. This results in a more stable and generalizable model.
What is the difference between deterministic models and machine learning models in the context of parameter estimation?
-In deterministic models, the parameters are directly estimated through MLE or MAP without the need for training. In machine learning models, the parameters (such as weights in neural networks) are learned through a training process, and the uncertainty in prediction depends on model error and measurement error.
What does the error covariance matrix represent in Bayesian estimation?
-The error covariance matrix represents the uncertainty in the parameter estimates. It combines the uncertainty due to measurement noise and the prior knowledge of the parameters, and it quantifies the spread or variability of the estimated parameters.
What assumption is made about the prior distribution in Bayesian estimation for deterministic models?
-The prior distribution in Bayesian estimation for deterministic models is assumed to follow a multivariate Gaussian distribution with a specific mean (the expectation of X) and covariance matrix, which is a common assumption in many practical scenarios.
How does the MLE approach apply differently to regression and classification problems?
-For regression problems, MLE typically minimizes the L2 loss, which is the squared difference between predicted and actual values. For classification problems, MLE minimizes the cross-entropy loss, which involves comparing the predicted probabilities to the true class labels.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Presentation16: Using Maximum Likelihood Estimation to Calibrate a Discrete Time Markov Model
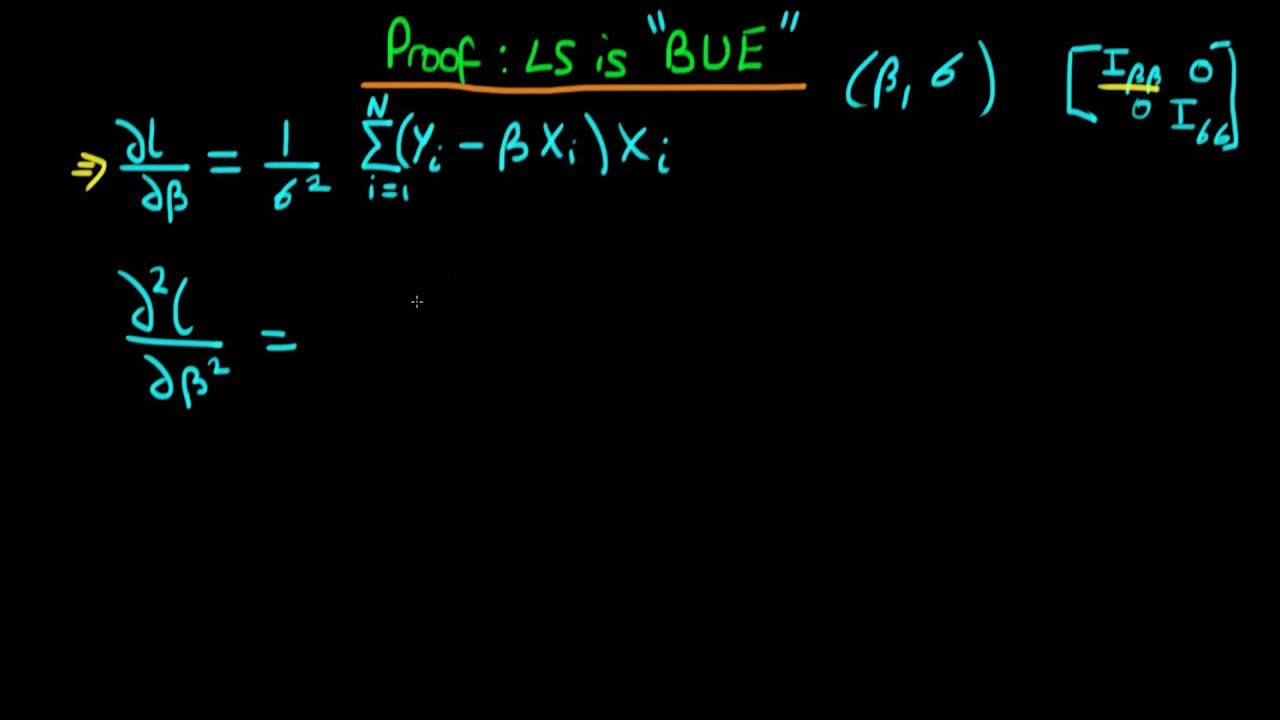
Least squares comparison with Maximum Likelihood - proof that OLS is BUE

Applying MLE for estimating the variance of a time series
StatQuest: Logistic Regression
Maximum Likelihood, clearly explained!!!

What are Maximum Likelihood (ML) and Maximum a posteriori (MAP)? ("Best explanation on YouTube")
5.0 / 5 (0 votes)
