Presentation16: Using Maximum Likelihood Estimation to Calibrate a Discrete Time Markov Model
Summary
TLDRThis video lesson explores the use of maximum likelihood estimation (MLE) to calibrate a discrete time Markov model for studying vegetation succession in desert plant communities. It details the process of collecting time series data to estimate transition probabilities, forming a likelihood function from observed state transitions, and calculating MLE using transition counts. The importance of pooling data from multiple independent observation sites to improve estimation accuracy is emphasized. Finally, the lesson highlights the applicability of these techniques to various systems adhering to the Markov property, providing valuable insights into ecological modeling.
Takeaways
- 😀 MLE is used to estimate transition probabilities in a discrete-time Markov model for vegetation succession.
- 😀 The Markov property states that future states depend only on the current state, not on past states.
- 😀 A likelihood function can be constructed from observed time series data to estimate transition probabilities.
- 😀 Transition counts (n_ij) are essential for forming the likelihood function and estimating transition probabilities.
- 😀 The formula for maximum likelihood estimates involves dividing transition counts by the total counts from the initial state.
- 😀 Collecting data from multiple independent observation sites can significantly improve the accuracy of transition estimates.
- 😀 Using a larger number of shorter time series observations is more efficient than a single long-term observation.
- 😀 The video emphasizes that improved data collection leads to better parameter estimates in Markov models.
- 😀 The true transition probabilities can be compared against estimates to assess accuracy and guide future data collection efforts.
- 😀 The findings can be generalized to other systems that exhibit Markov properties beyond desert plant communities.
Q & A
What is the main objective of the video lesson?
-The main objective is to demonstrate how to use maximum likelihood estimation to calibrate a discrete-time Markov model, specifically for studying vegetation succession dynamics in a desert plant community.
What are the nine transition probability parameters in the context of a Markov model?
-The nine parameters correspond to the probabilities of transitioning between different states, denoted as p11, p12, p13, etc., which represent the likelihood of moving from one state to another in the transition matrix.
How is the likelihood function for a time series constructed?
-The likelihood function is constructed by forming a product of transition probabilities for each observed state transition in the time series, based on the counts of transitions from state j to state i.
What is the significance of transition counts (n_ij)?
-Transition counts (n_ij) indicate the number of times a transition occurs from state j to state i in the observed time series, which are essential for estimating the transition probabilities.
How can the accuracy of transition probability estimates be improved?
-The accuracy can be improved by collecting data from multiple independent observation sites rather than relying on a single site, which allows for a larger dataset in a shorter time frame.
What are the two properties of a stationary discrete-time Markov model?
-The two properties are that the probability of transitioning to a future state depends only on the current state (Markov property) and that these probabilities do not change over time.
What is the maximum likelihood estimation formula for the transition probabilities?
-The formula states that the transition probability p_ij is estimated by dividing the corresponding transition count n_ij by the total transition counts starting from state j.
What does pooling transition counts involve, and why is it important?
-Pooling transition counts involves summing the transition counts across multiple observation sites, which provides a more accurate estimate of transition probabilities due to a larger sample size.
What results were observed when comparing estimated transition probabilities to true values?
-The estimated transition probabilities were found to be qualitatively similar to the true values but had some significant differences, indicating that the estimates could be improved with more data.
How does the approach of multiple observation sites enhance the study's feasibility?
-Using multiple sites allows researchers to gather substantial data over a shorter period, avoiding the impracticality of needing decades of single-site observations to achieve similar accuracy.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Bayesian Estimation in Machine Learning - Maximum Likelihood and Maximum a Posteriori Estimators

Applying MLE for estimating the variance of a time series
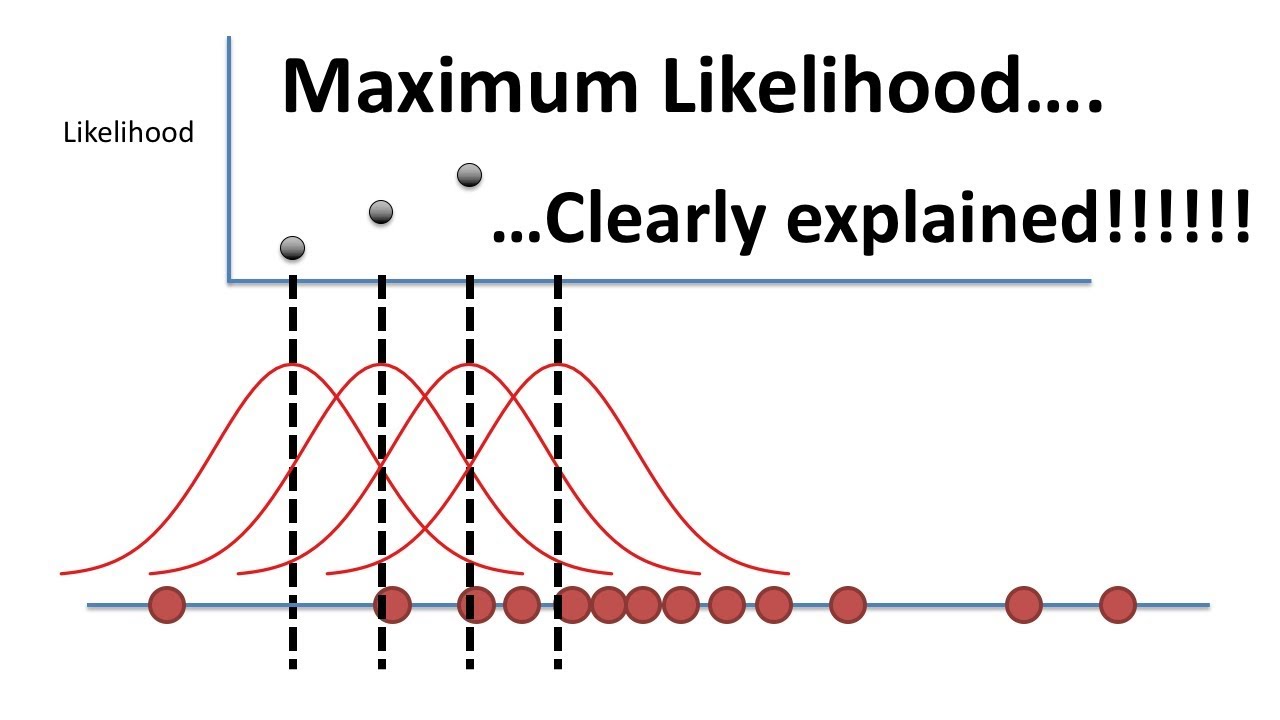
Maximum Likelihood, clearly explained!!!
Maximum Likelihood Estimation (Part 1)

What are Maximum Likelihood (ML) and Maximum a posteriori (MAP)? ("Best explanation on YouTube")

Lec-5: Logistic Regression with Simplest & Easiest Example | Machine Learning
5.0 / 5 (0 votes)