4 Métodos en 5 minutos para resolver sistema de ecuaciones lineales 2x2
Summary
TLDREste video presenta cuatro métodos para resolver un sistema de ecuaciones lineales 2x2: reducción, sustitución, igualación y la regla de Cramer. Se explica cómo aplicar cada método paso a paso, mostrando cómo despejar incógnitas, sustituir, igualar ecuaciones y usar matrices para calcular los determinantes. A lo largo de la explicación, se ilustra cómo llegar a la misma solución (x = 3, y = 1) utilizando diferentes enfoques. El video también menciona otros métodos como el gráfico y el de Gauss-Jordan, invitando a los espectadores a comentar cuál prefieren utilizar en sus ejercicios.
Takeaways
- 😀 El método de reducción, también conocido como suma y resta, se utiliza para resolver sistemas de ecuaciones lineales 2x2. El objetivo es cancelar términos semejantes y despejar las incógnitas.
- 😀 En el método de reducción, después de cancelar términos semejantes, se obtiene una solución para una incógnita, y luego se sustituye ese valor en la ecuación original para encontrar la otra incógnita.
- 😀 El método de sustitución implica despejar una incógnita en una de las ecuaciones, y luego sustituirla en la otra ecuación para resolver el sistema.
- 😀 En el método de sustitución, es importante reemplazar correctamente la expresión de la incógnita despejada en la otra ecuación para simplificar el sistema a una sola incógnita.
- 😀 El método de igualación consiste en despejar la misma incógnita en ambas ecuaciones y luego igualar ambas expresiones para obtener una ecuación con una sola incógnita.
- 😀 En el método de igualación, al despejar y igualar las incógnitas, se obtiene una ecuación simple que se resuelve de la misma manera que el método de sustitución.
- 😀 La regla de Cramer utiliza matrices para resolver sistemas de ecuaciones. Se calculan determinantes de matrices construidas con los coeficientes y los términos independientes.
- 😀 Para calcular la solución usando la regla de Cramer, se construyen dos matrices: una con los términos independientes y otra con los coeficientes de las incógnitas, luego se calculan sus determinantes.
- 😀 Es fundamental realizar una comprobación al final de cada método para asegurarse de que la solución es correcta. Esto puede implicar reemplazar las soluciones obtenidas en las ecuaciones originales.
- 😀 Además de los métodos mencionados, hay otros métodos como el gráfico y el de Gauss-Jordan que también pueden ser útiles para resolver sistemas de ecuaciones lineales.
Q & A
¿Qué es el método de reducción para resolver un sistema de ecuaciones lineales?
-El método de reducción, también conocido como el método de suma y resta, consiste en operar entre términos semejantes para eliminar una de las incógnitas, facilitando así la resolución del sistema. El objetivo es despejar una de las variables y luego sustituir el valor encontrado en la otra ecuación.
¿Cómo se encuentra el valor de 'x' usando el método de reducción?
-Se resuelve una de las ecuaciones de manera que una de las incógnitas se cancele al sumarlas o restarlas. Después de despejar una de las variables, se obtiene el valor de 'x' dividiendo los términos resultantes.
¿Qué pasos se siguen para encontrar el valor de 'y' después de hallar 'x' en el método de reducción?
-Una vez obtenido 'x', se sustituye en cualquiera de las dos ecuaciones originales. Se despeja 'y' y se realiza la operación correspondiente para obtener su valor.
¿En qué consiste el método de sustitución para resolver sistemas de ecuaciones?
-El método de sustitución consiste en despejar una incógnita en una de las ecuaciones, y luego sustituir esa expresión en la otra ecuación para resolverla. Esto permite reducir el sistema a una ecuación con una sola incógnita.
¿Qué significa la sustitución de 'x' en la segunda ecuación en el método de sustitución?
-Significa reemplazar la expresión despejada de 'x' en la segunda ecuación, lo que permite simplificar el sistema y resolverlo para la otra incógnita.
¿Cómo se resuelve el sistema después de sustituir 'x' en el método de sustitución?
-Se resuelve la ecuación resultante, despejando la incógnita restante (en este caso, 'y'). Luego, se obtiene el valor de 'y', y este valor se sustituye nuevamente en la ecuación original para encontrar 'x'.
¿En qué se diferencia el método de igualación del de sustitución?
-En el método de igualación, se despeja la misma incógnita en ambas ecuaciones y luego se igualan las expresiones obtenidas. Esto permite obtener una sola ecuación con una incógnita que se resuelve de manera similar al método de sustitución.
¿Cómo se resuelve un sistema usando el método de igualación?
-Después de igualar las expresiones despejadas de la misma incógnita, se resuelve la ecuación resultante para obtener el valor de una de las incógnitas. Posteriormente, este valor se sustituye en cualquiera de las ecuaciones originales para encontrar la otra incógnita.
¿Qué es la regla de Cramer y cómo se aplica en la resolución de sistemas de ecuaciones?
-La regla de Cramer es un método que utiliza matrices para resolver sistemas de ecuaciones lineales. Se construyen matrices para los coeficientes y términos independientes, y luego se calculan los determinantes de estas matrices para encontrar las soluciones del sistema.
¿Cómo se calculan los determinantes en la regla de Cramer para hallar 'x' y 'y'?
-Para calcular los determinantes, se multiplican los elementos de las diagonales de la matriz y luego se resta el producto de los elementos de la otra diagonal. El valor de 'x' se obtiene dividiendo el determinante de la matriz del numerador por el determinante de la matriz del denominador, y lo mismo se hace para 'y'.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
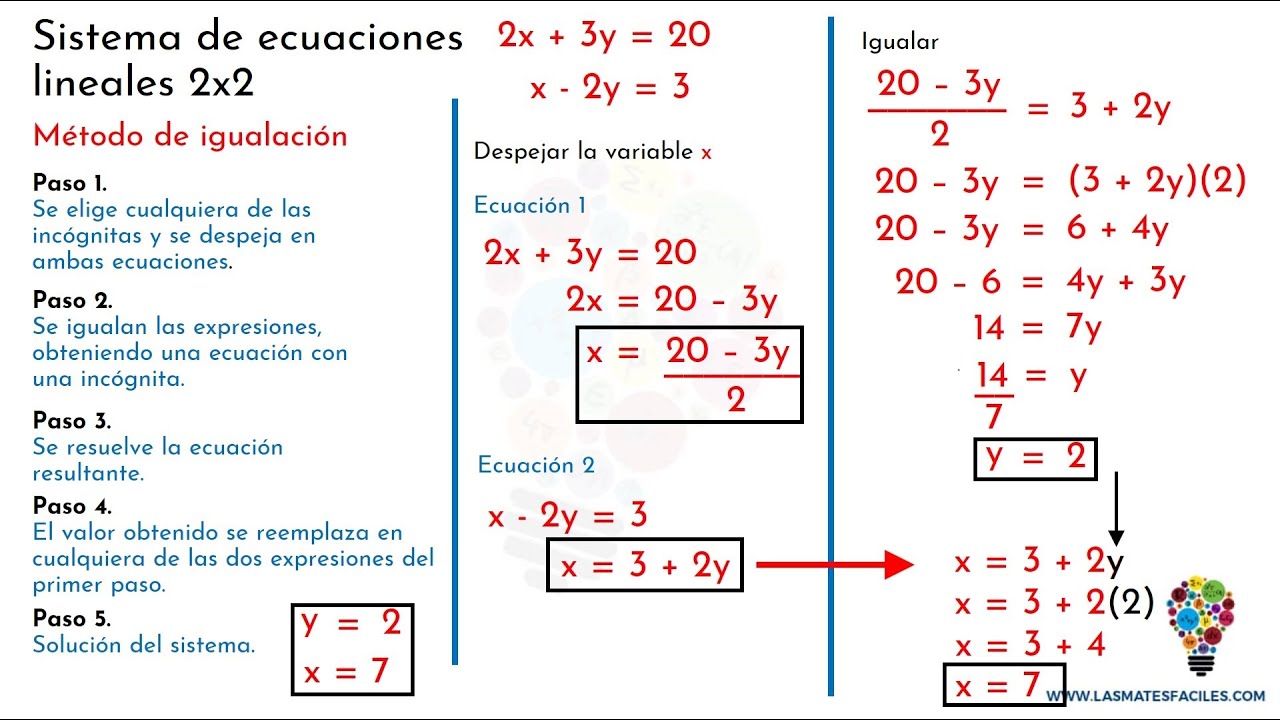
Sistemas de Ecuaciones 2x2 - Método de Igualación

09. ¿Qué es un sistema de ecuaciones lineales con dos incógnitas?

Sistemas de ecuaciones lineales 2x2 INTRODUCCIÓN

SISTEMAS DE ECUACIONES - LOS 3 MÉTODOS EXPLICADOS!

Método de CRAMER para resolver SISTEMAS 📝 Sistemas de Ecuaciones

1 Introducción Sistema de Ecuaciones
5.0 / 5 (0 votes)
