SISTEMAS DE ECUACIONES - LOS 3 MÉTODOS EXPLICADOS!

Summary

En este video, se explica de manera clara cómo resolver un sistema de ecuaciones utilizando tres métodos principales: sustitución, reducción (eliminación) e igualación. Se presentan ejemplos detallados de cada método, mostrando cómo despejar variables, eliminar términos y resolver las ecuaciones para encontrar los valores de las incógnitas. A través de estos métodos, los estudiantes pueden comprender diferentes enfoques para llegar a la misma solución, mejorando su habilidad para manejar sistemas de ecuaciones en álgebra.

Takeaways

• 😀 Se presentan los métodos de resolución de sistemas de ecuaciones: sustitución, reducción e igualación.
• 😀 El método de sustitución implica despejar una variable y sustituir su valor en otra ecuación.
• 😀 En el ejemplo dado, se trabaja con el sistema de ecuaciones 5x - 3y = 11 y 4x + y = 2.
• 😀 Se realizan operaciones algebraicas para obtener los valores de las variables en el sistema.
• 😀 El método de reducción consiste en sumar o restar ecuaciones para eliminar una variable.
• 😀 Se demuestra que la solución de los sistemas de ecuaciones puede ser verificada al sustituir los valores obtenidos.
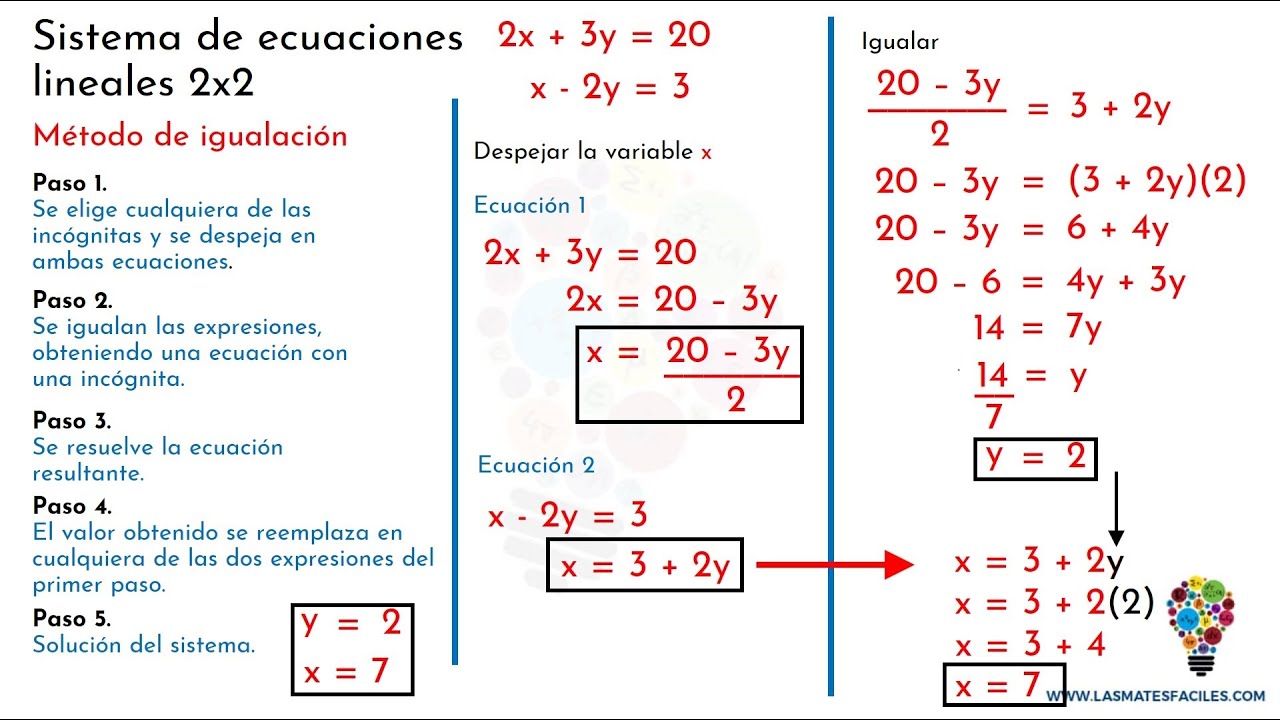
• 😀 En el método de igualación, se despejan las variables en ambas ecuaciones y se igualan las expresiones.
• 😀 Se enfatiza la importancia de tener un denominador común para facilitar la suma de fracciones en las ecuaciones.
• 😀 Se muestra cómo todos los métodos conducen a los mismos resultados en diferentes etapas del proceso.
• 😀 El conocimiento de estos métodos es esencial para resolver problemas matemáticos de manera eficiente.

Q & A

¿Qué son los sistemas de ecuaciones?

Los sistemas de ecuaciones son conjuntos de dos o más ecuaciones que comparten variables comunes y que se resuelven simultáneamente.

¿Cuáles son los métodos utilizados para resolver sistemas de ecuaciones mencionados en el video?

Los métodos mencionados son el método de sustitución, el método de reducción y el método de igualación.

¿Cómo funciona el método de sustitución?

El método de sustitución implica despejar una variable en una de las ecuaciones y luego sustituir esa expresión en la otra ecuación.

¿Qué pasos se deben seguir en el método de reducción?

En el método de reducción, se suman o restan las ecuaciones de manera que se elimine una variable, permitiendo resolver por la otra.

¿Cuál es el enfoque del método de igualación?

El método de igualación consiste en despejar la misma variable en ambas ecuaciones y luego igualar las expresiones resultantes.

¿Qué ejemplos de ecuaciones se utilizaron en el video?

Se utilizaron las ecuaciones 5x - 3y = 11 y 4x + y = 2 como ejemplos para ilustrar los métodos.

¿Por qué es importante tener un denominador común en algunos casos?

Tener un denominador común facilita la suma o resta de fracciones, lo que es esencial para resolver las ecuaciones correctamente.

¿Qué se debe hacer si una variable se despeja como negativo?

Si una variable se despeja como negativa, se puede considerar al resolver y realizar las operaciones correspondientes para obtener la solución positiva si es necesario.

¿Cuáles son los resultados de aplicar los tres métodos en el ejemplo dado?

Los tres métodos llevan a la misma solución para las variables, lo que muestra la consistencia de los métodos de resolución de sistemas de ecuaciones.

¿Cómo se relacionan estos métodos con la resolución de problemas reales?

Estos métodos se aplican en diversas áreas como la economía, la ingeniería y la ciencia, donde se necesita resolver problemas que involucran múltiples variables interrelacionadas.