Distancia entre Dos Puntos. FÁCIL
Summary
TLDREl script ofrece una explicación sencilla y didáctica sobre cómo calcular la distancia entre dos puntos, tanto en casos de alineación horizontal o vertical como en situaciones más complejas en el plano cartesiano. Se utiliza la fórmula del teorema de Pitágoras para calcular distancias diagonales, y se enfatiza la importancia de manejar correctamente los signos en las operaciones. El video también incluye ejemplos prácticos y consejos para evitar errores comunes, invitando a los espectadores a practicar con ejercicios y revisar sus respuestas en los comentarios.
Takeaways
- 📏 La distancia entre dos puntos alineados horizontalmente se calcula contando los espacios entre ellos.
- 📏 La distancia entre dos puntos alineados verticalmente se determina de manera similar, contando los espacios verticales.
- 📍 Para puntos no alineados, se utiliza el plano cartesiano para ubicar los puntos y calcular la distancia.
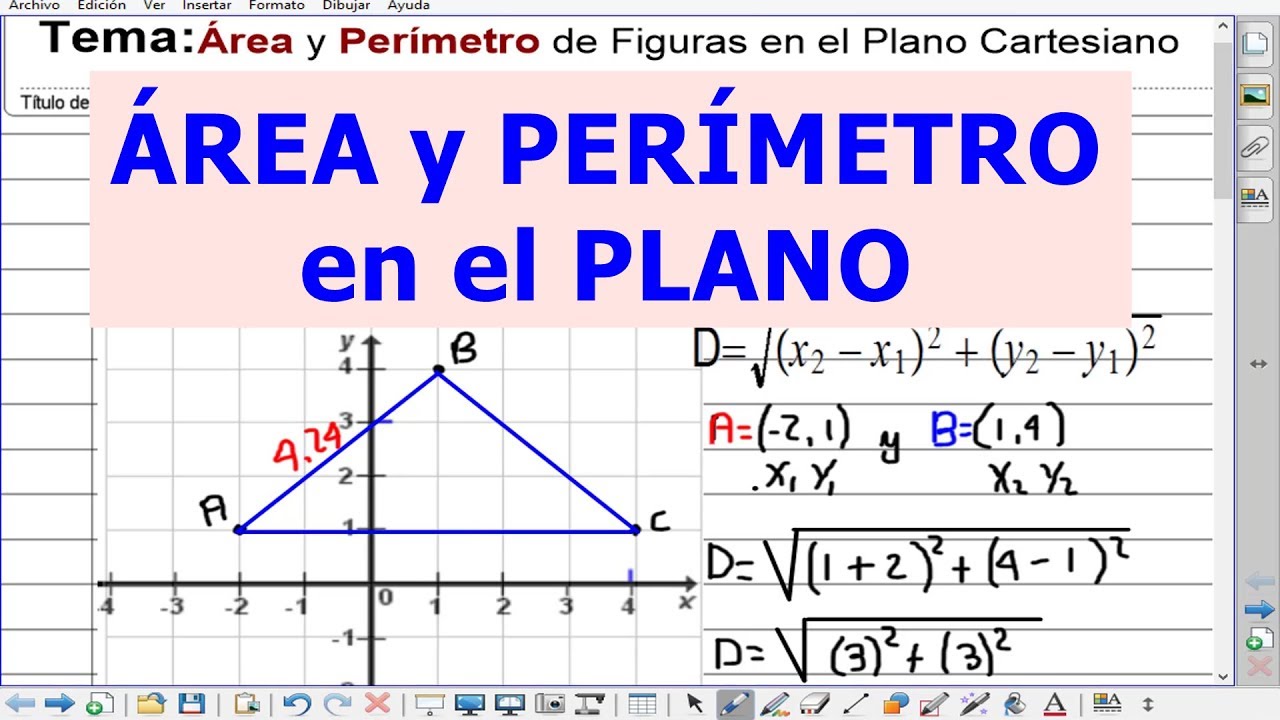
- 🔍 El Teorema de Pitágoras se aplica para calcular la distancia entre puntos en un plano cartesiano.
- ✍️ La fórmula para calcular la distancia es: \( \sqrt{(x2 - x1)^2 + (y2 - y1)^2} \), donde \( (x1, y1) \) y \( (x2, y2) \) son las coordenadas de los puntos.
- 📐 Es importante tener cuidado con los signos al realizar las operaciones dentro de la fórmula de distancia.
- 📝 Al aplicar la fórmula, se deben realizar las operaciones internas de cada paréntesis antes de sumar y calcular la raíz cuadrada.
- 📉 La ley de signos es crucial para entender cuándo se debe multiplicar o dividir con signos diferentes.
- 📚 Se ofrecen consejos para evitar errores comunes al manejar signos en cálculos, como restar y asignar el signo del número más grande.
- 📈 Se ilustra cómo realizar el cálculo de distancia directamente en un gráfico plano cartesiano, formando un triángulo rectángulo.
- 📝 Se sugiere practicar con ejercicios para mejorar la comprensión y aplicación de la fórmula de distancia entre puntos.
Q & A
¿Cómo se calcula la distancia entre dos puntos alineados horizontalmente?
-Para calcular la distancia entre dos puntos alineados horizontalmente, simplemente se cuentan los espacios que hay entre ellos. En el ejemplo dado, la distancia entre el punto A y B es de 7 unidades.
¿Y si los puntos están alineados verticalmente, cómo se calcula la distancia?
-La distancia entre dos puntos alineados verticalmente se calcula de manera similar, contando los espacios entre ellos verticalmente. En el ejemplo, la distancia entre A y B es de 5 unidades.
¿Cuál es el método para calcular la distancia entre dos puntos en un plano cartesiano que no están alineados ni horizontal ni verticalmente?
-Para calcular la distancia entre dos puntos no alineados en un plano cartesiano, se utiliza la fórmula del teorema de Pitágoras, que es √((x2 - x1)² + (y2 - y1)²).
¿Cómo se ubican las coordenadas de un punto en el plano cartesiano?
-Para ubicar las coordenadas de un punto en el plano cartesiano, se colocan los valores del eje X (horizontal, a menudo de color azul) y el eje Y (vertical, a menudo de color dorado) en sus respectivas posiciones.
¿Por qué es importante tener cuidado con los signos al aplicar la fórmula del teorema de Pitágoras?
-Es importante tener cuidado con los signos porque pueden afectar el resultado de la operación, especialmente cuando se están realizando operaciones de resta entre números con signos diferentes.
¿Cómo se resuelve el error común de aplicar la ley de signos incorrectamente al calcular distancias?
-Para evitar errores, se pueden seguir dos tips: primero, restar los números y asignar el signo del número más grande, o segundo, ver el número positivo primero y luego el negativo, asegurándose de que si es insuficiente, el resultado será negativo.
¿Cómo se calcula la distancia entre dos puntos utilizando la gráfica del plano cartesiano?
-Se forma un triángulo rectángulo uniendo los puntos por líneas vertical y horizontal. Luego, se calcula la hipotenusa, que es la distancia entre los puntos, utilizando la fórmula del teorema de Pitágoras.
¿Qué es la hipotenusa y cómo se relaciona con la distancia entre dos puntos en un triángulo rectángulo?
-La hipotenusa es el lado opuesto al ángulo recto en un triángulo rectángulo y su longitud es igual a la distancia entre los dos puntos que forman el triángulo en el plano cartesiano.
¿Por qué es más práctico realizar el cálculo de distancias directamente en la gráfica del plano cartesiano?
-Es más práctico hacerlo en la gráfica porque no se necesitan las coordenadas explícitas y se puede visualizar directamente el triángulo rectángulo formado por los puntos, lo que simplifica el proceso.
¿Qué tips se dan en el script para evitar confusiones al calcular distancias con signos negativos?
-Se dan dos tips: restar los números y asignar el signo del número más grande, y verificar primero el número positivo y luego el negativo, asegurándose de que si es insuficiente, el resultado será negativo.
¿Cuáles son algunos ejemplos de ejercicios que se pueden practicar para aplicar lo aprendido sobre el cálculo de distancias?
-El script menciona que en los comentarios se dejarán respuestas a ejercicios sobre calcular la distancia entre pares de puntos, lo cual permite a los estudiantes verificar sus soluciones y practicar el concepto.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
5.0 / 5 (0 votes)