Projectile Motion Part II | Quarter 4 Grade 9 Science Week 2 Lesson
Summary
TLDRThis video from the Maestro Techie YouTube channel dives into the intricacies of projectile motion, specifically focusing on the effects of the angle of launch on a projectile's range and height. The lesson begins with a review of the basic concepts of projectile motion, such as trajectory and the distinction between horizontal and vertical components. The video explains that while the horizontal velocity remains constant, the vertical velocity changes due to gravity's influence. It then explores the variables involved in launching a projectile at an angle and presents equations to solve problems related to projectile motion. The video highlights that the maximum range is achieved at a 45-degree angle and that a projectile launched at 30 degrees will have the same range as one launched at 60 degrees, due to these angles being complementary. An example problem is solved, calculating the maximum height and horizontal displacement of a baseball hit at a 25-degree angle with an initial velocity of 30 meters per second. The video concludes with a reminder of the impact of the angle of release on a projectile's trajectory, emphasizing the educational value of understanding these principles.
Takeaways
- 📚 Start with a review: If you missed the first week's lesson on projectile motion, check out the link in the description for an introduction to concepts like trajectory and the definition of projectile motion.
- 🚀 Understand the basics: A body in projectile motion follows a parabolic path with horizontal and vertical components, where the horizontal velocity is constant (acceleration equals zero) and the vertical acceleration is constant due to gravity (9.8 m/s²).
- 🔍 Analyze the game: Baseball is an example of projectile motion launched at an angle, illustrating how vertical velocity changes due to gravity's influence.
- 📈 Grasp the variables: In projectile launch at an angle, consider both the horizontal and vertical components of the motion.
- 📐 Initial conditions: An object projected from rest at an upward angle has an initial velocity that can be resolved into horizontal and vertical components.
- ⏱️ Time and velocity: The time it takes for an object to stop at its highest point is the same as the time it takes to return to the launch point, with the initial upward velocity being equal to the final velocity when it returns to its original height.
- 📐 Equations for solving: Learn and apply the equations for projectile motion to solve problems involving range, maximum height, and horizontal displacement.
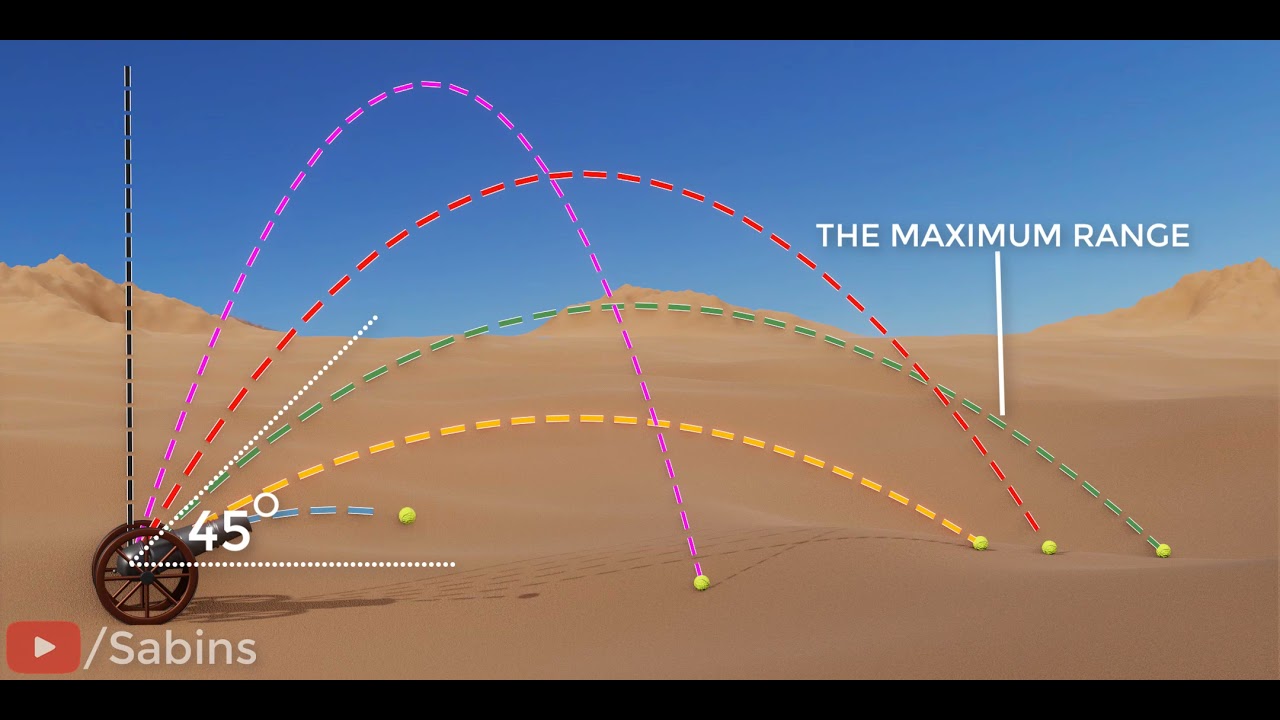
- 🎯 Optimal angle for range: The greatest range is achieved when the projectile is launched at a 45-degree angle to the horizontal.
- 📏 Complementary angles: Angles of 30 and 60 degrees are complementary and result in the same range, as do 15 and 75 degrees.
- 📈 Vertical displacement: As the angle of launch increases, the vertical displacement of the projectile also increases.
- ⏰ Time to reach max height: The time to reach the maximum height is half of the total time of flight.
- 📝 Example problem: For a baseball hit at an angle of 25 degrees with a velocity of 30 m/s, use the given formulas to calculate the maximum height and horizontal displacement of the ball.
Q & A
What is the general trajectory of a projectile in motion?
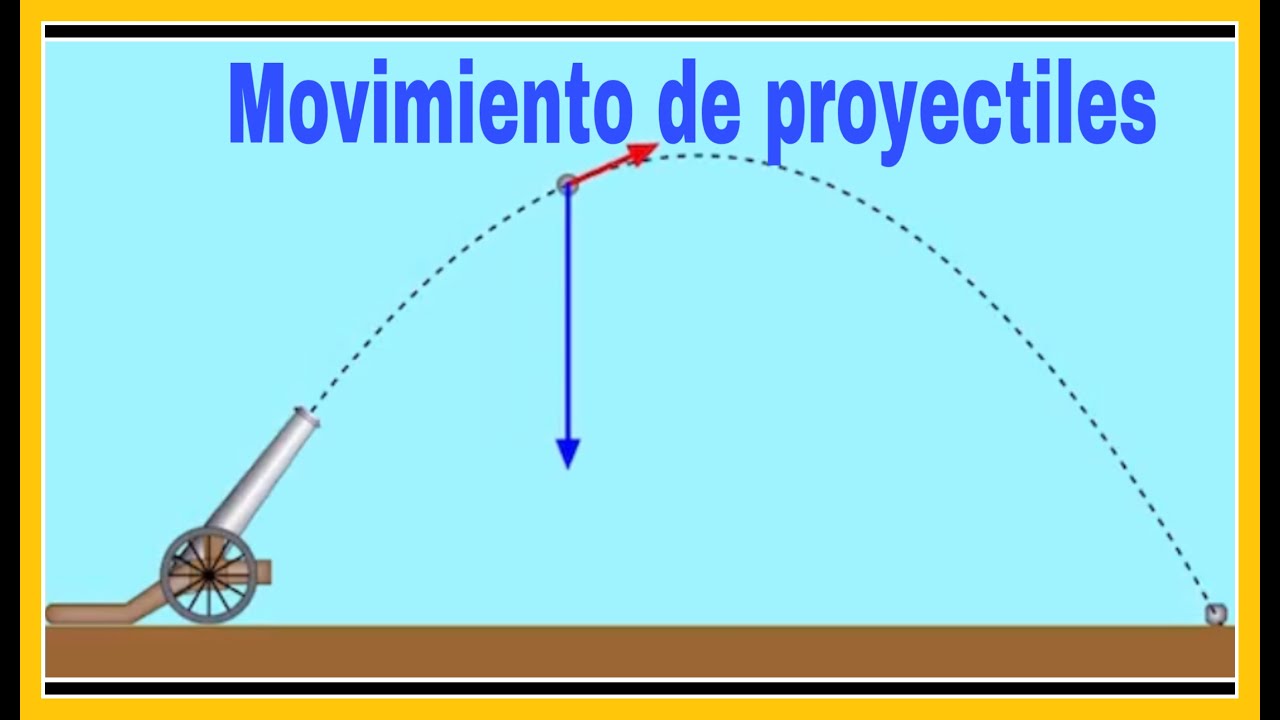
-A projectile in motion follows a parabolic trajectory, which is the result of the combination of its horizontal and vertical components of motion.
What is the acceleration of the horizontal component of projectile motion?
-The acceleration of the horizontal component of projectile motion is zero, as there are no forces acting in the horizontal direction once the projectile is launched.
What is the acceleration due to gravity and what is its value in meters per second squared?
-The acceleration due to gravity is the constant acceleration that acts on the vertical component of projectile motion, and its value is 9.8 meters per second squared.
In the context of projectile motion, what is the term for the initial speed of the object when it is launched?
-The initial speed of the object when it is launched is referred to as the initial velocity, which can be resolved into horizontal and vertical components.
What is the relationship between the angle of launch and the time it takes for a projectile to reach its highest point?
-The time it takes for a projectile to reach its highest point is the same amount of time it takes to return to the point from which it was launched, regardless of the angle of launch.
What is the maximum range achieved by a projectile launched at an angle?
-The maximum range of a projectile is achieved when it is launched at an angle of 45 degrees with respect to the horizontal.
What are complementary angles in the context of projectile motion, and how do they relate to range?
-Complementary angles in projectile motion are two angles that add up to 90 degrees, such as 30 and 60 degrees. A projectile launched at one of these angles will have the same range as if it were launched at the other angle.
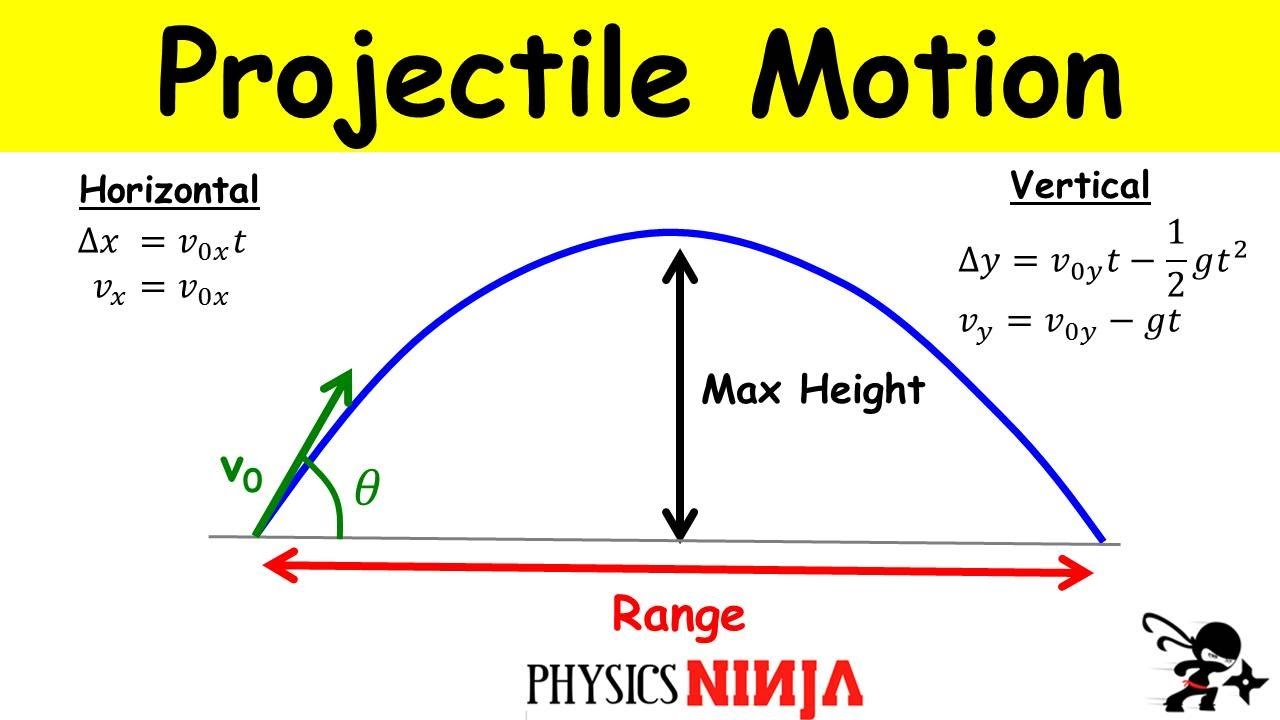
What is the formula used to calculate the maximum height reached by a projectile?
-The formula to calculate the maximum height (h) reached by a projectile is h = (v_i * sin(θ))^2 / (2 * g), where v_i is the initial velocity, θ is the angle of launch, and g is the acceleration due to gravity.
How is the horizontal displacement or range of a projectile calculated?
-The horizontal displacement or range (R) of a projectile is calculated using the formula R = v_i * cos(θ) * t, where v_i is the initial velocity, θ is the angle of launch, and t is the total time of flight.
What happens to the vertical velocity of a projectile at its highest point?
-At the highest point of its trajectory, the vertical velocity of a projectile is momentarily zero because it momentarily stops before starting to fall back down due to gravity.
What is the significance of the angle of launch in determining the range and height of a projectile?
-The angle of launch significantly affects both the range and height of a projectile. A higher angle increases the vertical displacement, while a 45-degree angle maximizes the range. Complementary angles result in the same range due to symmetry in the projectile's trajectory.
How does the direction of gravity influence the vertical velocity of a projectile?
-The direction of gravity, which is downward, opposes the upward motion of a projectile, causing the vertical velocity to decrease as the projectile rises. Conversely, as the projectile falls back to the ground, the direction of gravity aids its motion, increasing the vertical velocity.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Projectile Motion Launched at an Angle | Height and Range | Grade 9 Science Quarter 4 Week 2

S9Q4W2 | Part 2: PROJECTILE MOTION

projectile motion explained
introduction to projectile motion
FISICA (CLASE 46) - MOVIMIENTO parabólico O MOVIMIENTO de proyectiles - MOVIMIENTO EN EL PLANO
Projectile Motion: Finding the Maximum Height and the Range
5.0 / 5 (0 votes)
