Introduction to Fourier Series - Adding Sine Waves to make Sawtooth, Square, and Triangle Waves
Q & A
Qu'est-ce qu'une série de Fourier?
-Une série de Fourier est une somme infinie de fonctions trigonométriques, généralement des sinusoïdes, qui permettent de représenter des formes complexes, comme des vagues en dents de scie ou des ondes carrées. Chaque terme de la série a une amplitude différente et une fréquence qui augmente progressivement.
Que signifie l'amplitude d'une fonction sinusoïdale?
-L'amplitude d'une fonction sinusoïdale détermine la hauteur maximale (et minimale) de l'onde. Par exemple, une fonction avec une amplitude de 1 oscille entre +1 et -1.
Qu'est-ce que la période d'une fonction sinusoïdale?
-La période d'une fonction sinusoïdale est le temps nécessaire pour qu'une onde complète un cycle, c'est-à-dire qu'elle retourne à son état initial. Par exemple, si la période est de 2, cela signifie que l'onde effectue un cycle complet tous les 2 unités.
Que se passe-t-il lorsque l'on réduit l'amplitude d'une fonction sinusoïdale?
-Lorsque l'amplitude est réduite, la hauteur de l'onde diminue. Par exemple, si l'on remplace l'amplitude de 1 par 1/2, l'onde sera deux fois moins haute.
Que se passe-t-il lorsque l'on double la fréquence d'une fonction sinusoïdale?
-Doubling la fréquence d'une fonction sinusoïdale (en doublant la valeur de 'n' dans 'sin(n pi x)') réduit la période de l'onde, la faisant osciller deux fois plus vite.
Que se passe-t-il lorsque l'on additionne plusieurs fonctions sinusoïdales?
-L'addition de plusieurs fonctions sinusoïdales crée une forme plus complexe. Par exemple, en ajoutant plusieurs ondes sinusoïdales avec des amplitudes et des fréquences différentes, on peut générer des formes comme une onde en dents de scie ou une onde carrée.
Pourquoi l'ajout de termes impairs dans la série de Fourier donne-t-il une onde carrée?
-Lorsque l'on ajoute uniquement les termes impairs dans la série de Fourier (comme sin(1 pi x), sin(3 pi x), etc.), la fonction résultante approche d'une onde carrée avec des bords nets et des transitions abruptes entre les niveaux.
Pourquoi les termes de la série de Fourier qui sont les inverses des carrés des nombres impairs produisent-ils une forme de dents de scie?
-Les termes de la série de Fourier qui utilisent des inverses des carrés des nombres impairs (comme 1/1, 1/9, 1/25, etc.) génèrent une forme de dents de scie avec des coins nets. L'ajout de ces termes permet d'affiner progressivement la forme jusqu'à obtenir une approximation très nette de l'onde en dents de scie.
Quelle est la différence entre une onde en dents de scie et une onde carrée?
-Une onde en dents de scie a une montée et une descente continues et linéaires avec des coins vifs, tandis qu'une onde carrée alterne entre deux niveaux constants, créant une forme avec des transitions abruptes entre les niveaux.
Comment les séries de Fourier peuvent-elles être utilisées dans la pratique?
-Les séries de Fourier sont utilisées pour analyser et reconstruire des signaux complexes dans de nombreux domaines, y compris le traitement du signal, la compression audio, la synthèse sonore et l'analyse des phénomènes périodiques dans la physique et l'ingénierie.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
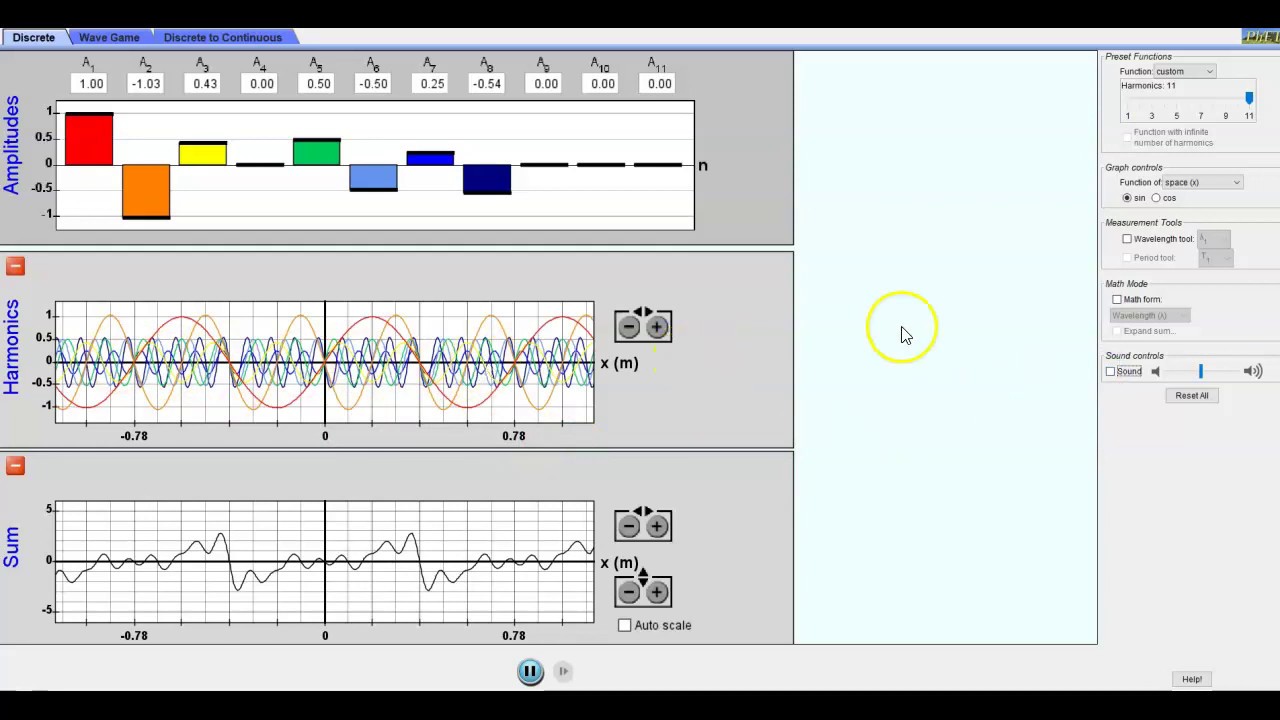
Introduction to PhET Fourier: Making Waves Simulation

The Fourier Series and Fourier Transform Demystified
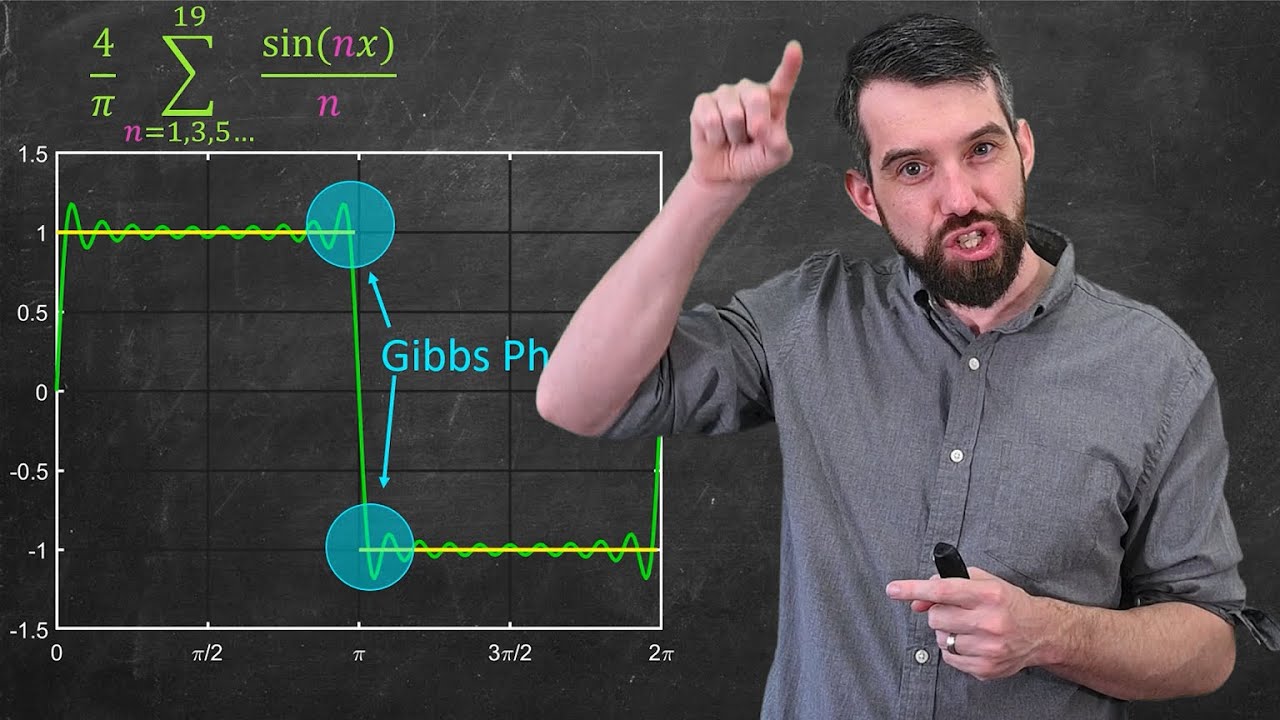
Intro to FOURIER SERIES: The Big Idea

But what is a Fourier series? From heat flow to drawing with circles | DE4
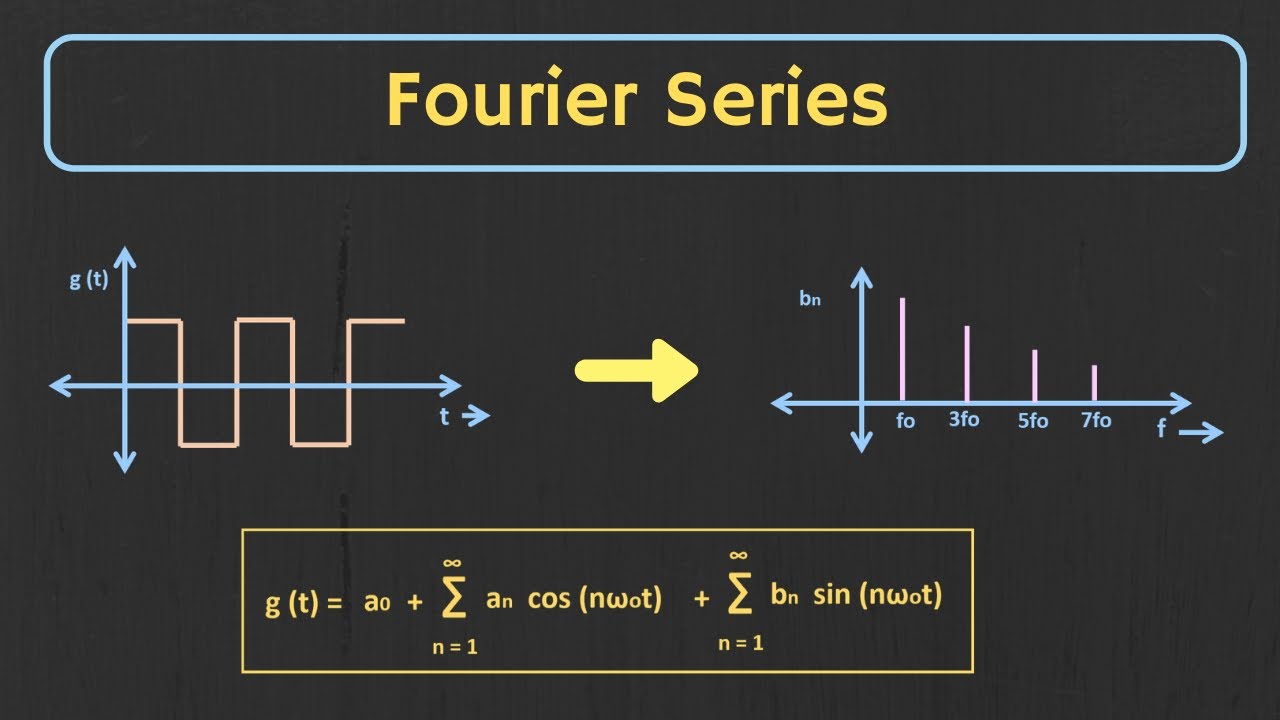
Introduction to Fourier Series | Trigonometric Fourier Series Explained
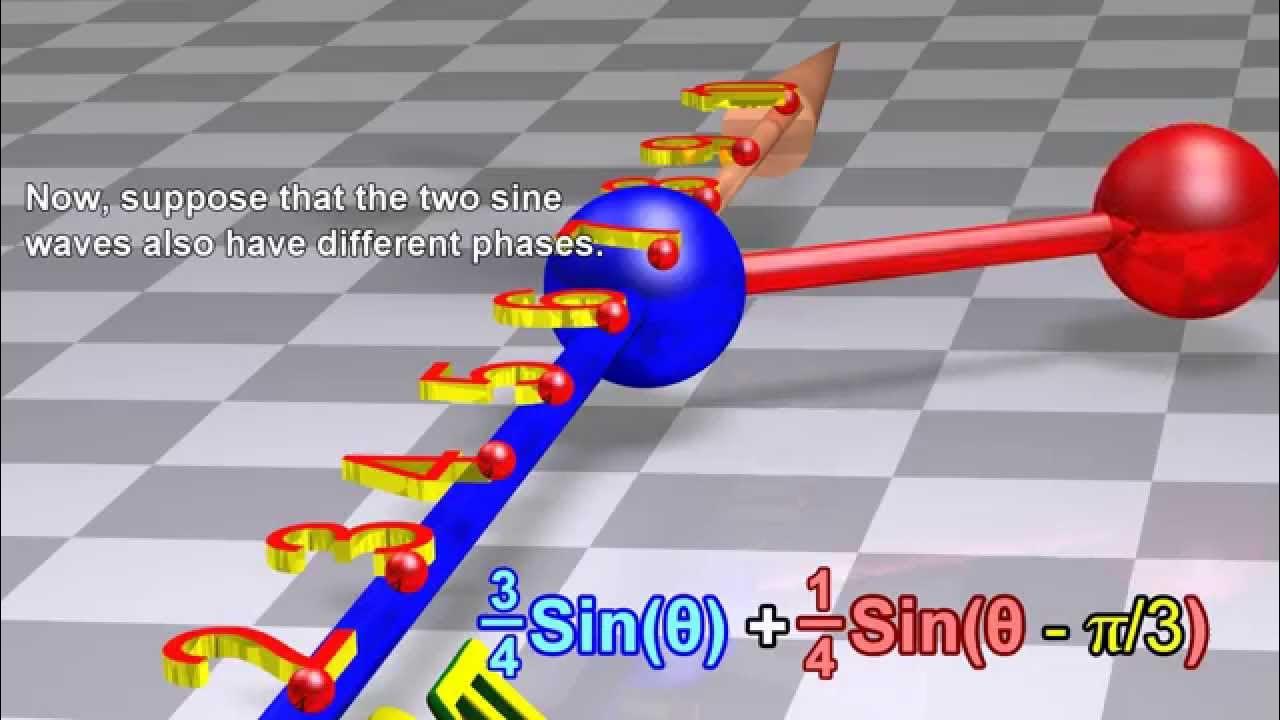
Fourier Transform, Fourier Series, and frequency spectrum
5.0 / 5 (0 votes)