Introduction to Differential Equations (Differential Equations 2)
Summary
TLDRIn this introductory video on differential equations, the speaker outlines the fundamental concepts and goals of the subject. Differential equations model real-life changes, utilizing derivatives to represent varying phenomena such as velocity and population growth. The speaker explains that solutions to these equations are functions that include arbitrary constants, which increase with the order of the equation. Additionally, they highlight the difference between ordinary and partial differential equations, emphasizing that ordinary equations typically involve a single independent variable. The video sets the stage for future lessons on verifying solutions to differential equations.
Takeaways
- 😀 Differential equations model real-life situations where change occurs, such as population growth or motion.
- 📈 The primary goal of differential equations is to represent change using mathematical functions.
- 🔄 A differential equation involves derivatives, which indicate how a quantity changes concerning another.
- 📚 Solutions to differential equations are typically functions that include arbitrary constants, reflecting an infinite family of solutions.
- 💡 The order of a differential equation is defined by the highest derivative present; for example, first-order equations have one arbitrary constant.
- 🔍 When solving a differential equation, integration introduces arbitrary constants, leading to a family of equations.
- 🧮 Initial conditions can help narrow down the infinite family of solutions to a specific solution by determining the value of arbitrary constants.
- ⚖️ There is often a balance between creating a mathematically accurate model and the ability to solve that model effectively.
- 📊 Ordinary differential equations involve one independent variable, while partial differential equations involve multiple independent variables.
- 🚀 The study of differential equations is a progression from understanding basic concepts to applying them in complex real-life scenarios.
Q & A
What is the primary goal of studying differential equations?
-The primary goal of studying differential equations is to model real-life situations and changes mathematically.
How do differential equations relate to real-life scenarios?
-Differential equations help represent changes such as velocity, acceleration, and population dynamics, capturing how these quantities change over time.
What challenges arise when creating mathematical models in differential equations?
-The challenge lies in balancing a model that accurately represents a situation with the complexity of the mathematics involved; sometimes, simplifications are made to facilitate calculations.
What is a derivative in the context of differential equations?
-A derivative represents the rate of change of a function. In differential equations, derivatives relate to how quantities change in relation to one another.
What does the term 'order' refer to in differential equations?
-The order of a differential equation refers to the highest derivative present. It determines the number of arbitrary constants in the solution.
How do arbitrary constants appear in the solutions of differential equations?
-Arbitrary constants arise when solving differential equations. For example, a first-order differential equation has one constant, while a second-order equation has two constants.
What is the significance of an initial condition in solving differential equations?
-An initial condition allows us to narrow down the general solution (family of equations) to a specific solution that passes through a given point.
What is the difference between ordinary and partial differential equations?
-Ordinary differential equations involve only one independent variable, while partial differential equations involve multiple independent variables.
What is a family of solutions in the context of differential equations?
-A family of solutions refers to the infinite set of equations derived from integrating a differential equation, each differing by arbitrary constants.
How does the process of integration relate to finding solutions for differential equations?
-Integration is used to find solutions to differential equations. When you integrate a derivative, you typically obtain a function plus an arbitrary constant, representing a family of solutions.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

A concept of Differential Equation

What is a DIFFERENTIAL EQUATION?? **Intro to my full ODE course**

Pengantar Persamaan Diferensial

🔵03 - Linear and Non-Linear Differential Equations: Solved Examples
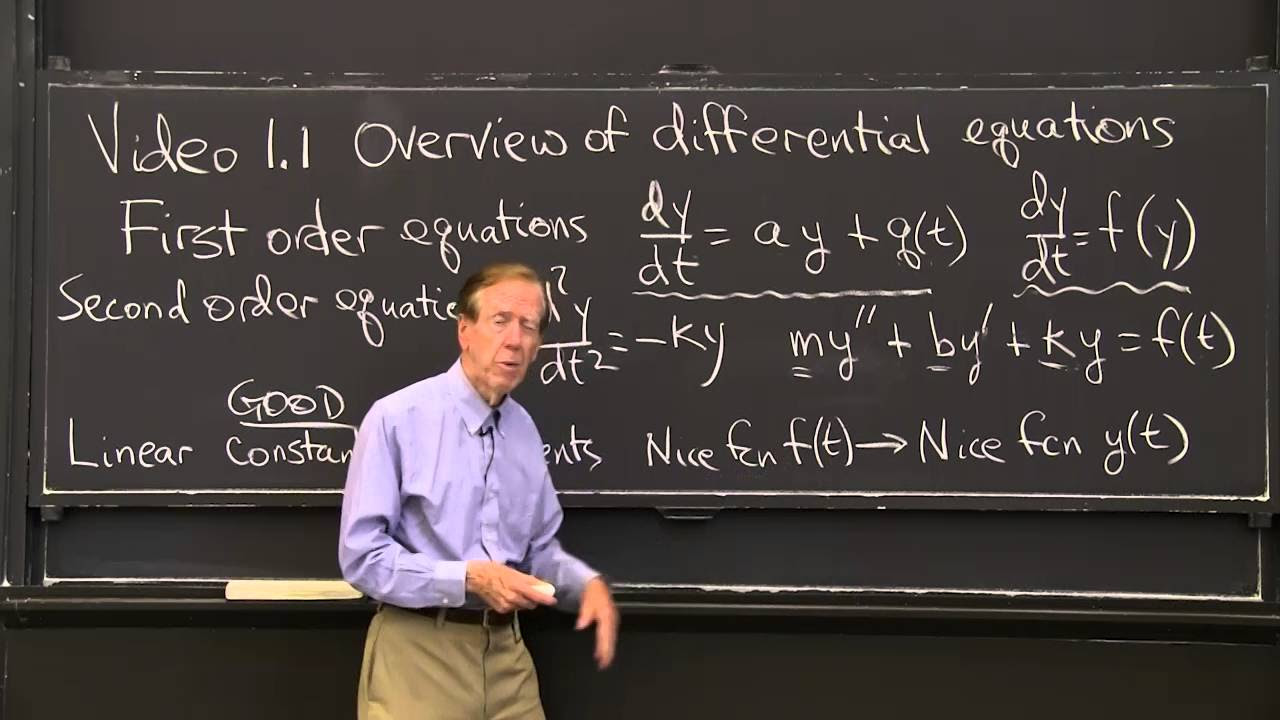
Overview of Differential Equations

Introducing Weird Differential Equations: Delay, Fractional, Integro, Stochastic!
5.0 / 5 (0 votes)
