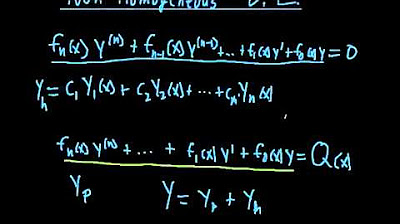🔵03 - Linear and Non-Linear Differential Equations: Solved Examples
Summary
TLDRThis video discusses the differences between linear and non-linear differential equations. Linear equations are defined as those where variables are raised only to the power of one, while non-linear equations include variables raised to higher powers or involve transcendental functions. The video outlines the conditions that define linear differential equations, including the absence of products of the dependent variable and its derivatives, and no transcendental functions. It provides examples and classifications of both linear and non-linear equations, guiding viewers through the essential concepts and techniques for understanding differential equations.
Takeaways
- 😀 Linear equations involve variables raised to the power of 1, while non-linear equations have variables raised to higher powers.
- 📊 Examples of linear equations include simple forms like Y = X, whereas non-linear examples include Y = X² + 2.
- 🔍 Non-linear equations can include transcendental functions such as cosine, exponential, and logarithmic functions.
- 📝 A linear differential equation follows the standard form: dy/dx + P(x)y = K(x), with P(x) and K(x) as functions of x.
- ⚙️ For a differential equation to be linear, it must meet three conditions regarding the dependent variable and its derivatives.
- ❗ The first condition requires the dependent variable and its derivatives to be raised only to the first power.
- 🚫 The second condition states that there should be no products of the dependent variable and its derivatives.
- 🔒 The third condition prohibits the presence of transcendental functions involving the dependent variable or its derivatives.
- ✅ If any of the three conditions are not satisfied, the differential equation is classified as non-linear.
- 🆗 Several examples are provided to classify differential equations as linear or non-linear based on the outlined criteria.
Q & A
What distinguishes linear equations from non-linear equations?
-Linear equations are characterized by variables raised only to the first power, while non-linear equations involve variables raised to powers greater than one or transcendental functions.
Can you provide an example of a linear equation?
-An example of a linear equation is Y = X, where the variable X is raised to the power of one.
What is a transcendental function?
-Transcendental functions are functions that cannot be expressed as algebraic equations, such as y = cos(x) or y = e^x.
What is the general form of a linear differential equation?
-A linear differential equation can be expressed in the form dy/dx + P(x)y = K(x), where P(x) and K(x) are functions of x.
What are the three conditions for a differential equation to be considered linear?
-1) The dependent variable and all its derivatives must only be to the first power; 2) There should not be any products of the dependent variable and its derivatives; 3) There should not be any transcendental functions of the dependent variable or its derivatives.
What happens if a differential equation violates any of the three linearity conditions?
-If a differential equation violates any of the three conditions, it is classified as a non-linear differential equation.
Can you give an example of a non-linear differential equation?
-An example of a non-linear differential equation is dy/dx + y^2 = 0, where the dependent variable y is raised to the power of two.
How does the presence of transcendental functions affect the classification of differential equations?
-If a differential equation contains transcendental functions of the dependent variable or its derivatives, it is classified as non-linear.
Why is the equation dy/dx + y = x^2 considered a linear differential equation?
-This equation satisfies all three linearity conditions: y and dy/dx are both raised to the first power, there are no products of y and its derivatives, and there are no transcendental functions.
What is the significance of classifying differential equations as linear or non-linear?
-Classifying differential equations helps determine the appropriate methods for solving them, as linear equations typically allow for more straightforward solution techniques than non-linear equations.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)