Operasi Biner
Summary
TLDRThis transcript covers binary operations, focusing on basic arithmetic operations such as addition and multiplication of integers. It explains the concepts of associativity, commutativity, and identity in operations, demonstrating how they apply to mathematical sets. The speaker introduces abstract ideas of operations as mappings between sets and explores how operations can be defined with different properties, such as being associative or commutative. Additionally, the transcript delves into identity elements and inverses, concluding with a brief introduction to groups and the importance of these properties in group theory.
Takeaways
- 🔢 The speaker introduces binary operations and gives examples like addition and multiplication of integers.
- ➕ Addition on integers is a binary operation that maps pairs of integers to another integer.
- 🔗 Operations can be defined as mappings or functions between pairs of elements from a set.
- 📊 A binary operation can be described using an operation table, allowing for flexible and arbitrary definitions.
- 🔄 The speaker explains key properties of operations like commutativity and associativity.
- ⚖️ Commutative operations satisfy the property a*b = b*a for all elements in the set.
- 🌀 Associative operations satisfy the property (a*b)*c = a*(b*c) for all elements in the set.
- ⚙️ The speaker explores how to define operations that may or may not satisfy these properties using examples.
- 🔑 Identity elements in operations are discussed, where an element e satisfies a*e = e*a = a.
- 🚫 Inverses of elements are explained, where an inverse b of an element a satisfies a*b = e, where e is the identity.
Q & A
What is the main topic of the transcript?
-The main topic of the transcript is binary operations and their properties, such as commutativity, associativity, and identity elements, in mathematical sets.
What are some common binary operations mentioned in the transcript?
-The transcript mentions common binary operations such as addition and multiplication on integer sets and the general properties these operations possess.
How is a binary operation defined in the context of sets?
-A binary operation on a set is defined as a mapping from the Cartesian product of the set with itself, A × A, to the set A. This means the operation takes two elements from the set and maps them to a single element in the same set.
What does it mean for a binary operation to be commutative?
-A binary operation is commutative if, for any two elements a and b in the set, a * b = b * a. This means that changing the order of the elements does not change the result of the operation.
What does it mean for a binary operation to be associative?
-A binary operation is associative if, for any three elements a, b, and c in the set, (a * b) * c = a * (b * c). This property indicates that the grouping of elements does not affect the result of the operation.
What is an identity element in a binary operation?
-An identity element e in a binary operation is an element such that, for any element a in the set, a * e = e * a = a. It means that applying the operation with e and any other element leaves the other element unchanged.
How can binary operations be represented for finite sets?
-Binary operations on finite sets can be represented using an operation table, where the rows and columns represent elements of the set, and the cells contain the results of the operation between those elements.
What example is given in the transcript for a commutative binary operation?
-The transcript provides an example of addition on the set of real numbers ℝ. In this operation, for any two elements a and b, a + b = b + a, demonstrating commutativity.
What example is given for a non-commutative binary operation?
-An example of a non-commutative operation is given using a custom-defined operation ‘star’ where, for certain pairs of elements a and b, a * b ≠ b * a. This is shown by providing a counterexample where the results differ depending on the order of elements.
What conditions must be met for an element to be an inverse in a binary operation?
-For an element b to be an inverse of a in a binary operation with identity element e, it must satisfy a * b = b * a = e. This means that applying the operation between a and b results in the identity element.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Python Tutorial for Beginners 3: Integers and Floats - Working with Numeric Data

GCSE Python #2: Arithmetic Operations

Operaciones con Números Enteros

Jenis dan Operasi Bilangan | Pra Aljabar | Alternatifa

Math Antics - What Is Arithmetic?
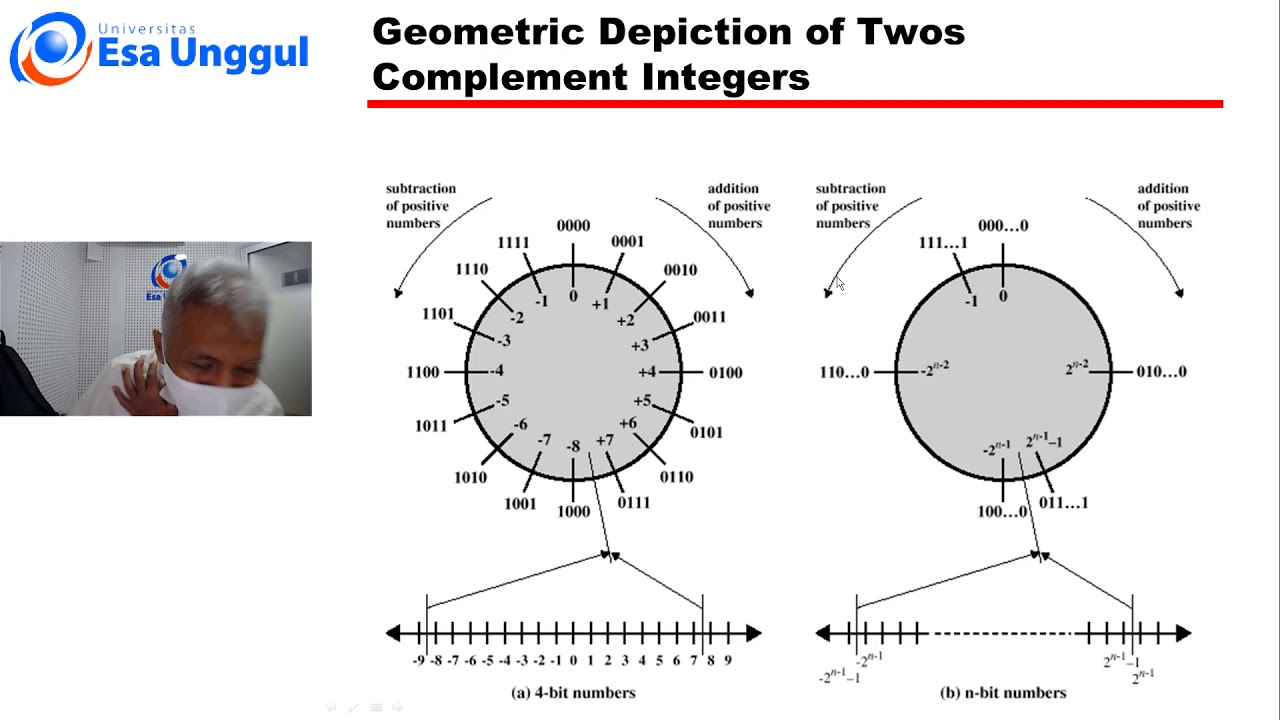
20201 - CCI120 - ORGANISASI DAN ARSITEKTUR KOMPUTER - 10 (BUDI TJAHJONO) ***
5.0 / 5 (0 votes)
