Finding Slope
Summary
TLDRThis tutorial by Miss Smith explains the concept of slope in mathematics, covering different types of slopes and how to calculate them. She demonstrates how to find slope from tables, graphs, equations, and two points, emphasizing the importance of the formula for slope (change in y over change in x). The video also introduces slope-intercept form (y = mx + b) and explains how to manipulate equations to find slope. Finally, the tutorial explores positive, negative, zero, and undefined slopes with practical examples.
Takeaways
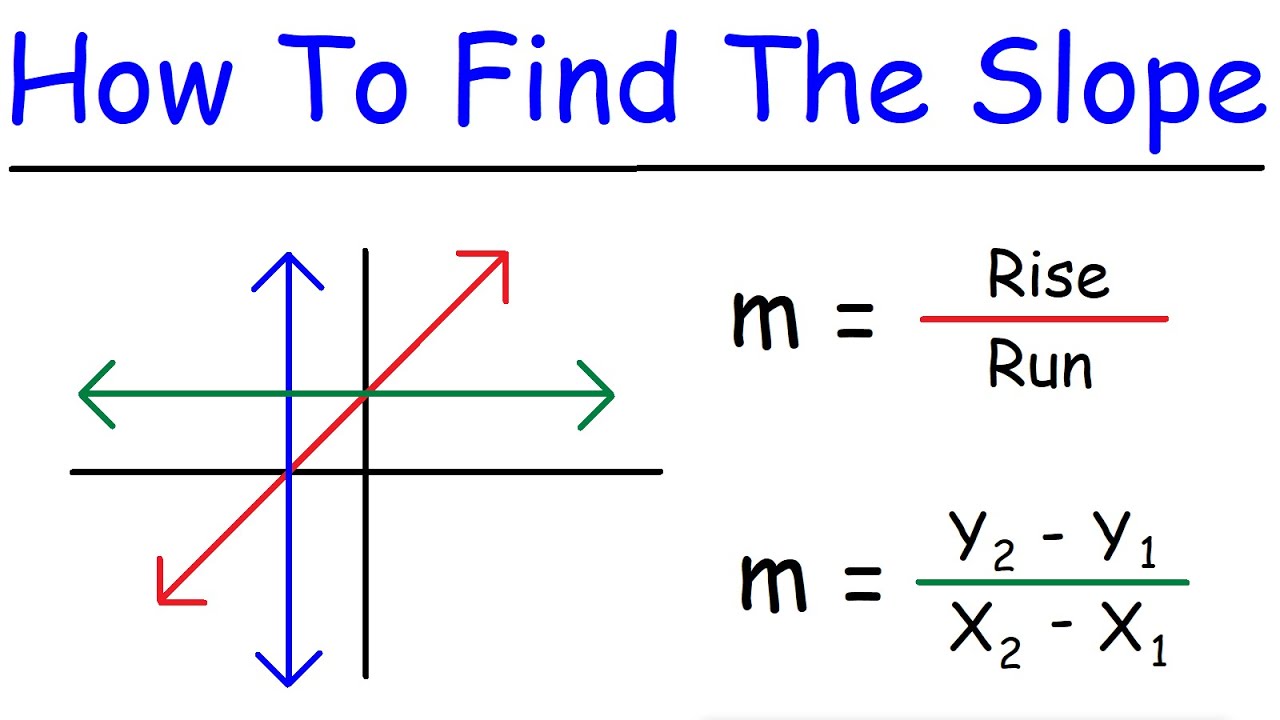
- 🎿 Slope in math is like a ski slope; it's the measure of how steep a linear line is, often expressed as 'rise over run' (change in y over change in x).
- 📊 One method to find slope is by using an XY table, identifying consistent changes in y and x values, and calculating the ratio of change in y to change in x.
- 📉 Slope can also be determined from a graph by choosing two points and calculating the rise and run between them.
- 📐 The most common form for slope calculations is the slope-intercept form: y = mx + b, where 'm' represents the slope.
- ✏️ When an equation is not in slope-intercept form, you must rearrange it by isolating y to get it into y = mx + b form to find the slope.
- 📝 Slope can be calculated from two points using the formula (y2 - y1) / (x2 - x1), which is another way of expressing the change in y over the change in x.
- 🔼 A positive slope results in an upward-sloping line, much like a roller coaster slowly climbing uphill.
- 🔽 A negative slope creates a downward-sloping line, representing a drop after the peak of a roller coaster.
- ➖ A slope of zero forms a horizontal line, where y equals a constant and no x term is present, often referred to as a 'flat horizon.'
- 🚫 An undefined slope or 'no slope' occurs with a vertical line, represented by an equation where x equals a constant.
Q & A
What is slope in mathematics, according to the video?
-In mathematics, slope represents the steepness of a linear line. It is defined as the change in y (vertical change) divided by the change in x (horizontal change), commonly referred to as 'rise over run.'
How can slope be found from a table of values?
-To find the slope from a table of values, identify the consistent changes in the y-values and the x-values. The slope is the ratio of the change in y over the change in x.
What is the importance of 'slope-intercept form' in finding slope?
-The slope-intercept form is a linear equation written as y = mx + b. In this form, the slope (m) is the coefficient of x, which directly represents the rate of change between the variables.
How do you find the slope from a graph?
-To find the slope from a graph, pick two points on the line, calculate the rise (vertical movement) and the run (horizontal movement) between the points, and then divide the rise by the run.
What formula is used to calculate slope from two points?
-The formula to calculate slope from two points is (y2 - y1) / (x2 - x1), which represents the change in y over the change in x between the two points.
What is a positive slope, and how does it appear on a graph?
-A positive slope occurs when a line is going upwards from left to right on a graph. This indicates that as x increases, y also increases.
What is a negative slope, and how does it appear on a graph?
-A negative slope occurs when a line is going downwards from left to right on a graph, meaning that as x increases, y decreases.
What does a slope of zero represent, and how is it depicted?
-A slope of zero represents a horizontal line. This indicates no vertical change as x changes, meaning the line is flat.
What is an undefined slope, and what type of line does it represent?
-An undefined slope, also known as no slope, occurs with a vertical line. In this case, the line has no run (change in x), making the slope undefined.
What are the four types of slopes mentioned in the video?
-The four types of slopes are positive slope (line going upwards), negative slope (line going downwards), zero slope (horizontal line), and undefined slope (vertical line).
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
5.0 / 5 (0 votes)