Distancia entre dos puntos

Summary

El video explica cómo calcular la distancia entre dos puntos utilizando una fórmula matemática. A través de varios ejemplos prácticos, se enseña cómo sustituir valores en la fórmula, manejando tanto números positivos como negativos. También se muestran las reglas de los signos y se resuelven ejercicios para visualizar el proceso. El objetivo es que los espectadores comprendan cómo aplicar correctamente la fórmula, incluso cuando se presentan fracciones o números con signos diferentes, logrando así calcular distancias de manera precisa.

Takeaways

• 📏 La fórmula discutida se usa para calcular la distancia entre dos puntos en un plano.
• 🔢 La fórmula incluye términos con x y y, pero el orden no afecta el resultado final ya que están sumando.
• 📍 Es importante etiquetar los puntos como punto 1 y punto 2, aunque el orden no importa.
• 📝 Para sustituir los valores en la fórmula, se deben colocar cuidadosamente las coordenadas de x1, x2, y1 y y2.
• ➕ Las restas entre números negativos pueden convertirse en sumas, aplicando la ley de signos.
• 💡 La distancia entre dos puntos se obtiene calculando la diferencia entre las coordenadas, elevándola al cuadrado, sumando ambos resultados y extrayendo la raíz cuadrada.
• 🔢 Al hacer la sustitución de valores, se deben manejar con cuidado los signos de los números para evitar errores.
• 📐 Los ejemplos mostrados en el video ilustran cómo calcular distancias entre puntos en diferentes cuadrantes del plano cartesiano.
• ✏️ Si se trabaja con fracciones, es útil convertirlas a decimales antes de proceder con los cálculos.
• 🔄 La fórmula es flexible y puede aplicarse a cualquier punto o coordenada, respetando siempre los signos y realizando las operaciones correctamente.

Q & A

¿Cuál es la fórmula utilizada para calcular la distancia entre dos puntos?

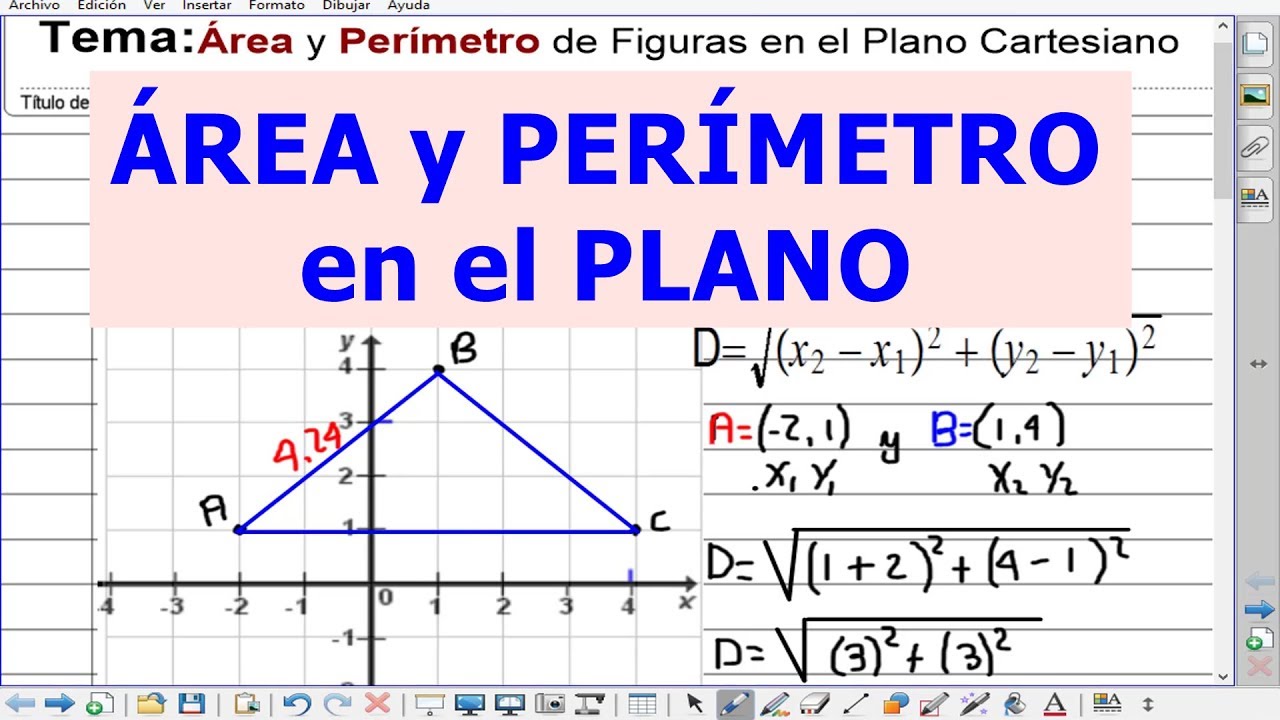
La fórmula utilizada es d = √[(x2 - x1)² + (y2 - y1)²], que permite calcular la distancia entre dos puntos en un plano.

¿Qué significa cada término en la fórmula de distancia entre dos puntos?

En la fórmula, x1 y x2 son las coordenadas en el eje x de los dos puntos, y1 y y2 son las coordenadas en el eje y de los dos puntos. La resta (x2 - x1) y (y2 - y1) encuentra las diferencias en cada eje, y luego se eleva al cuadrado para eliminar los signos negativos.

¿Es importante el orden de los puntos al aplicar la fórmula de distancia?

No, no importa el orden de los puntos al aplicar la fórmula, ya que la distancia es siempre positiva y la suma de los cuadrados eliminará cualquier diferencia de signo.

¿Qué ocurre si una de las coordenadas es negativa al sustituirla en la fórmula?

Si una coordenada es negativa, se debe respetar el signo y aplicar correctamente la ley de signos. Por ejemplo, si hay dos signos negativos juntos, se convierte en un signo positivo.

¿Cómo se sustituyen los valores de las coordenadas en la fórmula?

Se sustituyen colocando los valores de las coordenadas en la fórmula, siguiendo el orden correspondiente. Se debe tener cuidado con los signos y aplicar correctamente las operaciones de suma y resta.

¿Qué es lo que debe tenerse en cuenta al utilizar fracciones en las coordenadas?

Cuando se presentan fracciones en las coordenadas, se pueden convertir a decimales para facilitar el cálculo y sustituirlos en la fórmula de la misma manera que con los números enteros.

¿Cómo se maneja una resta entre dos valores negativos en la fórmula?

Cuando se resta un número negativo, los dos signos negativos se convierten en un signo positivo, siguiendo la ley de signos, y luego se realiza la operación correspondiente.

¿Cuál es el resultado de elevar un número negativo al cuadrado en la fórmula?

Cuando un número negativo se eleva al cuadrado, el resultado siempre es positivo, ya que el signo negativo se cancela al multiplicarse por sí mismo.

¿Qué pasos se siguen después de sustituir los valores en la fórmula?

Después de sustituir los valores en la fórmula, se realizan las operaciones dentro de los paréntesis, luego se elevan al cuadrado, se suman los resultados y finalmente se calcula la raíz cuadrada para obtener la distancia.

¿Cómo se interpreta gráficamente la fórmula de distancia?

Gráficamente, la fórmula de distancia calcula la longitud de la línea recta que conecta dos puntos en un plano cartesiano, sin importar la orientación de los puntos en el espacio.