Distancia entre dos puntos Ejemplo 1
Summary
TLDREn este video, se explica de manera clara y detallada cómo calcular la distancia entre dos puntos en el plano cartesiano utilizando la fórmula de distancia. A través de un ejemplo práctico con los puntos A (7, 4) y B (1, 4), se muestra cómo aplicar la fórmula, haciendo énfasis en el proceso de sustitución y operación de los valores en la ecuación. El contenido es accesible y adecuado para quienes desean comprender los conceptos básicos de la ecuación de la recta y la distancia entre puntos, invitando a los espectadores a seguir el curso completo para aprender más.
Takeaways
- 😀 La fórmula para calcular la distancia entre dos puntos en un plano cartesiano es: √((x₂ - x₁)² + (y₂ - y₁)²).
- 😀 El primer paso para usar la fórmula es identificar correctamente las coordenadas de los dos puntos A y B.
- 😀 En el ejemplo, se utilizan los puntos A(7,4) y B(1,4) para ilustrar el proceso de cálculo.
- 😀 El valor de las coordenadas (x₁, y₁) y (x₂, y₂) debe ser asignado de manera consistente, eligiendo un punto como A y otro como B.
- 😀 La fórmula se aplica sustituyendo los valores de x₁, x₂, y₁, y₂ en el formato de la ecuación.
- 😀 La diferencia entre las coordenadas en el eje X se calcula como x₂ - x₁, y en el eje Y como y₂ - y₁.
- 😀 Después de calcular las diferencias, cada una se eleva al cuadrado antes de sumarlas.
- 😀 Es importante recordar que cuando se eleva un número negativo al cuadrado, el resultado es positivo.
- 😀 En el caso del ejemplo, la raíz cuadrada de 36 + 4 da como resultado la raíz de 40, lo que da un valor de aproximadamente 6.32.
- 😀 El video invita a los estudiantes a continuar aprendiendo a través de un curso completo sobre ecuaciones lineales y les sugiere suscribirse al canal.
- 😀 Al final, el instructor anima a los espectadores a darle 'like' al video y seguir explorando más contenidos educativos.
Q & A
¿Cuál es la fórmula para calcular la distancia entre dos puntos en un plano?
-La fórmula para calcular la distancia entre dos puntos es: d = √((x2 - x1)² + (y2 - y1)²), donde (x1, y1) y (x2, y2) son las coordenadas de los dos puntos.
¿Cómo se identifican las coordenadas de un punto en el plano cartesiano?
-En el plano cartesiano, la primera coordenada corresponde al eje x (horizontal) y la segunda coordenada corresponde al eje y (vertical). Por ejemplo, en el punto (7,4), 7 es la coordenada x y 4 es la coordenada y.
¿Qué significa x1 y x2 en la fórmula de distancia?
-x1 y x2 son las coordenadas x de los dos puntos. El valor de x1 corresponde a la coordenada x del primer punto, y x2 a la coordenada x del segundo punto.
¿Qué significa y1 y y2 en la fórmula de distancia?
-y1 y y2 son las coordenadas y de los dos puntos. y1 es la coordenada y del primer punto y y2 la coordenada y del segundo punto.
En el ejemplo, ¿cómo se asignan las coordenadas de los puntos A y B?
-En el ejemplo, el punto A es (7, 4) y el punto B es (1, 2). A la coordenada x del punto A se le asigna x1 y a la coordenada y se le asigna y1. Para el punto B, x2 corresponde a 1 y y2 a 2.
¿Por qué se utiliza el cuadrado de las diferencias en la fórmula?
-El cuadrado de las diferencias asegura que el valor de la distancia sea positivo, ya que las diferencias pueden ser negativas. Además, el cuadrado elimina cualquier signo negativo y facilita el cálculo de la raíz cuadrada.
¿Cómo se resuelven los resultados negativos dentro de la fórmula?
-Los resultados negativos dentro de la fórmula no afectan el cálculo final porque se elevan al cuadrado. Por ejemplo, (-6)² es igual a 36, y (-2)² es igual a 4.
¿Cuál es la distancia entre los puntos A (7, 4) y B (1, 2)?
-La distancia entre los puntos A (7, 4) y B (1, 2) es aproximadamente 6.32 unidades.
¿Por qué se utiliza la raíz cuadrada en la fórmula?
-Se utiliza la raíz cuadrada para obtener la distancia real entre los dos puntos. La fórmula inicialmente calcula el valor cuadrado de las diferencias, y luego la raíz cuadrada devuelve la distancia física entre ellos en el plano.
¿Qué importancia tiene el orden de las coordenadas al aplicar la fórmula?
-El orden de las coordenadas no afecta el resultado final de la distancia, ya que las diferencias se elevan al cuadrado, lo que elimina cualquier efecto de cambio de orden en las coordenadas. Sin embargo, es importante ser consistente en la asignación de x1, x2 y y1, y2 para evitar errores en los cálculos.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
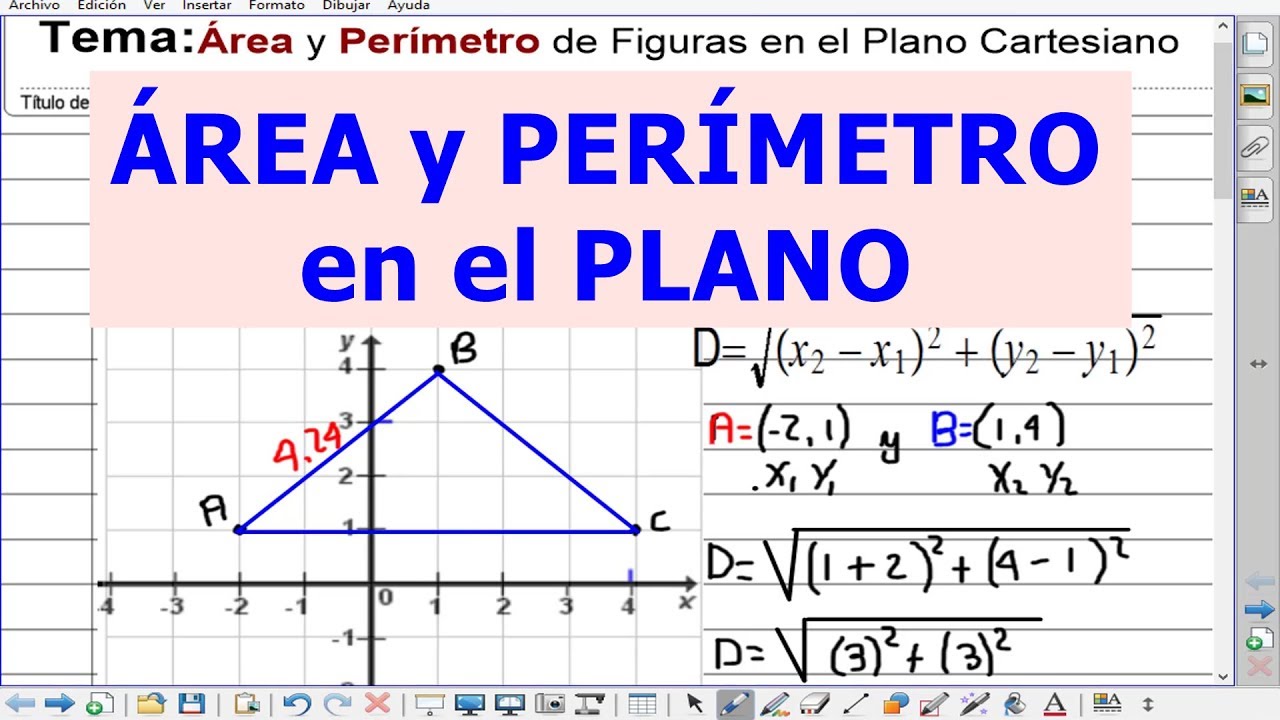
Área y Perímetro de Figuras en el Plano Cartesiano.

1. Distancia entre dos puntos. Deducción de la fórmula y ejemplos

Distancia entre dos puntos | Demostración de la fórmula

🟢 Distancia entre dos Puntos y Punto Medio✅ [EJERCICIOS RESUELTOS]
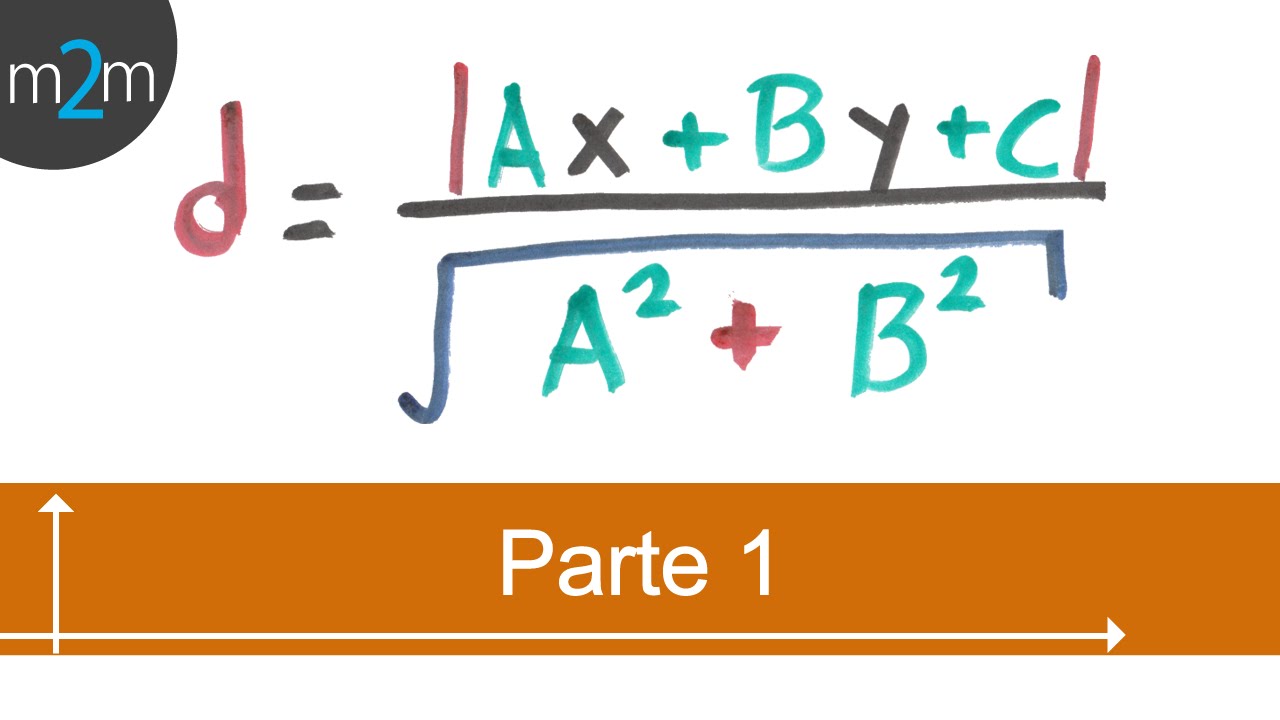
* Distancia entre un punto y una recta (PARTE 1)

Distancia Entre Dos Puntos En El Plano Cartesiano
5.0 / 5 (0 votes)
