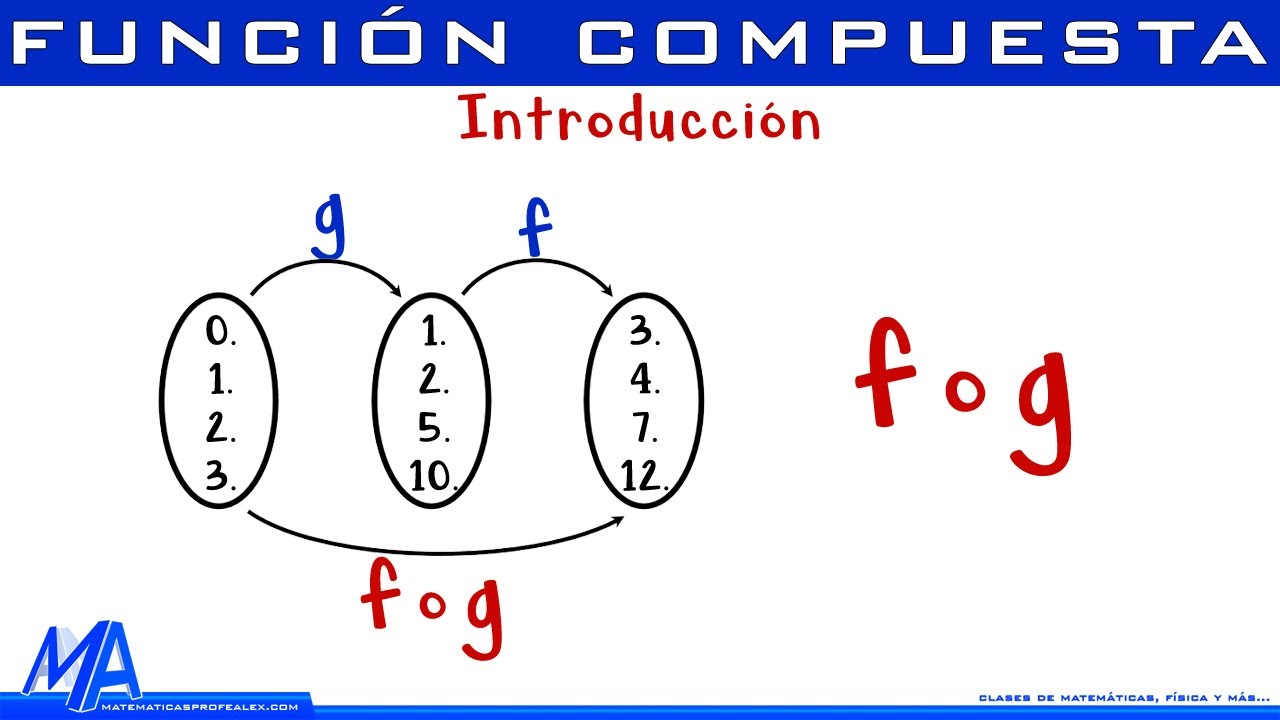
Ejercicio de razonamiento: Encontrar el valor de la función dada

Summary

En este video, se resuelve un ejercicio de composición de funciones. Dado f(x) = 12x - 1 y la composición f(g(x)) = 4x + 7, se calcula el valor de g(2) y la composición g(g(0)). El proceso incluye encontrar la expresión para g(x) y luego resolver las operaciones necesarias. Además, se presenta un desafío adicional, usando figuras para representar composiciones de funciones. El video invita a los espectadores a resolver el nuevo ejercicio propuesto y verifica las respuestas en un siguiente video. También se agradece a los seguidores por su apoyo a través de donaciones.

Takeaways

• 📘 La función f(x) = 12x - 1 y la composición de F&G de x es 4x + 7.
• 🔢 El objetivo del ejercicio es calcular g(2) + G∘G(0).
• 📐 Para resolverlo, primero se debe calcular la composición F∘G, lo que implica sustituir G(x) en f(x).
• 🔗 Se iguala la expresión de la composición F∘G con 4x + 7 para obtener una ecuación y despejar G(x).
• ➗ Se resuelve la ecuación, pasando el -1 al otro lado y dividiendo entre 2, obteniendo G(x) = 2x + 4.
• 🧮 Al evaluar G(2), se obtiene 2(2) + 4 = 8.
• 🔍 Para G∘G(0), primero se calcula G(0), obteniendo 2(0) + 4 = 4, y luego se evalúa G(4), lo que da 2(4) + 4 = 12.
• ➕ Finalmente, se suma G(2) + G∘G(0), es decir, 8 + 12, obteniendo 20.
• 📊 El video también propone un ejercicio similar con operaciones representadas mediante figuras geométricas (rectángulos y círculos).
• 🎯 Se invita a los espectadores a resolver este ejercicio, que involucra expresiones de composición con figuras.

Q & A

¿Cuál es el objetivo del video?

El objetivo del video es resolver un ejercicio matemático relacionado con la composición de funciones, utilizando como ejemplo las funciones f(x) = 12x - 1 y g(x).

¿Qué significa la composición de funciones f(g(x))?

La composición de funciones f(g(x)) significa que se reemplaza cada x en la función f por la expresión de g(x). En este caso, se sustituye g(x) en la función f(x) = 12x - 1.

¿Qué valor se obtiene al igualar la composición de f(g(x)) con 4x + 7?

Al igualar f(g(x)) = 4x + 7 y despejar g(x), se obtiene la expresión g(x) = 2x + 4.

¿Cómo se calcula g(2)?

Para calcular g(2), se sustituye x = 2 en la función g(x) = 2x + 4. El resultado es g(2) = 2(2) + 4 = 8.

¿Cómo se calcula g(g(0))?

Primero, se calcula g(0) sustituyendo x = 0 en g(x) = 2x + 4, lo que da g(0) = 4. Luego, se calcula g(g(0)) como g(4), sustituyendo x = 4, lo que da g(4) = 2(4) + 4 = 12.

¿Cuál es el resultado final de g(2) + g(g(0))?

El resultado final es g(2) + g(g(0)) = 8 + 12 = 20.

¿Qué tema plantea el video al final para que los espectadores lo resuelvan?

Al final del video, se propone un ejercicio usando operaciones representadas por figuras geométricas (rectángulo y círculo) que deben cumplir ciertas condiciones dadas.

¿Cómo se puede expresar el ejercicio propuesto al final usando funciones?

El ejercicio se puede expresar como una composición de funciones, aunque está presentado gráficamente con figuras. Las operaciones dentro de los rectángulos y círculos representan funciones matemáticas.

¿Qué significa la operación del círculo dentro de otro círculo en el ejercicio final?

La operación del círculo dentro de otro círculo en el ejercicio final representa una composición de funciones donde una función se aplica a otra función, similar a la composición f(g(x)) discutida en el video.

¿Cómo se puede apoyar al creador del video?

Se puede apoyar al creador del video mediante donaciones a través de YouTube o Patreon. También se puede dar clic en el botón de 'unirse' que aparece junto al botón de suscribirse.