Barisan dan Deret Bagian 4 - Deret Geometri Matematika Wajib Kelas 11
Summary
TLDRIn this educational video, Deni from Metlife's channel teaches viewers about geometric series, an important concept in mathematics. The video covers the formula for calculating the sum of the first n terms of a geometric series, denoted as SN. It explains how to derive the formula for SN, which involves understanding the relationship between consecutive terms and applying mathematical properties. Deni walks through five examples to demonstrate how to use the formula to solve problems related to geometric series. The video is designed to help viewers grasp the concept and apply it to various mathematical challenges.
Takeaways
- 📚 The video is an educational tutorial on geometric series, part of a larger series on sequences and series.
- 🔢 Geometric series are defined as the sum of terms in a sequence of numbers where each term is a constant multiple of the previous term.
- 📐 The nth term (UN) of a geometric series is given by the formula UN = a * r^(n-1), where 'a' is the first term and 'r' is the common ratio.
- 🧮 The sum of the first n terms of a geometric series (SN) is calculated using the formula SN = a * (1 - r^n) / (1 - r), provided r ≠ 1.
- 🔑 The formula for SN can be rearranged to SN = a * (r^n - 1) / (r - 1) when r > 1, which is useful for simplifying calculations.
- 📈 The video demonstrates how to derive the formula for SN by manipulating the series and using algebraic simplification.
- 📑 Five example problems are solved in the video, illustrating how to apply the geometric series formulas to find sums and specific terms.
- 🔍 The video explains how to identify the common ratio (r) and the first term (a) of a geometric series by examining the given terms.
- 💡 Tips are provided for simplifying calculations, such as using properties of exponents and recognizing when to apply different forms of the SN formula.
- ✅ The video concludes with a summary of the key points and an invitation to continue learning about infinite geometric series in the next tutorial.
Q & A
What is the main topic of the video?
-The main topic of the video is the explanation of geometric series, including how to derive the formula for the sum of a geometric series and how to solve problems involving geometric series.
What does SN represent in the context of the video?
-In the context of the video, SN represents the sum of the first n terms of a geometric series.
What is the formula for the nth term of a geometric series?
-The formula for the nth term (UN) of a geometric series is given by UN = a * r^(n-1), where 'a' is the first term and 'r' is the common ratio.
How is the sum of a geometric series (SN) calculated?
-The sum of a geometric series (SN) is calculated using the formula SN = a * (1 - r^n) / (1 - r), where 'a' is the first term and 'r' is the common ratio, provided that the common ratio is not equal to 1.
What is the condition for using the formula SN = a / (1 - r)?
-The formula SN = a / (1 - r) is used when the common ratio 'r' is less than 1, to avoid dealing with negative values.
What is the meaning of 'r' in a geometric series?
-In a geometric series, 'r' represents the common ratio, which is the factor by which each term is multiplied to get the next term.
How do you find the common ratio 'r' of a geometric series?
-The common ratio 'r' of a geometric series is found by dividing any term by the preceding term, i.e., r = UN / UN-1.
What is the sum of the first 10 terms of a geometric series if the first term is 16 and the common ratio is -1/2?
-Using the formula for the sum of a geometric series, S10 = 16 * (1 - (-1/2)^10) / (1 - (-1/2)), the sum of the first 10 terms is calculated to be 31/32.
How many terms are in a geometric series that sums to 363, starts with 3, and has a common ratio of 3?
-To find the number of terms in the series, use the formula SN = a * (r^n - 1) / (r - 1). Solving 363 = 3 * (3^n - 1) / (3 - 1) gives n = 5, meaning there are 5 terms in the series.
What is the sum of the first 8 terms of a geometric series if the 9th term is 128 and the 4th term is 4?
-First, find the common ratio 'r' by dividing the 9th term by the 4th term, which gives r = 32. Then, use the formula for the nth term to find 'a', which is 1/2. Finally, apply the sum formula to find S8 = 1/2 * (1 - 32^8) / (1 - 32), which results in a sum of 127.5.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Komposisi Fungsi Part 1 - Operasi Aljabar Pada Fungsi [ Matematika Wajib Kelas X ]

Kaidah Pencacahan 2 - Aturan Pengisian Tempat (Filling Slots) Matematika Wajib Kelas 12

Transformasi Geometri Bagian 5 -Transformasi Matriks Matematika Wajib Kelas 11
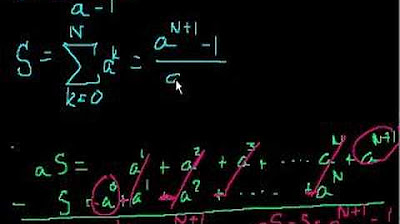
Sequences and series (part 2)

Pola Bilangan (5) | Barisan dan Deret Geometri

Asimtot Datar, Asimtot Tegak dan Asimtot Miring Fungsi Rasional Matematika Peminatan Kelas XII
5.0 / 5 (0 votes)
