Asimtot Datar, Asimtot Tegak dan Asimtot Miring Fungsi Rasional Matematika Peminatan Kelas XII
Summary
TLDRIn this educational video, Deni from Mad lem channel teaches how to determine the asymptotes of rational functions, including horizontal, vertical, and oblique asymptotes. The video covers prerequisites like polynomial factorization and limits. Deni explains that asymptotes are lines approached by curves without intersection, but they can intersect. The tutorial walks through determining vertical asymptotes by finding the zero of the denominator, horizontal asymptotes using limits as x approaches infinity, and oblique asymptotes when the degree of the numerator is higher than the denominator. Examples are provided for clarity.
Takeaways
- 📚 The video is an educational tutorial focused on teaching the determination of asymptotes of rational functions.
- 🔢 It covers three types of asymptotes: horizontal (datar), vertical (tegak), and oblique (miring).
- 📐 The presenter emphasizes prerequisite knowledge, such as polynomial factorization, polynomial division, and limits of infinity.
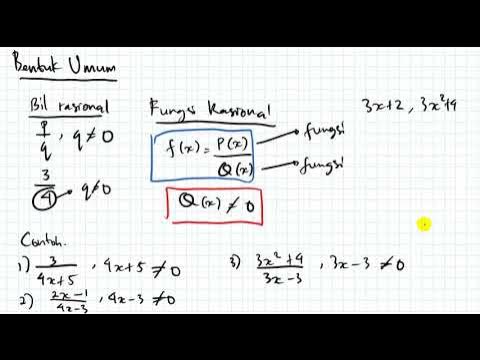
- 📉 The video explains that rational functions are ratios of two polynomials, with examples provided to illustrate the concept.
- 🌐 Asymptotes are described as lines that curves approach but never touch, with examples given for each type.
- 🚫 The video clarifies a common misconception that asymptotes never intersect their curves, showing examples where they do.
- 📌 To find vertical asymptotes, one must identify values of x that make the denominator zero, provided the numerator does not also become zero at those values.
- 📉 For horizontal asymptotes, the presenter teaches using limits as x approaches infinity to determine the asymptote's equation.
- 📈 The method for finding oblique asymptotes involves dividing the highest degree terms of the numerator by those of the denominator.
- 📝 The tutorial includes practical examples and step-by-step calculations to solve for asymptotes in given rational functions.
- 👋 The presenter concludes with a sign-off wishing viewers well, indicating the end of the tutorial.
Q & A
What are the different types of asymptotes discussed in the script?
-The script discusses three types of asymptotes: horizontal (asimtot datar), vertical (asimtot tegak), and oblique (asimtot miring).
What is a rational function according to the script?
-A rational function is defined as the ratio of two polynomial functions, similar to a rational number with a numerator and a denominator, but with variables involved.
What are the prerequisites mentioned in the script to understand asymptotes of rational functions?
-The prerequisites include understanding how to factor polynomials, divide polynomials, and comprehend limits of infinity.
Can an asymptote intersect with the curve it is associated with?
-Yes, an asymptote can intersect with the curve it is associated with. The script clarifies that an asymptote is characterized by approaching the curve without being concerned with whether it intersects or not.
How is a vertical asymptote determined for a rational function?
-A vertical asymptote is determined by finding the values of x that make the denominator zero, provided that these values do not also make the numerator zero, as that would result in an undefined expression.
What is the condition for a rational function to have a horizontal asymptote?
-A rational function has a horizontal asymptote if the degree of the polynomial in the numerator is less than or equal to the degree of the polynomial in the denominator.
How can you find the equation of a horizontal asymptote?
-The equation of a horizontal asymptote can be found by taking the ratio of the leading coefficients of the highest degree terms in the numerator and the denominator when the limit of the function as x approaches infinity is considered.
What is the condition for a rational function to have an oblique asymptote?
-A rational function has an oblique asymptote if the degree of the polynomial in the numerator is greater than the degree of the polynomial in the denominator.
How is an oblique asymptote different from a horizontal or vertical asymptote?
-An oblique asymptote is a slanted line that the function approaches but does not necessarily reach, unlike horizontal asymptotes which are horizontal lines and vertical asymptotes which are vertical lines.
What is the significance of the term 'asymptote' in mathematics?
-In mathematics, an asymptote is a line that a curve approaches but never reaches, no matter how far the curve extends.
How does the script illustrate the concept of an asymptote intersecting with a curve?
-The script uses the example of the function f(x) = x / (x^2 + 1) to illustrate that an asymptote (in this case, the x-axis) can intersect with the curve of the function.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
Fungsi Rasional kelas XI Matematika Tingkat Lanjut (Kurikulum Merdeka)

Graphing Rational Functions Step-by-Step (Complete Guide 3 Examples)

📚 Assíntotas Verticais, Horizontais e Inclinadas - Cálculo 1 (#11)

Relasi dan Fungsi Matematika Kelas 10 • Part 26: Fungsi Rasional Bentuk 3 - Kuadrat / Linear

Lesson 3 Rational Function (Part 1)

Relasi dan Fungsi Matematika Kelas 10 • Part 27: Soal Fungsi Rasional Bentuk 3 - Kuadrat / Linear
5.0 / 5 (0 votes)