Área aproximada por rectángulos (inscritos y circunscritos)
Summary
TLDREl guion del video explica el proceso de aproximación del área bajo una curva utilizando rectángulos inscritos y circunscritos. Se subdivide el intervalo de 0 a 1 en cinco partes iguales y se calcula el área de cada rectángulo a partir de su ancho (1/5) y su altura correspondiente a la función evaluada en puntos clave. Se suman las áreas de los cinco rectángulos para obtener una aproximación del área total. Además, se describe el cálculo de las sumatorias para obtener áreas aproximadas tanto inferiores como superiores, proporcionando un rango para el área real de la región.
Takeaways
- 📏 Se aproxima el área de una región determinada por una función y el eje x desde 0 hasta 1.
- 🔢 El intervalo de 0 a 1 se subdivide en cinco partes iguales para la aproximación.
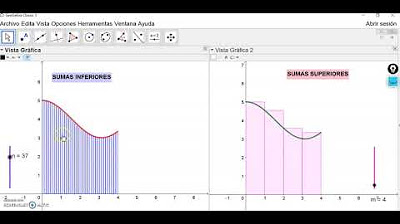
- 📐 Se utilizan rectángulos inscritos para la aproximación inferior del área.
- 📈 El área de cada rectángulo inscrito se calcula como el ancho (1/5) multiplicado por la altura correspondiente a la función evaluada en ese punto.
- 🧮 Se suman las áreas de los cinco rectángulos inscritos para obtener una aproximación del área total.
- 🔑 Se identifica un factor común (1/5) en la suma de las áreas de los rectángulos.
- 📉 Se resuelve la sumatoria de la función evaluada en puntos equidistantes para encontrar la aproximación inferior.
- 📊 Se utilizan rectángulos circunscritos para la aproximación superior del área.
- 🔼 La altura de los rectángulos circunscritos se toma del valor inicial de la función en cada subintervalo.
- 📘 Se resuelve la sumatoria de la función evaluada en los puntos iniciales de los subintervalos para encontrar la aproximación superior.
- 📋 La aproximación del área se encuentra entre las sumas de los rectángulos inscritos y circunscritos.
Q & A
¿Cuál es la función utilizada en el script para definir la región que se está aproximando?
-El script no especifica explícitamente la función, pero se describe que la región está limitada en la parte superior por una función y en la parte inferior por el eje x.
¿Cuál es el intervalo de x considerado para la aproximación del área en el script?
-El intervalo de x considerado es desde x = 0 hasta x = 1.
¿Cómo se subdivide el intervalo para la aproximación del área en el script?
-El intervalo de 0 a 1 se subdivide en cinco partes iguales para la aproximación del área.
¿Cuál es la estrategia utilizada para aproximar el área de la región en el script?
-La estrategia utilizada es sumar el área de cinco rectángulos inscritos en la región.
¿Cómo se calcula el área del primer rectángulo inscrito en el script?
-El área del primer rectángulo se calcula multiplicando su ancho, que es 1/5, por la altura, que es la función evaluada en 1/5.
¿Qué es la notación Sigma y cómo se utiliza en el script para simplificar la sumatoria?
-La notación Sigma (Σ) se utiliza para representar sumatorias, y en el script se usa para simplificar la suma de los términos correspondientes a las áreas de los rectángulos.
¿Cómo se evalúa la función para el cálculo del área de los rectángulos en el script?
-La función se evalúa sustituyendo el argumento x por los valores correspondientes a los puntos de subdivisión del intervalo, como 1/5, 2/5, 3/5, 4/5 y 5/5.
¿Qué es la fórmula que se utiliza para calcular la sumatoria de los términos I^2 en el script?
-La fórmula utilizada para calcular la sumatoria de los términos I^2 es (n(n+1)(2n+1))/6, donde n es el número de términos.
¿Cuál es la diferencia entre los rectángulos inscritos y los circunscritos mencionados en el script?
-Los rectángulos inscritos están dentro de la región y usan el valor de la función en el punto derecho para la altura, mientras que los rectángulos circunscritos están fuera de la región y usan el valor de la función en el punto izquierdo para la altura.
¿Cómo se calcula el área aproximada con rectángulos circunscritos en el script?
-El área aproximada con rectángulos circunscritos se calcula sumando el área de rectángulos donde cada uno tiene un ancho de 1/5 y una altura dada por la función evaluada en el punto izquierdo del subintervalo.
¿Cuál es el rango aproximado del área de la región según el script?
-El área de la región se encuentra entre 10/25 y 14/25 avos, según la aproximación con rectángulos inscritos y circunscritos.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
SUMAS DE RIEMANN

Área bajo la curva (Cálculo integral) Método de rectángulos. EJEMPLO 2

Área bajo la curva (Cálculo integral) Método de rectángulos. EJEMPLO 1

Método: rectángulos CIRCUNSCRITOS | Área bajo la curva | Cálculo Integral

Área bajo la curva por Extremos Derechos

Introducción al cálculo integral | Khan Academy en Español
5.0 / 5 (0 votes)
