DISTANCIA ENTRE DOS PUNTOS DEL PLANO: DEMOSTRACIÓN Y EJEMPLO
Summary
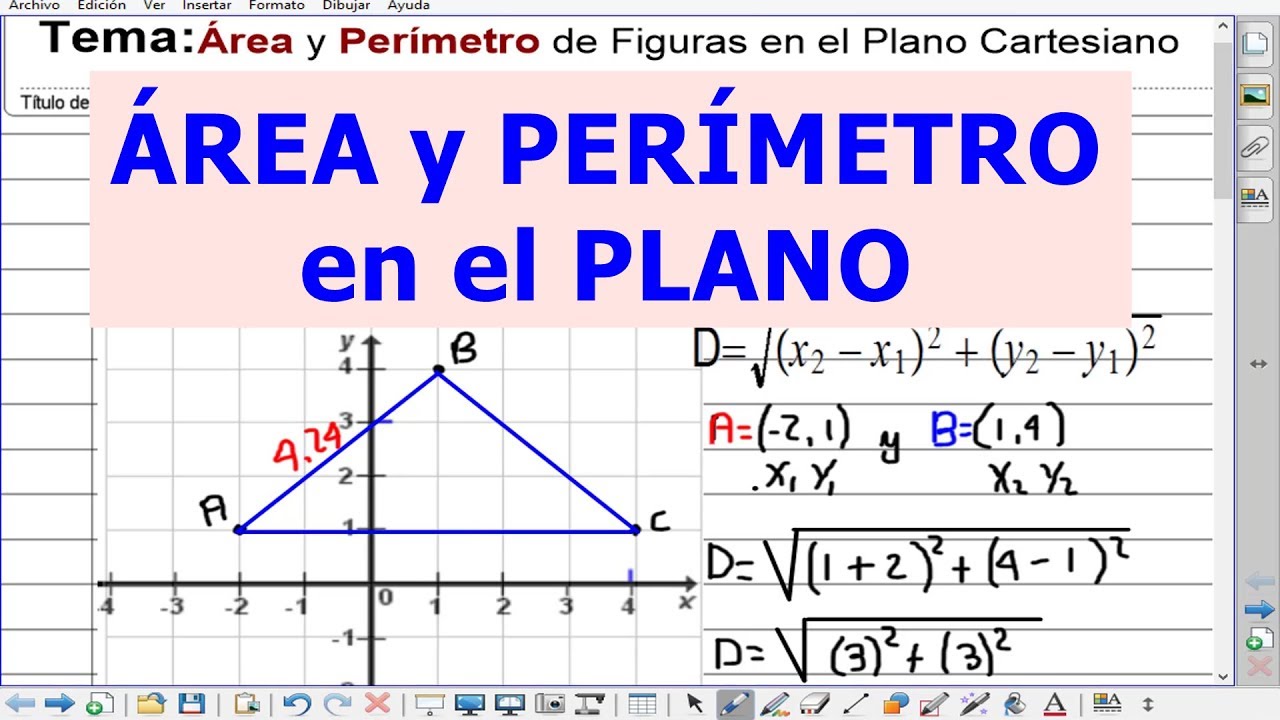
TLDREn este video, se presenta la demostración de la fórmula para calcular la distancia entre dos puntos en un plano cartesiano. Se comienza identificando dos puntos, P1 y P2, con sus respectivas coordenadas (x1, y1) y (x2, y2). Se utiliza el teorema de Pitágoras para relacionar la hipotenusa del triángulo rectángulo formado por estos puntos con sus catetos, resultando en la fórmula d = √((x2 - x1)² + (y2 - y1)²). Se aplica el ejemplo práctico de encontrar la distancia entre los puntos A(-3, 1) y B(1, -2), obteniendo un resultado de 5 unidades. Finalmente, se verifica gráficamente la distancia obtenida, confirmando la precisión del método analítico.
Takeaways
- 📚 La demostración explica cómo calcular la distancia entre dos puntos en un plano cartesiano.
- 📐 Se comienza considerando dos puntos cualesquiera, P1 y P2, con sus respectivas coordenadas (x1, y1) y (x2, y2).
- 🔍 Se utiliza un triángulo rectángulo para determinar las longitudes de los catetos, que son las diferencias entre las abscisas y ordenadas de los puntos P1 y P2.
- 📈 El teorema de Pitágoras se aplica para relacionar la longitud de la hipotenusa (la distancia entre P1 y P2) con las longitudes de los catetos.
- 🧩 Se resuelve la ecuación de Pitágoras para encontrar la longitud de la hipotenusa, que representa la distancia entre los puntos.
- 🔢 La fórmula resultante para la distancia es \( \sqrt{(x2 - x1)^2 + (y2 - y1)^2} \).
- 📝 Se proporciona un ejemplo práctico para aplicar la fórmula, donde se calcula la distancia entre los puntos A(-3, 1) y B(1, -2).
- 📊 El resultado del ejemplo muestra que la distancia entre A y B es de 5 unidades.
- 📏 Se verifica la distancia analítica con una escuadra gráfica para confirmar la precisión del cálculo.
- 🖼️ La demostración incluye una representación visual de los puntos en el plano cartesiano y el segmento entre ellos.
- 🎓 El script es una lección completa que combina teoría y práctica para entender cómo medir distancias en un plano cartesiano.
Q & A
¿Qué es la fórmula para determinar la distancia entre dos puntos en el plano cartesiano?
-La fórmula para determinar la distancia entre dos puntos en el plano cartesiano es la raíz cuadrada de la suma del cuadrado de la diferencia de las abscisas y el cuadrado de la diferencia de las ordenadas de los puntos.
¿Cómo se llaman los puntos considerados en la demostración de la fórmula?
-Los puntos considerados en la demostración son P1 y P2, donde P1 tiene coordenadas (x1, y1) y P2 tiene coordenadas (x2, y2).
¿Qué es un cateto en un triángulo rectángulo?
-Un cateto en un triángulo rectángulo es uno de los lados que forman el ángulo recto, y su longitud es la diferencia entre las coordenadas de los puntos que lo forman.
¿Cuál es el teorema aplicado para relacionar las longitudes de los lados de un triángulo rectángulo?
-El teorema aplicado es el teorema de Pitágoras, que establece que la hipotenusa al cuadrado es igual a la suma de los cuadrados de los catetos.
¿Cómo se determina la longitud de la hipotenusa en un triángulo rectángulo?
-La longitud de la hipotenusa se determina a través de la raíz cuadrada de la suma de los cuadrados de las longitudes de los catetos.
¿Por qué las distancias siempre deben ser cantidades positivas?
-Las distancias siempre deben ser positivas porque no es posible medir una distancia negativa en el espacio; la longitud de un segmento no puede ser menos que cero.
¿Cómo se aplicó la fórmula para encontrar la distancia entre los puntos A y B en el ejemplo dado?
-Se aplicó la fórmula sustituyendo las coordenadas de los puntos A y B, calculando la diferencia de las abscisas y las ordenadas, elevándolas al cuadrado y sumándolas, y finalmente tomando la raíz cuadrada del resultado.
¿Cuál es la distancia entre los puntos A y B según el ejemplo proporcionado?
-La distancia entre los puntos A y B, según las coordenadas proporcionadas en el ejemplo, es de 5 unidades.
¿Cómo se puede verificar la distancia analíticamente determinada gráficamente?
-Se puede verificar gráficamente marcando los puntos en el plano cartesiano y mediendo la longitud del segmento que los une utilizando una escuadra o herramienta similar.
¿Qué herramienta se utiliza para verificar la distancia en el plano cartesiano?
-Se utiliza una escuadra para verificar la distancia en el plano cartesiano, asegurándose de que la medida corresponda a la distancia analíticamente calculada.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

1. Distancia entre dos puntos. Deducción de la fórmula y ejemplos
Área y Perímetro de Figuras en el Plano Cartesiano.

Distancia entre dos puntos Ejemplo 1

Distancia Entre Dos Puntos En El Plano Cartesiano

Distancia entre dos puntos, usando Teorema de Pitágoras

Distancia entre dos puntos | Demostración de la fórmula
5.0 / 5 (0 votes)