Distancia entre dos puntos | Demostración de la fórmula
Summary
TLDREn este video, se explica de manera detallada cómo derivar la fórmula de la distancia entre dos puntos en el plano cartesiano. A través de un triángulo rectángulo y el teorema de Pitágoras, se demuestra que la distancia entre los puntos A(x1, y1) y B(x2, y2) es igual a la raíz cuadrada de la suma de los cuadrados de las diferencias de sus coordenadas. La fórmula resultante es: √[(x2 - x1)² + (y2 - y1)²]. El video tiene como objetivo que los estudiantes comprendan el concepto detrás de la fórmula en lugar de memorizarla, utilizando ejemplos visuales y aplicaciones prácticas.
Takeaways
- 😀 La fórmula de la distancia entre dos puntos se basa en el teorema de Pitágoras y puede ser comprendida sin necesidad de memorizarla.
- 😀 Para demostrar la fórmula, se utiliza un triángulo rectángulo formado por los puntos en el plano cartesiano.
- 😀 La distancia entre dos puntos es simplemente la longitud de la hipotenusa del triángulo rectángulo formado por las diferencias de las coordenadas en los ejes x y y.
- 😀 La fórmula de la distancia es: √((x2 - x1)² + (y2 - y1)²), donde x1, y1 son las coordenadas de un punto y x2, y2 las del otro.
- 😀 Para encontrar la distancia entre dos puntos, se calcula la diferencia entre sus coordenadas en cada eje, se eleva al cuadrado, y luego se suman las diferencias cuadradas.
- 😀 Se usa la raíz cuadrada del resultado final para obtener la distancia entre los dos puntos.
- 😀 El concepto de distancias puede ser visualizado fácilmente mediante un dibujo en el plano cartesiano.
- 😀 No es necesario saber las coordenadas exactas de los puntos para aplicar la fórmula, solo las diferencias entre ellas.
- 😀 Se pueden invertir los valores de las coordenadas al aplicar la fórmula, ya que la distancia siempre será positiva debido al cuadrado de las diferencias.
- 😀 En algunos casos, la fórmula puede escribirse de manera invertida (x1 - x2) y (y1 - y2), ya que el cuadrado de un número negativo también da positivo.
- 😀 La comprensión del concepto detrás de la fórmula, especialmente a través de un enfoque gráfico, facilita su aplicación en ejercicios y problemas.
Q & A
¿Qué se busca demostrar en este video?
-En este video se busca demostrar la fórmula de la distancia entre dos puntos en el plano cartesiano, para que los estudiantes puedan comprender de dónde proviene la fórmula en lugar de solo aprenderla de memoria.
¿Cómo se definen las coordenadas de los puntos en el plano cartesiano?
-Las coordenadas de un punto se definen mediante dos valores: la coordenada 'x' que indica su posición en el eje horizontal y la coordenada 'y' que indica su posición en el eje vertical.
¿Por qué se usan puntos ubicados en el primer cuadrante en la demostración?
-Se eligen puntos ubicados en el primer cuadrante porque es más sencillo trabajar con coordenadas positivas. Sin embargo, la demostración es válida sin importar la ubicación de los puntos.
¿Qué relación tiene la distancia entre dos puntos con un triángulo rectángulo?
-La distancia entre los dos puntos es la hipotenusa de un triángulo rectángulo cuyos catetos son las diferencias entre las coordenadas 'x' y 'y' de los puntos.
¿Cómo se calcula la distancia entre dos puntos utilizando el teorema de Pitágoras?
-La distancia entre dos puntos se calcula utilizando el teorema de Pitágoras, que establece que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. En este caso, los catetos son las diferencias entre las coordenadas 'x' y 'y'.
¿Cómo se determina la diferencia entre las coordenadas de los puntos?
-La diferencia entre las coordenadas 'x' se calcula restando la coordenada 'x' del primer punto de la coordenada 'x' del segundo punto (x2 - x1). Lo mismo se aplica para las coordenadas 'y'.
¿Por qué se puede aplicar la raíz cuadrada al resultado final en la fórmula de la distancia?
-La raíz cuadrada se aplica para eliminar el cuadrado que se encuentra en la fórmula de Pitágoras, ya que el cálculo de la distancia se realiza con las diferencias de las coordenadas elevadas al cuadrado.
¿Qué sucede si se intercambian las coordenadas en la fórmula de la distancia?
-No hay problema si se intercambian las coordenadas (por ejemplo, x1 - x2 en lugar de x2 - x1). Como la distancia es un valor positivo, el cuadrado de una diferencia siempre dará un valor positivo, independientemente del orden de la resta.
¿Cómo afecta el signo negativo en las diferencias de las coordenadas al resultado final?
-El signo negativo no afecta el resultado final porque, al elevar al cuadrado las diferencias, el valor resultante es siempre positivo. Esto asegura que la distancia entre los puntos sea siempre un valor positivo.
¿Qué importancia tiene entender la fórmula de la distancia en lugar de solo memorizarla?
-Entender la fórmula permite aplicar la lógica para resolver problemas relacionados con la distancia entre puntos en diferentes ubicaciones dentro del plano cartesiano, en lugar de depender únicamente de la memorización para resolver ejercicios.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Distancia entre dos puntos Ejemplo 1

1. Distancia entre dos puntos. Deducción de la fórmula y ejemplos
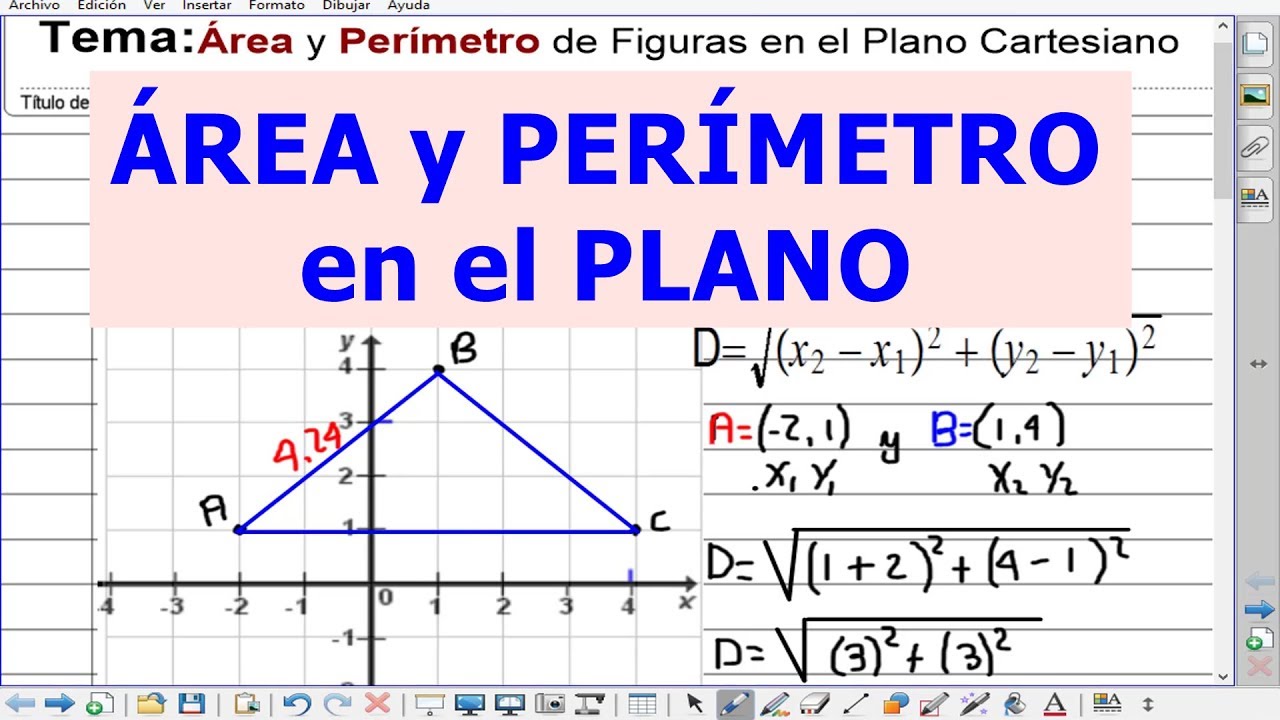
Área y Perímetro de Figuras en el Plano Cartesiano.

🟢 Distancia entre dos Puntos y Punto Medio✅ [EJERCICIOS RESUELTOS]

Punto medio entre dos puntos | Introducción

Distancia Entre Dos Puntos En El Plano Cartesiano
5.0 / 5 (0 votes)
