Week 2 Lecture 8 - Linear Regression

Summary

The script discusses the fundamentals of linear regression, emphasizing its versatility with various input types, including real-valued and qualitative data. It explains how linear regression models the expected value of y given x as a linear function, even when the input space is expanded through basis expansions or interactions. The importance of proper encoding for categorical data, such as one-hot encoding, is highlighted to avoid interference in training. The script also covers the mathematical formulation using least squares and the geometric interpretation of finding the best fit within the subspace spanned by the input vectors. It touches on challenges like dealing with non-full rank matrices and high-dimensional data, advocating for regularization techniques to ensure valid projections.

Takeaways

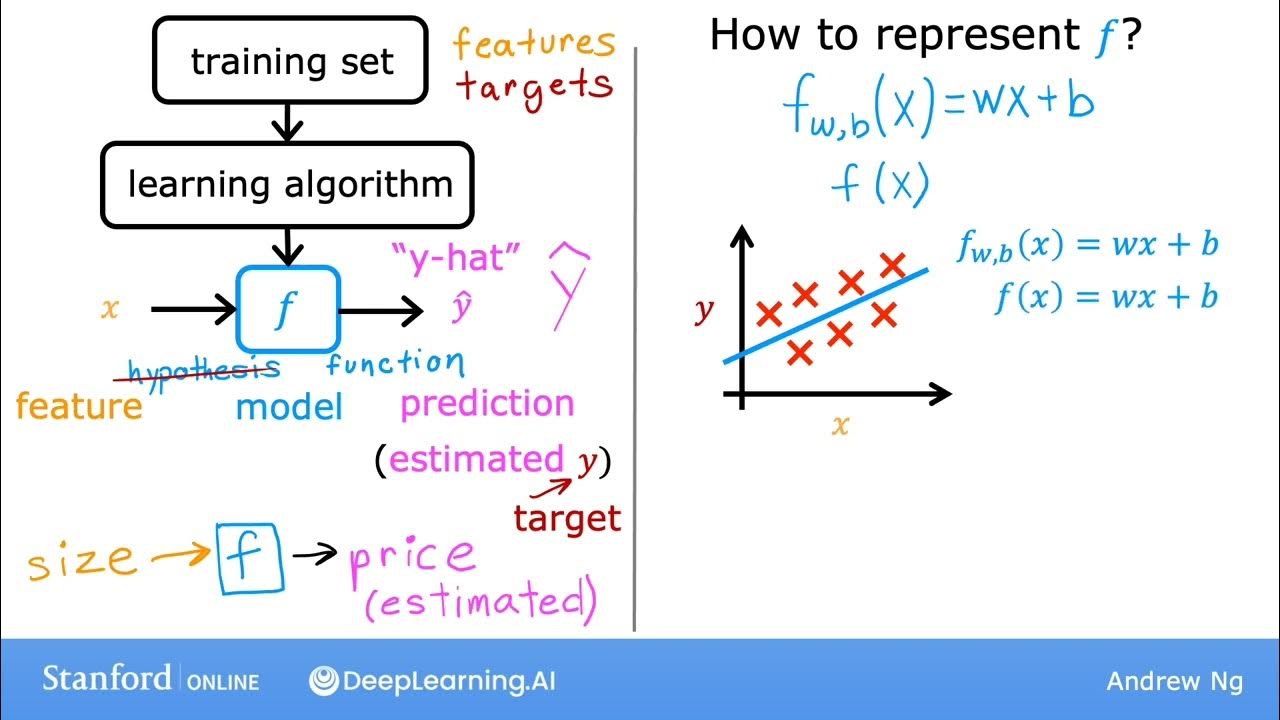
• 📉 The script assumes a linear relationship between the expected value of y given x, emphasizing the importance of linear regression in modeling.
• 🔍 x can represent a variety of inputs, not just real numbers but also encoded or transformed data, including basis expansions and interaction terms.
• 🌐 Discusses the handling of qualitative inputs, such as categorical data, through encoding methods like binary, one-of-N, or one-hot encoding.
• 🔢 The script explains that the model's complexity can be adjusted by including different orders of terms, affecting the dimensionality and the class of functions that can be modeled.
• 📚 Highlights the use of least squares for fitting the model, translating the problem into matrix notation for clarity and calculation.
• 📉 Explains the concept of the Hat matrix, which is used for estimating values and is derived from the least squares method.
• 📏 Discusses the geometric interpretation of linear regression as projecting the dependent variable Y onto the space spanned by the columns of the X matrix.
• 🚫 Points out the issues with two-bit encoding, which can lead to interference between variables, and advocates for four-bit encoding for independence.
• 📉 Clarifies that the best prediction in linear regression is the projection of Y onto the subspace spanned by the basis vectors of X.
• 🔍 Touches on the challenges of dealing with high-dimensional data where the number of dimensions (P) is greater than the number of data points (n), and the need for regularization.
• 🛠 Suggests that tools like R automatically check for full rank in the X matrix and remove redundant columns to ensure a valid projection.

Q & A

What is the basic assumption made in the context of linear regression discussed in the script?

The basic assumption is that the expected value of y given x is linear, meaning the relationship between the dependent variable y and the independent variable x can be represented by a linear function.

What does 'f(x)' represent in the script?

'f(x)' represents the expected value of y given x, which is the linear function used in linear regression to predict the output based on the input x.

What is the significance of x in the context of the script?

In the script, x can represent a variety of inputs, not just real-valued numbers. It can be drawn from a p-dimensional real-valued space, and can include different kinds of encodings or transformations of the input variables.

What is meant by 'basis expansion' in the script?

'Basis expansion' refers to a method of transforming the input space by applying some kind of transformation to the input variables, effectively increasing the dimensionality of the input space.

How can qualitative inputs be handled in linear regression?

Qualitative inputs, such as categorical data, can be handled through encoding methods like binary encoding, one-of-n encoding, or one-hot encoding, which allow these inputs to be used in the linear regression model.

What is the purpose of one-hot encoding in handling qualitative inputs?

One-hot encoding is used to represent categorical data by creating a binary column for each category, where only one column is 'hot' (i.e., has a value of 1) for any given input, ensuring that each category is represented by an independent variable in the model.

What is the geometric interpretation of linear regression as described in the script?

The geometric interpretation of linear regression is that it projects the dependent variable vector Y onto the subspace spanned by the columns of the X matrix, which represents the best possible prediction within the constraints of the linear model.

What is the 'Hat matrix' mentioned in the script?

The 'Hat matrix' is the matrix that takes the actual Y values and projects them onto the space spanned by the X matrix, effectively providing the estimated Y values (denoted as Y hat) in the linear regression model.

Why is it sometimes better to use 4 bits instead of 2 bits for encoding qualitative inputs with four categories?

Using 4 bits instead of 2 bits for encoding qualitative inputs with four categories reduces the interference between variables because each category has an independent weight in the model, which can lead to more accurate predictions with potentially less training data.

What does it mean if the X matrix in a linear regression model is not full rank?

If the X matrix is not full rank, it means that some columns are linearly dependent, and the matrix does not span a full (P+1) dimensional space. This can result in a less accurate model and may require the removal of redundant variables or the use of regularization techniques.

What is the implication of having more dimensions (P) than the number of data points (n) in a linear regression model?

Having more dimensions than data points can lead to overfitting and an unstable model. Regularization techniques are often needed to constrain the model and prevent it from fitting the noise in the data, ensuring a more generalizable prediction.