Vibraciones forzadas con dos grados de libertad
Summary
TLDREn esta clase se estudian las vibraciones forzadas con y sin amortiguamiento en sistemas con dos grados de libertad. Se realiza una analogía a sistemas con múltiples grados de libertad. Se analizan fuerzas senoidales aplicadas a masas M1 y M2 unidas por resortes, y se plantean ecuaciones matriciales para resolver el desplazamiento y las frecuencias naturales. Se discuten casos prácticos y se muestra cómo el amortiguamiento afecta la respuesta de los sistemas, destacando la importancia de encontrar el nivel óptimo de amortiguamiento para minimizar la amplitud de las vibraciones.
Takeaways
- 📚 Clase dedicada al estudio de vibraciones forzadas con y sin amortiguamiento en sistemas con dos grados de libertad.
- 🔁 Se realiza una analogía para sistemas con múltiples grados de libertad a partir de la metodología de las clases anteriores.
- 🌐 Sistema de dos masas M1 y M2 unidas por dos resortes de constantes k1 y k2, sin amortiguamiento.
- 🔧 Dos fuerzas senoidales, f1 y f2, actúan sobre las masas M1 y M2 respectivamente, a distintas frecuencias angulares omegaf.
- 📉 Se establecen las ecuaciones del movimiento para ambas masas utilizando la segunda ley de Newton.
- 🧩 Se propone un enfoque matricial para resolver el sistema, utilizando matrices de masas, rigidez y fuerzas.
- 🔢 Se calculan las frecuencias naturales de los sistemas mediante las matrices de masas y rigidez.
- 📊 Se muestra cómo las respuestas forzadas dependen de las frecuencias de forzamiento y las frecuencias naturales del sistema.
- 🏗️ Se introduce el concepto de amortiguamiento en el sistema, añadiendo fuerzas de amortiguamiento a las ecuaciones.
- 📈 Se analiza la respuesta del sistema a la frecuencia de forzamiento, destacando la importancia del factor de amortiguamiento para minimizar la amplitud de la respuesta.
- 🌐 Se extiende la discusión a sistemas con múltiples grados de libertad, manteniendo la estructura matricial para la resolución de ecuaciones.
Q & A
¿Qué sistemas se estudiarán en esta clase?
-En esta clase se estudiarán las vibraciones forzadas con y sin amortiguamiento en sistemas con dos grados de libertad y se hará una analogía en sistemas con múltiples grados de libertad.
¿Cuál es el sistema que se describe en el guión?
-El sistema descrito en el guión consiste en dos masas, M1 y M2, unidas por dos resortes de constantes k1 y k2, sin amortiguamiento, y sometidas a dos fuerzas externas, f1 y f2, ambas senoidales con frecuencias angulares omegaf.
¿Cómo se aplican las fuerzas externas en el sistema?
-La fuerza externa f1 se aplica sobre la masa 1 y la fuerza f2 se aplica sobre la masa M2, ambas con frecuencias senoidales.
¿Qué ley de Newton se utiliza para describir el movimiento de las masas?
-Se utiliza la segunda ley de Newton para describir el movimiento de las masas, relacionando la fuerza con la aceleración de las masas.
¿Cómo se puede representar el sistema de dos masas matemáticamente?
-Se puede representar el sistema de dos masas mediante una ecuación matricial que involucra la matriz de masas, la matriz de aceleraciones, la matriz de rigidez y la matriz de fuerzas.
¿Qué es la matriz de masas y cómo se relaciona con el sistema?
-La matriz de masas es una matriz que representa las masas del sistema y sus relaciones de interacción. En el caso del sistema de dos masas, se puede representar con los elementos m11, m12, m21 y m22.
¿Cómo se relacionan las frecuencias naturales con las masas y las constantes de los resortes?
-Las frecuencias naturales dependen de las masas y las constantes de los resortes. Se pueden calcular a partir de las componentes de la matriz de masas y la matriz de rigidez.
¿Qué sucede cuando la frecuencia de forzamiento es igual a la frecuencia natural?
-Cuando la frecuencia de forzamiento alcanza la frecuencia natural, la amplitud de la masa tiende a infinito, lo que indica un desplazamiento muy grande de la masa.
¿Cómo se calculan las respuestas forzadas para las masas en el sistema?
-Las respuestas forzadas para las masas se calculan a partir de la matriz de amplitudes de desplazamiento, que depende de las amplitudes de las fuerzas y las constantes k y m de las matrices de rigidez.
¿Qué cambios se introducen al considerar el amortiguamiento en el sistema?
-Al considerar el amortiguamiento, se añaden fuerzas adicionales a las ecuaciones de movimiento que corresponden a los amortiguadores con constantes c1 y c2. Esto afecta la respuesta del sistema y se debe ajustar el factor de amortiguamiento para minimizar la amplitud de la salida.
¿Cómo se relaciona el factor de amortiguamiento con la amplitud de la salida en un sistema con dos grados de libertad?
-Existe un valor óptimo de amortiguamiento que minimiza la amplitud de la salida. Si se amortigua menos que ese valor, la salida será más grande, y si se amortigua más, la vibración también será más grande.
¿Cómo se generaliza el análisis para sistemas con múltiples grados de libertad?
-El análisis se generaliza para sistemas con múltiples grados de libertad utilizando matrices de masa, amortiguamiento y rigidez de tamaño n por n, donde n es el número de grados de libertad. Las ecuaciones se resuelven de forma análoga a las de sistemas con dos grados de libertad.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
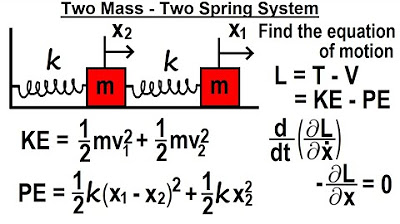
Physics 68 Lagrangian Mechanics (18 of 32) Two Mass - Two Spring System

1. Deducción de la ecuación del movimiento dinámico ẍ + 2ξωẋ + ω²x = P(t)

Engine Instrumentation Part 3 - Aircraft Gas Turbine Engines #27

Métodos y técnicas de Investigación Antropológica

⭐ Determinar el Valor de los Ángulos Suplementarios | Video 12

Uso de la tabla t-student
5.0 / 5 (0 votes)