Uso de la tabla t-student
Summary
TLDREn este video se explica cómo utilizar la tabla de distribución t-student para calcular probabilidades y cuantiles. Se describe que la distribución es simétrica y cómo se interpreta el valor de Alfa y los grados de libertad (V). Se ejemplifica cómo encontrar el cuantil que corresponde a una probabilidad de 2.5% con 7 grados de libertad, obteniendo un valor de 2.365. Además, se muestra cómo calcular la probabilidad de que una variable t con 4 grados de libertad sea mayor que 3, situando esta probabilidad entre 1% y 2.5%. El video es una guía práctica para entender y aplicar la tabla t-student en contextos de análisis estadístico.
Takeaways
- 📚 El video enseña cómo utilizar la tabla de distribución t-student para calcular probabilidades y cuantiles.
- 📉 La distribución t-student es simétrica con respecto al cero y se utiliza para encontrar valores de cuantiles específicos.
- 🔢 El valor de Alfa (α) representa la área sombreada a la derecha del cuantil, y es utilizado para buscar en la tabla.
- 📏 V, también conocido como d, representa los grados de libertad de la distribución y es crucial para la selección correcta de la fila en la tabla.
- 🔍 Los grados de libertad en el ejemplo van de 1 a 10, y los valores de Alfa mostrados son 0.05, 0.025 y 0.01.
- 🎯 Se muestra cómo encontrar el cuantil p que cumple con una probabilidad a la derecha del 2.5% con 7 grados de libertad, resultando en un valor de 2.365.
- 📊 Para calcular la probabilidad de que una variable t con 4 grados de libertad sea mayor que 3, se utiliza la tabla para encontrar el intervalo de probabilidades entre 1% y 2.5%.
- 🤔 El proceso de búsqueda en la tabla implica cruzar el valor de Alfa con el número de grados de libertad para encontrar el cuantil correspondiente.
- 📝 La tabla de distribución t-student puede tener más valores de Alfa y grados de libertad dependiendo de la edición o versión que se esté utilizando.
- 📉 El ejemplo práctico muestra cómo se usa la tabla para resolver problemas de probabilidad en estadística inferencial.
- 👋 El video concluye con un mensaje de despedida, invitando a los espectadores a seguir aprendiendo en futuras oportunidades.
Q & A
¿Qué es la tabla de distribución t-student y para qué se utiliza?
-La tabla de distribución t-student es una herramienta estadística que se utiliza para responder preguntas sobre probabilidades o para obtener cuantiles, especialmente en pruebas de hipótesis cuando se trabaja con una muestra pequeña y la desviación estándar de la población es desconocida.
¿Por qué la distribución t-student es simétrica con respecto al cero?
-La distribución t-student es simétrica con respecto al cero porque se basa en la normalidad y se utiliza para comparar la media de una muestra con la media de una población, manteniendo la simetría en torno al valor medio.
¿Qué representa el valor de Alfa (α) en la tabla de distribución t-student?
-El valor de Alfa (α) representa la área sombreada a la derecha del cuantil t sub alfa, es decir, el nivel de significancia de la prueba estadística, que indica el riesgo de rechazar un hipótesis nula verdadera.
¿Qué es V en la tabla de distribución t-student y qué representa?
-V en la tabla de distribución t-student, a veces también llamado d, representa los grados de libertad de la distribución. Es un número que se utiliza para ajustar la curva t-student según la muestra que se esté analizando.
¿Cuántos grados de libertad y valores de Alfa se muestran en la tabla del video?
-En la tabla del video se muestran grados de libertad que varían de 1 a 10 y valores de Alfa de 5%, 2.5% y 1%.
¿Cómo se encuentra el cuantil p que cumple con que a la derecha de ese cuantil hay una probabilidad del 2.5% con 7 grados de libertad?
-Se busca el valor de 0.025 en la tabla, cruzándolo con el número de grados de libertad, en este caso 7, para encontrar el valor de t que tiene una probabilidad acumulada a la derecha del 2.5%, que resultó ser 2.365.
¿Cómo se calcula la probabilidad de que la variable t con 4 grados de libertad sea mayor que tres?
-Se busca el valor de 3 en la tabla y se determina en qué intervalo de cuantiles se encuentra. En este caso, entre 2.77 y 3.74, y se interpreta que la probabilidad de que la variable t sea mayor que 3 es un valor entre 1% y 2.5%.
¿Por qué el problema de encontrar la probabilidad de que la variable t sea mayor que 3 es el 'problema contrario' al anterior?
-Se llama 'problema contrario' porque en lugar de conocer el cuantil y buscar la probabilidad asociada, en este caso se conoce la probabilidad y se busca el intervalo de cuantiles que corresponde a esa probabilidad.
¿Cuál es la probabilidad de que la variable t con distribución t y 4 grados de libertad sea mayor que 3?
-La probabilidad de que la variable t con 4 grados de libertad sea mayor que 3 es un valor que pertenece al intervalo entre 1% y 2.5%.
¿Cómo se pueden utilizar las tablas impresas de la distribución t-student en comparación con la tabla del video?
-Las tablas impresas suelen tener más valores de grados de libertad y niveles de significancia (valores de Alfa), lo que permite una mayor precisión en las consultas estadísticas y respuestas a preguntas específicas.
¿Por qué es importante conocer la tabla de distribución t-student en análisis estadísticos?
-Es importante conocer la tabla de distribución t-student porque permite realizar pruebas de hipótesis con muestras pequeñas sin conocer la desviación estándar de la población, lo que es común en muchas situaciones de investigación.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
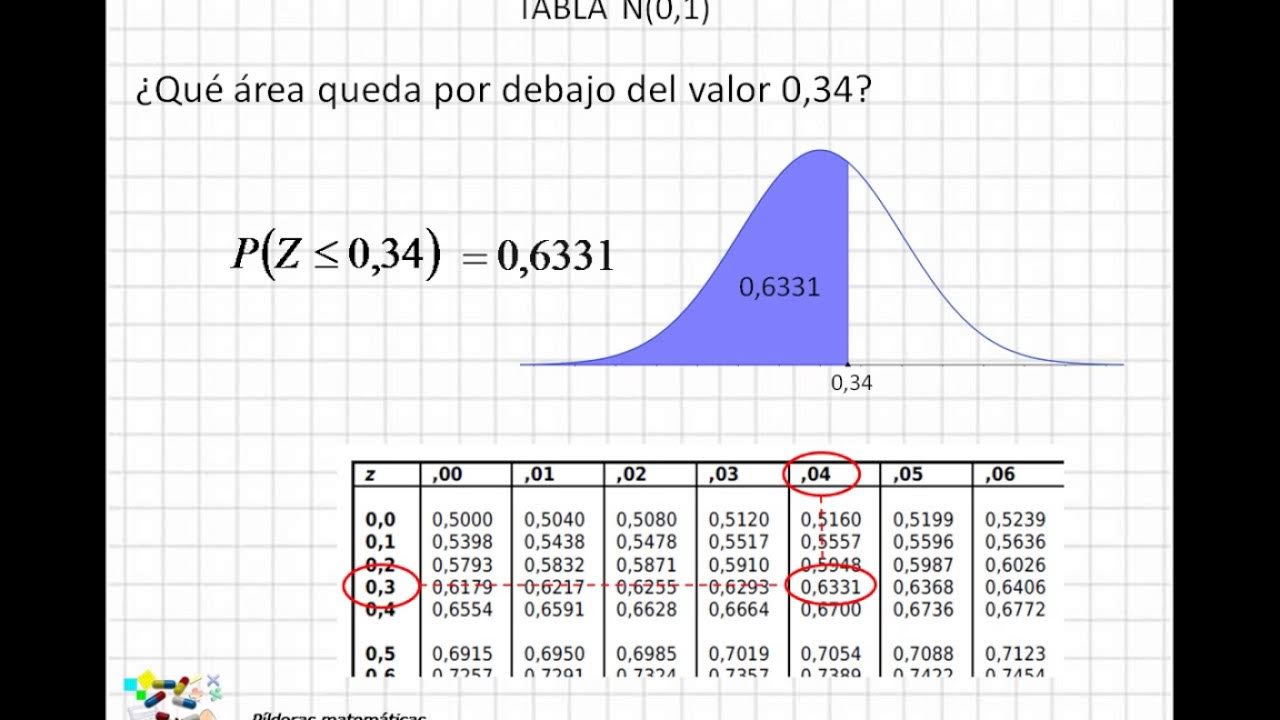
04 Cómo usar la tabla de distribución normal

DISTRIBUCIÓN F DE SNEDECOR | | UPV

Intervalos de confianza cuando se desconoce la desviación estándar poblacional
Tabla de probabilidades de la Distribucion Normal Estandar - Valores z

Distribución de probabilidad: valor esperado - ejercicio resuelto
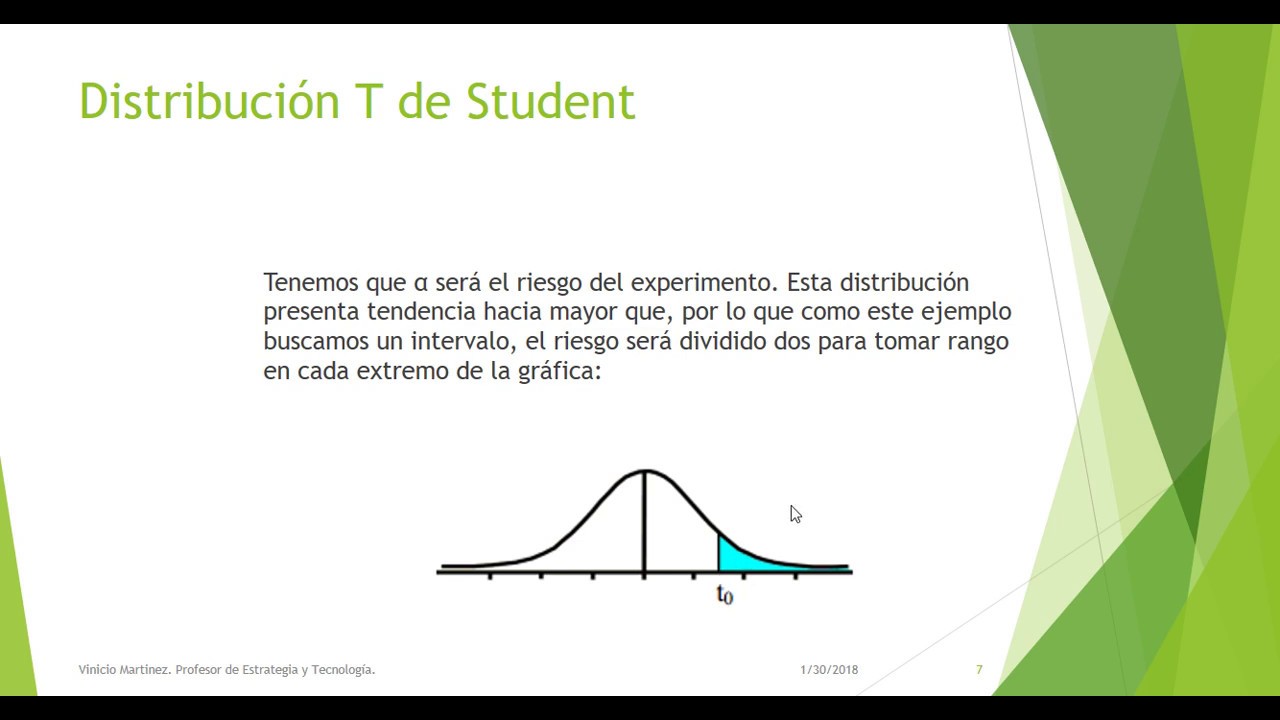
Distribución T de Student
5.0 / 5 (0 votes)
