8.01x - Lect 3 - Vectors - Dot Products - Cross Products - 3D Kinematics
Summary
TLDRIn this educational video, Professor Lewin explores the fundamentals of vectors, crucial for understanding physics. He explains scalars, vectors, their addition, and the difference between them. The lecture delves into vector decomposition, the dot and cross products, and their applications in physics. With a practical demonstration involving a moving golf ball, he illustrates the independent behavior of motion in different dimensions, emphasizing the power of vector analysis in simplifying complex physical phenomena.
Takeaways
- 📚 The lecture introduces the concept of scalars and vectors in physics, explaining that scalars like mass, temperature, and speed are described by a single number, while vectors like velocity and acceleration require both magnitude and direction.
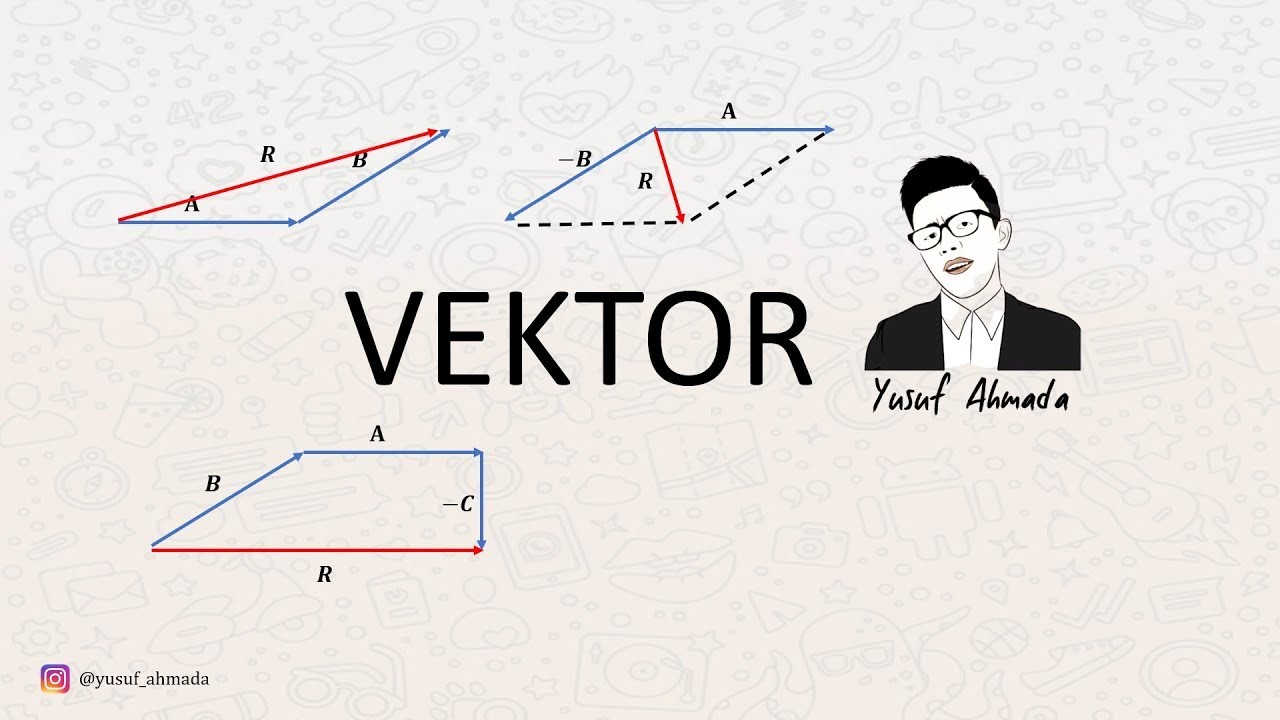
- 📝 Vectors are represented by arrows to indicate direction and can be manipulated using the 'head-tail' technique or the 'parallelogram method' for addition.
- 🔍 The concept of negative vectors is explored, showing that subtracting a vector from itself results in zero, and that a negative vector is the original vector flipped 180 degrees.
- ⚖️ Vector subtraction is explained as being equivalent to adding a negative vector, which can be visualized using both the head-tail technique and the parallelogram technique.
- 📊 The magnitude of a vector is calculated as the square root of the sum of the squares of its components, and the angles with the axes (theta and phi) are used to decompose a vector into its components.
- 📐 Unit vectors are introduced as vectors with a magnitude of one that point in the direction of the positive axes, and are used to express vectors in terms of their components along the axes.
- ✖️ The dot product of two vectors is defined as a scalar resulting from the sum of the products of their corresponding components or as the product of the magnitudes and the cosine of the angle between them.
- ✂️ The cross product, or vector product, is introduced as a method to multiply vectors resulting in another vector perpendicular to the plane containing the original vectors, with direction determined by the right-hand rule.
- 🔄 The motion of a particle in three-dimensional space is described by decomposing its position, velocity, and acceleration into components along the x, y, and z axes, allowing for the analysis of complex motion as a combination of independent one-dimensional motions.
- 🚀 The independence of motion in the x and y directions is demonstrated through projectile motion, where the horizontal velocity remains constant while the vertical motion is influenced by gravity.
- 🎯 An experiment is proposed to launch a golf ball with a horizontal velocity matching that of a moving cart to illustrate the principle that the horizontal motion is independent of the vertical motion influenced by gravity.
Q & A
What is the main topic discussed in the provided script?
-The main topic discussed in the script is the concept of vectors in physics, including their addition, subtraction, and multiplication (dot and cross products), as well as their applications in motion and forces.
What is a scalar in physics?
-A scalar in physics is a quantity that is determined by a single number and has no direction, such as mass, temperature, and speed.
How is a vector represented?
-A vector is represented by an arrow, where the length of the arrow indicates the magnitude and the direction of the arrow indicates the direction of the vector.
What are the two common methods for adding vectors?
-The two common methods for adding vectors are the 'head-tail' technique and the 'parallelogram method'.
What is the significance of the negative vector in the context of vector subtraction?
-The negative vector is significant in vector subtraction because it represents the vector that, when added to a given vector, results in a zero vector. It is essentially the original vector flipped over 180 degrees.
What is the dot product of two vectors?
-The dot product of two vectors is a scalar value obtained by multiplying corresponding components of the vectors and summing the results. It can also be represented as the product of the magnitudes of the two vectors and the cosine of the angle between them.
What is the cross product of two vectors?
-The cross product of two vectors results in a vector that is perpendicular to both of the original vectors. It is calculated using a determinant involving the unit vectors and components of the original vectors.
How does the magnitude of a vector relate to its components?
-The magnitude of a vector is the square root of the sum of the squares of its components along each axis (Ax^2 + Ay^2 + Az^2)^(1/2).
What is the physical interpretation of the dot product being zero?
-A dot product of zero indicates that the two vectors are perpendicular to each other, as the cosine of the angle between them (90 degrees) is zero.
How can the motion of a particle in three-dimensional space be decomposed?
-The motion of a particle in three-dimensional space can be decomposed into three independent one-dimensional motions along the x, y, and z axes, each with its own position, velocity, and acceleration components.
What is the practical demonstration mentioned in the script to illustrate the independent behavior of motion in the x and y directions?
-The practical demonstration involves shooting a golf ball with a horizontal velocity that matches the motion of a moving cart, showing that the ball maintains a constant horizontal velocity while the cart moves underneath it.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahora5.0 / 5 (0 votes)